I den senaste handledningen diskuterade vi kort om filter. I den här handledningen kommer vi att diskutera dem grundligt. Innan vi diskuterar om låt oss först prata om masker. Begreppet mask har diskuterats i vår handledning om konvolution och masker.

Blurring masks vs derivative masks

Vi kommer att utföra en jämförelse mellan blurring masks och derivative masks.

Blurring masks

En blurring mask har följande egenskaper.

• Alla värden i suddarmasker är positiva
• Summan av alla värden är lika med 1
• Kantinnehållet minskas genom att använda en suddarmask
• När storleken på masken växer kommer mer utjämningseffekt att ske

Derivativa masker

En derivativ mask har följande egenskaper.

• En derivativ mask har positiva och såväl som negativa värden
• Summan av alla värden i en derivativ mask är lika med noll
• Kantinnehållet ökas av en derivativ mask
• När storleken på masken växer , ökas mer kantinnehåll

Samband mellan oskärpningsmasker och derivativa masker med högpassfilter och lågpassfilter.

Sambandet mellan suddig mask och avledd mask med högpassfilter och lågpassfilter kan enkelt definieras som följande:

• Suddig masker kallas också för lågpassfilter
• Avledda masker kallas också för högpassfilter

Högpassfrekvenskomponenter och lågpassfrekvenskomponenter

Högpassfrekvenskomponenterna anger kanter medan lågpassfrekvenskomponenterna anger släta områden.

Ideala lågpassfilter och ideala högpassfilter

Detta är det vanligaste exemplet på lågpassfilter.

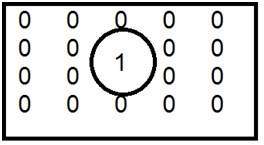
När ett placeras inuti och nollan placeras utanför , får vi en suddig bild. När vi nu ökar storleken på 1 skulle oskärpan öka och kantinnehållet minska.

Detta är ett vanligt exempel på högpassfilter.

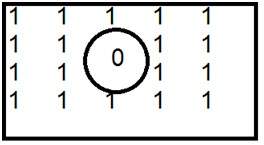
När 0 placeras innanför får vi kanter, vilket ger oss en skissad bild. Ett idealiskt lågpassfilter i frekvensdomänen ges nedan.

Det ideala lågpassfiltret kan grafiskt representeras som

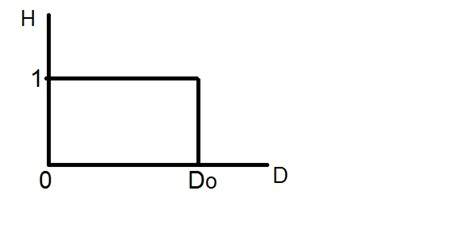
Nu tillämpar vi detta filter på en verklig bild och ser vad vi får.

Provbild

Bild i frekvensdomän

Användning av filter över denna bild

Resultatbild

Med samma sätt kan ett idealiskt högpassfilter tillämpas på en bild. Men uppenbarligen skulle resultaten bli olika eftersom, lågpasset minskar det kantiga innehållet och högpasset ökar det.

Gaussianskt lågpass och Gaussiskt högpassfilter

Gaussianskt lågpass och Gaussiskt högpassfilter minimerar det problem som uppstår i ideala lågpass- och högpassfilter.

Detta problem är känt som ringningseffekt. Detta beror på att övergången mellan en färg och en annan i vissa punkter inte kan definieras exakt, vilket gör att ringningseffekten uppträder i den punkten.

Klipp på den här grafen.

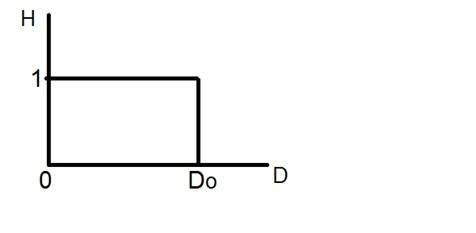
Detta är en representation av det ideala lågpassfiltret. Vid den exakta punkten för Do kan du inte säga att värdet skulle vara 0 eller 1. På grund av vilket ringningseffekten uppträder vid den punkten.

För att minska effekten som uppträder är idealiskt lågpass och idealiskt högpassfilter införs följande Gaussiskt lågpassfilter och Gaussiskt högpassfilter.

Gaussianskt lågpassfilter

Konceptet för filtrering och lågpass förblir detsamma, men det är bara övergången som blir annorlunda och blir mer jämn.

Det gaussiska lågpassfiltret kan representeras som

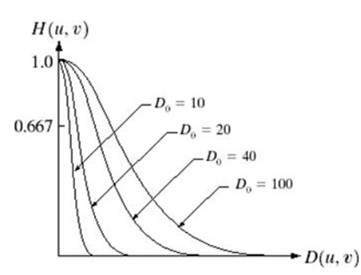
Bemärk den mjuka kurvaövergången, på grund av vilken vid varje punkt värdet på Do, kan definieras exakt.

Gaussianskt högpassfilter

Gaussianskt högpassfilter har samma koncept som det ideala högpassfiltret, men återigen är övergången jämnare jämfört med det ideala.