Un domeniu de interes din ce în ce mai mare pentru oamenii de știință care explorează importanța, puterea sau influența între entități se numește teoria grafurilor. Rădăcinile teoriei grafurilor au început în 1736, când matematicianul Carl Ehler i-a prezentat lui Leonhard Euler problema podurilor din Konigsberg.
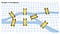
Problema podurilor din Konigsberg se bazează pe fostul oraș german Konigsberg, care se află pe ambele maluri ale râului Pregel. În centru, existau două insule mari care erau conectate între ele și cu malurile râului prin șapte poduri. Carl Ehler a devenit obsedat de găsirea unui traseu care să treacă prin fiecare dintre cele șapte poduri fără a trece de mai multe ori peste vreunul dintre ele. Ehler a luat legătura cu Leonhard Euler, un matematician elvețian. Euler a confirmat ipoteza lui Ehler că problema nu avea o soluție, iar explicația lui Euler a informat o nouă paradigmă matematică numită Geometria poziției.
Noua paradigmă de geometrie a lui Euler a afirmat că locația podurilor nu conta. În schimb, problema poate fi simplificată prin transformarea fiecărui pod într-un punct (nod) cu linii (muchii) care să reprezinte legăturile dintre ele. Această practică de a folosi noduri și muchii este acum cunoscută sub numele de Teoria Grafurilor.
Puteți citi mai multe despre problema Podurilor din Konigsberg aici.
Inițial, Teoria Grafurilor nu a servit prea mult în rezolvarea problemelor și nu a fost foarte apreciată de matematicieni. Cu toate acestea, puterea de calcul modernă pentru a procesa permutări mari a făcut ca principiile teoriei grafurilor să devină mai practice. Acest articol vă învață să aplicați principiile Teoriei Grafurilor la analiza bazată pe Python.


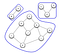
Nu toate rețelele dintr-un sistem Graf sunt interconectate. Această deconectare are loc atunci când se formează componentele. După cum se arată în graficul de mai jos, o componentă este formată numai atunci când fiecare nod are o cale către alte noduri.
Teorie aplicată a grafurilor în Python
În Python, networkx este adesea folosit pentru teoria aplicată a grafurilor, cunoscută și sub numele de analiza rețelelor . Pachetul are o funcționalitate utilă pentru a rezuma rapid caracteristicile unui graf. Puteți revizui pașii de mai jos și să ne urmăriți pe măsură ce creăm un graf și înțelegem componența sa.
Primul cod de mai jos creează un obiect gol de graf P. Următorii pași adaugă noduri și descriu marginile.
Argumente precum <object>.nodes() sau <object>.edges() sunt modalități rapide de a vizualiza toate nodurile și marginile sistemului de grafuri.
print(P.nodes())print(P.edges())
În cele din urmă, nx.draw este utilizat pentru a vizualiza rețeaua.
%matplotlib inline
import matplotlib.pyplot as plt
nx.draw(P, with_labels = True)
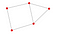
Exerciții 1:
Acum că au fost discutate conceptele de bază ale grafurilor, următoarele exerciții sunt o metodă bună de a exersa:
- Câte noduri sunt în graful de mai sus?
- Câte muchii sunt în graficul de mai sus?
- Care este geodezica pentru E și C?
- Există mai mult de 1 componentă în grafic?
Utilizarea datelor reale
Exercițiul de mai jos va folosi date pentru zborurile în Statele Unite în 2015. Setul de date include aeroporturile de origine și de destinație, pe lângă atributele care descriu zborul, inclusiv timpul de zbor și întârzierile (legate de condițiile meteorologice, de securitate sau de compania aeriană).
Pentru că setul de date este mare, exercițiul se va concentra pe zborurile care provin de pe aeroporturile din zona Los Angeles (Los Angeles (LAX), Burbank (BUR), Orange County (SNA) și San Bernardino County (ONT)). În plus, accentul va fi pus pe revizuirea zborurilor care se aseamănă cu programul meu de călătorie la Deloitte – zboruri care pleacă duminica și se întorc joia.
Din moment ce avem deja date de origine și destinație, câmpurile **** ORIGIN_AIRPORT și DESTINATION_AIRPORT vor servi drept câmpuri sursă pentru noduri și muchii – nu este nevoie să creăm noduri sau muchii așa cum am făcut în primul exercițiu. Odată ce nodurile sunt definite, <object>.edges() va furniza toate relațiile de pereche dintre ele. În cele din urmă, nx.draw va ajuta la producerea unui grafic pentru muchii.

FG.edges()

nx.draw(FG, with_labels = True)

În rezultatul de mai sus, nodurile sunt etichetate cu codurile de aeroport. Toate marginile duc la unul dintre cele patru aeroporturi din zona Los Angeles, deoarece acestea patru au fost singurele selectate pentru acest exercițiu. Los Angeles International (LAX) este cel mai mare aeroport dintre cele patru, iar graficul arată în mod clar că multe orașe sunt accesibile doar de la LAX și nu și de la alte aeroporturi mai mici. Acest lucru evidențiază conectivitatea, sau gradul de centralitate, al LAX-ului. În networkx, nx.algorithms.degree_centrality(<object>) ****este folosit pentru a găsi centralitatea fiecărui nod în sistemul de grafuri.
# Calculating the centrality of each of the airports
nx.algorithms.degree_centrality(FG)
Pot fi mai granular și putem folosi un scurt „for loop” pentru a produce muchii între două zone de interes. De exemplu, următorul cod este folosit pentru a găsi toate zborurile posibile din comitatul San Bernardino (ONT) către Newark (EWR) fie duminică, fie joi.
Printre cele câteva opțiuni de zbor între comitatul San Bernardino și Newark, nx.dijkstra_path poate fi folosit pentru a găsi calea euclidiană (sau calea cea mai scurtă).
#Finding the dijkstra path
djk_path = nx.dijkstra_path(FG, source='ONT', target='EWR')
djk_path
Exerciții 2:
- Produceți următorul graf folosind
nx.draw(). Notă: este posibil ca rețeaua dvs. să nu arate exact la fel, dar căile, marginile și nodurile ar trebui să se potrivească cu rețeaua de mai jos. - Imprimați toate marginile.
- Care este cea mai scurtă cale de la L la F?

.