În ultimul tutorial, am discutat pe scurt despre filtre. În acest tutorial vom discuta amănunțit despre ele. Înainte de a discuta despre haideți să vorbim mai întâi despre măști. Conceptul de mască a fost discutat în tutorialul nostru despre convoluție și măști.

Măști de estompare vs măști derivate

Vom efectua o comparație între măștile de estompare și măștile derivate.

Măști de estompare

O mască de estompare are următoarele proprietăți.

• Toate valorile din măștile de estompare sunt pozitive
• Suma tuturor valorilor este egală cu 1
• Contenutul marginilor este redus prin utilizarea unei măști de estompare
• Cu cât dimensiunea măștii crește, cu atât mai mult va avea loc efectul de netezire

Mastile derivate

O mască derivată are următoarele proprietăți.

• O mască derivată are valori pozitive și, de asemenea, negative
• Suma tuturor valorilor dintr-o mască derivată este egală cu zero
• Conținutul marginilor este mărit de o mască derivată
• Pe măsură ce dimensiunea măștii crește , se mărește mai mult conținutul marginilor

Relația dintre masca de estompare și masca derivată cu filtre trece înalt și filtre trece-jos.

Relația dintre masca de estompare și masca derivată cu un filtru de trecere înaltă și un filtru de trecere joasă poate fi definită simplu astfel:

• Masca de estompare se mai numește și filtru de trecere joasă
• Masca derivată se mai numește și filtru de trecere înaltă

Componente de frecvență de trecere înaltă și componente de frecvență de trecere joasă

Componentele de frecvență de trecere înaltă denotă marginile, în timp ce componentele de frecvență de trecere joasă denotă regiunile netede.

Filtrele low pass ideale și filtrele High pass ideale

Acesta este exemplul obișnuit de filtru low pass.

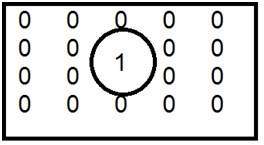
Când unu este plasat înăuntru și zero este plasat afară , obținem o imagine neclară. Acum, pe măsură ce creștem dimensiunea lui 1, încețoșarea va crește și conținutul marginilor va fi redus.

Acesta este un exemplu obișnuit de filtru trece înalt.

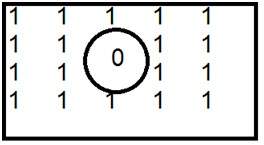
Când 0 este plasat în interior, obținem margini, ceea ce ne dă o imagine schițată. Un filtru low pass ideal în domeniul frecvenței este dat mai jos.

Filtrul low pass ideal poate fi reprezentat grafic ca

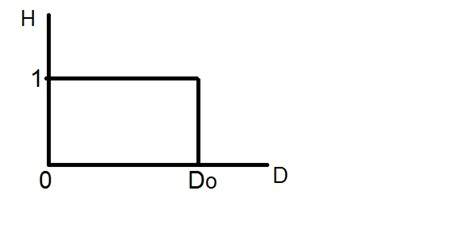
Acum să aplicăm acest filtru la o imagine reală și să vedem ce am obținut.

Imaginea de probă

Imaginea în domeniul frecvenței

Aplicarea filtrului peste această imagine

Imaginea rezultată

În același mod, un filtru trece înalt ideal poate fi aplicat pe o imagine. Dar, în mod evident, rezultatele vor fi diferite, deoarece filtrul low pass reduce conținutul marginilor, iar filtrul high pass îl mărește.

Filtrele Gaussian Low pass și Gaussian High pass

Filtrele Gaussian Low pass și Gaussian High pass minimizează problema care apare în cazul filtrelor low pass și high pass ideale.

Această problemă este cunoscută sub numele de efect de inelare. Acest lucru se datorează faptului că în anumite puncte tranziția dintre o culoare și alta nu poate fi definită cu precizie, fapt pentru care apare efectul de inelare în acel punct.

Aruncă o privire la acest grafic.

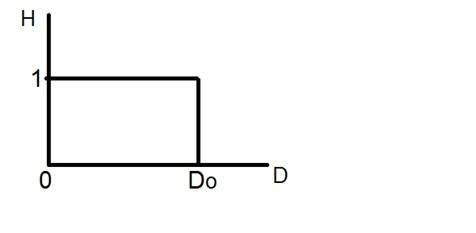
Aceasta este reprezentarea filtrului low pass ideal. Acum, în punctul exact al lui Do, nu se poate spune că valoarea ar fi 0 sau 1. Din cauza căreia apare efectul de inelare în acel punct.

Atunci, pentru a reduce efectul care apare este filtrul trece-jos ideal și filtrul trece-înalt ideal, se introduce următorul filtru trece-jos gaussian și filtrul trece-înalt gaussian.

Filtrul trece-jos gaussian

Conceptul de filtrare și trece-jos rămâne același, dar numai tranziția devine diferită și devine mai lină.

Filtrul Gaussian low pass poate fi reprezentat ca

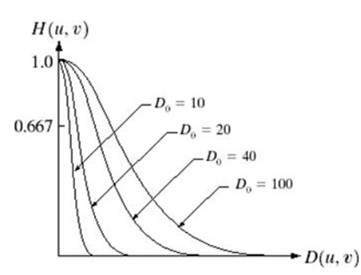
Rețineți tranziția lină a curbei, datorită căreia, în fiecare punct, valoarea lui Do, poate fi definită cu exactitate.

Filtrul trece-înalt gaussian

Filtrul trece-înalt gaussian are același concept ca și filtrul trece-înalt ideal, dar, din nou, tranziția este mai lină în comparație cu cea ideală.

.