W ostatnim tutorialu, krótko omówiliśmy filtry. W tym tutorialu omówimy je dokładnie. Zanim przejdziemy do omówienia filtrów, porozmawiajmy najpierw o maskach. Pojęcie maski zostało omówione w naszym samouczku dotyczącym konwolucji i masek.

Maski rozmywające vs maski pochodne

Przeprowadzimy porównanie pomiędzy maskami rozmywającymi a maskami pochodnymi.

Maski rozmywające

Maska rozmywająca ma następujące właściwości.

• Wszystkie wartości w maskach rozmywających są dodatnie
• Suma wszystkich wartości jest równa 1
• Zawartość krawędzi jest redukowana przez użycie maski rozmywającej
• Wraz ze wzrostem rozmiaru maski nastąpi większy efekt wygładzania

Maski pochodne

Maska pochodna ma następujące właściwości.

• Maska pochodna ma wartości dodatnie, jak również ujemne
• Suma wszystkich wartości w masce pochodnej jest równa zeru
• Zawartość krawędzi jest zwiększana przez maskę pochodną
• Wraz ze wzrostem rozmiaru maski zwiększa się zawartość krawędzi

Zależność między maską rozmywającą a maską pochodną z filtrami górnoprzepustowymi i dolnoprzepustowymi.

Zależność między maską rozmywającą i maską pochodną z filtrem górnoprzepustowym i filtrem dolnoprzepustowym można zdefiniować w prosty sposób jako.

• Maski rozmywające są również nazywane filtrem dolnoprzepustowym
• Maski pochodne są również nazywane filtrem górnoprzepustowym

Składowe częstotliwości górnoprzepustowe i składowe częstotliwości dolnoprzepustowe

Składowe częstotliwości górnoprzepustowe oznaczają krawędzie, natomiast składowe częstotliwości dolnoprzepustowe oznaczają gładkie regiony.

Idealne filtry dolnoprzepustowe i idealne filtry górnoprzepustowe

To jest wspólny przykład filtru dolnoprzepustowego.

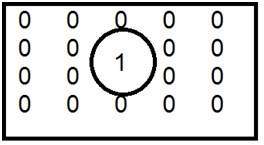
Gdy jedynka jest umieszczona wewnątrz, a zero na zewnątrz, otrzymujemy rozmazany obraz. Teraz, gdy zwiększamy rozmiar 1, rozmycie będzie zwiększone, a zawartość krawędzi będzie zmniejszona.

Jest to powszechny przykład filtru górnoprzepustowego.

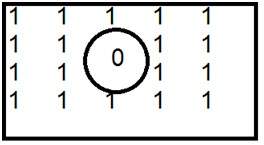
Gdy 0 jest umieszczone wewnątrz, otrzymujemy krawędzie, co daje nam naszkicowany obraz. Idealny filtr dolnoprzepustowy w dziedzinie częstotliwości jest podany poniżej.

Idealny filtr dolnoprzepustowy można przedstawić graficznie jako

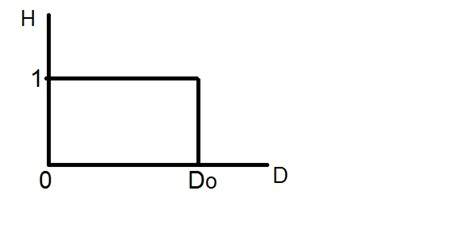
Teraz zastosujmy ten filtr do rzeczywistego obrazu i zobaczmy, co uzyskaliśmy.

Przykładowy obraz

Obraz w dziedzinie częstotliwości

Zastosowanie filtru na tym obrazie

Obraz wynikowy

W ten sam sposób, idealny filtr górnoprzepustowy może być zastosowany na obrazie. Ale oczywiście wyniki będą inne, ponieważ filtr dolnoprzepustowy zmniejsza zawartość krawędzi, a górnoprzepustowy ją zwiększa.

Gaussian Low Pass and Gaussian High Pass filter

Gaussian low pass and Gaussian high pass filter minimalizują problem, który występuje w idealnym filtrze dolnoprzepustowym i górnoprzepustowym.

Problem ten jest znany jako efekt dzwonienia. Wynika to z powodu, ponieważ w niektórych punktach przejście między jednym kolorem a drugim nie może być dokładnie zdefiniowane, z powodu czego efekt dzwonienia pojawia się w tym punkcie.

Spójrz na ten wykres.

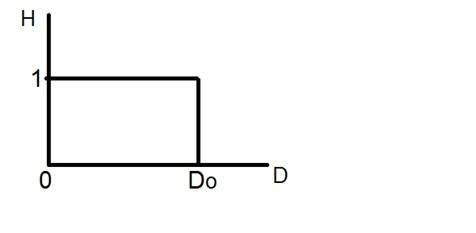
To jest reprezentacja idealnego filtra dolnoprzepustowego. Teraz w dokładnym punkcie Do, nie można powiedzieć, że wartość będzie 0 lub 1. Ze względu na które efekt dzwonienia pojawia się w tym punkcie.

Więc w celu zmniejszenia efektu, który pojawia się jest idealny filtr dolnoprzepustowy i idealny filtr górnoprzepustowy, następujące Gaussian filtr dolnoprzepustowy i Gaussian filtr górnoprzepustowy jest wprowadzony.

Gaussian Filtr dolnoprzepustowy

Koncepcja filtrowania i dolnoprzepustowy pozostaje taka sama, ale tylko przejście staje się inna i stają się bardziej gładkie.

Gaussian filtr dolnoprzepustowy może być reprezentowany jako

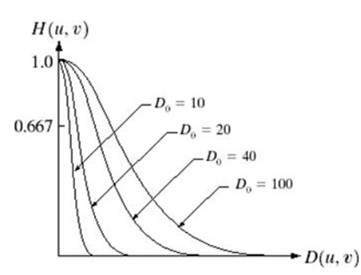
Zauważ gładkie przejście krzywej, dzięki czemu w każdym punkcie, wartość Do, może być dokładnie określona.

Gaussowski filtr górnoprzepustowy

Gaussowski filtr górnoprzepustowy ma taką samą koncepcję jak idealny filtr górnoprzepustowy, ale ponownie przejście jest bardziej gładkie w porównaniu z idealnym.