In de vorige tutorial hebben we het kort gehad over filters. In deze tutorial gaan we er dieper op in. Laten we het eerst hebben over maskers. Het concept van maskers is besproken in onze tutorial over convolutie en maskers.

Vermagende maskers vs afgeleide maskers

We gaan een vergelijking uitvoeren tussen vervagende maskers en afgeleide maskers.

Vermagende maskers

Een vervagend masker heeft de volgende eigenschappen.

• Alle waarden in vervagende maskers zijn positief
• De som van alle waarden is gelijk aan 1
• De randinhoud wordt verminderd door het gebruik van een vervagend masker
• Als de grootte van het masker groeit, zal er meer afvlakkingseffect plaatsvinden

Afgeleide maskers

Een afgeleide masker heeft de volgende eigenschappen.

• Een afgeleid masker heeft zowel positieve als negatieve waarden
• De som van alle waarden in een afgeleid masker is gelijk aan nul
• De randinhoud wordt verhoogd door een afgeleid masker
• Als de grootte van het masker groeit , wordt meer randinhoud verhoogd

Relatie tussen vervagend masker en afgeleid masker met hoogdoorlaatfilters en laagdoorlaatfilters.

De relatie tussen vervagend masker en afgeleide masker met een hoogdoorlaatfilter en een laagdoorlaatfilter kan eenvoudig worden gedefinieerd als.

• Vervagende maskers worden ook wel aangeduid als laagdoorlaatfilter
• Afgeleide maskers worden ook wel aangeduid als hoogdoorlaatfilter

Hoogdoorlaatfrequentiecomponenten en laagdoorlaatfrequentiecomponenten

De hoogdoorlaatfrequentiecomponenten duiden op randen terwijl de laagdoorlaatfrequentiecomponenten duiden op gladde gebieden.

Ideale laagdoorlaat- en ideale hoogdoorlaatfilters

Dit is het gebruikelijke voorbeeld van een laagdoorlaatfilter.

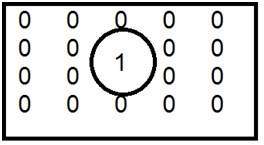
Wanneer één binnen en nul buiten wordt geplaatst, krijgen we een onscherp beeld. Als we nu de grootte van 1 vergroten, neemt de onscherpte toe en wordt de randinhoud kleiner.

Dit is een veelvoorkomend voorbeeld van een hoogdoorlaatfilter.

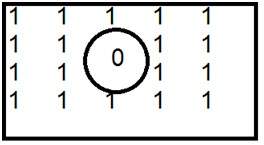
Als 0 binnen wordt geplaatst, krijgen we randen, waardoor we een geschetst beeld krijgen. Een ideaal laagdoorlaatfilter in het frequentiedomein is hieronder gegeven.

Het ideale laagdoorlaatfilter kan grafisch worden weergegeven als

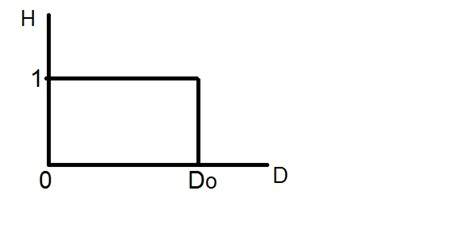
Nu passen we dit filter toe op een echte afbeelding en laten we eens kijken wat we krijgen.

Staalafbeelding

Afbeelding in frequentiedomein

Aanbrengen filter op deze afbeelding

Resultaat afbeelding

Op dezelfde manier kan een ideaal high pass filter op een afbeelding worden toegepast. Maar de resultaten zouden natuurlijk verschillend zijn, omdat de laagdoorlaat de randen vermindert en de hoogdoorlaat ze verhoogt.

Gaussisch laagdoorlaat- en Gaussisch hoogdoorlaatfilter

Gaussisch laagdoorlaat- en Gaussisch hoogdoorlaatfilter minimaliseren het probleem dat zich voordoet bij het ideale laagdoorlaat- en hoogdoorlaatfilter.

Dit probleem staat bekend als het ringeffect. Dit komt doordat op sommige punten de overgang van de ene kleur naar de andere niet precies kan worden bepaald, waardoor op dat punt het ringeffect optreedt.

Bekijkt u deze grafiek eens.

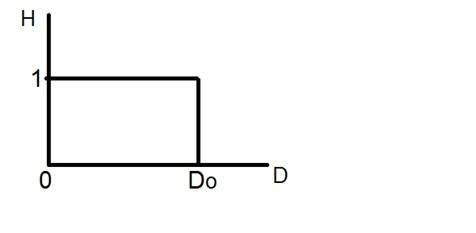
Dit is de weergave van het ideale laagdoorlaatfilter. Nu kun je op het exacte punt van Do niet zeggen of de waarde 0 of 1 zou zijn. Waardoor de ringing effect verschijnt op dat punt.

Dus om het effect dat verschijnt is ideaal laagdoorlaatfilter en ideaal hoogdoorlaatfilter te verminderen, wordt de volgende Gaussian laagdoorlaatfilter en Gaussian hoogdoorlaatfilter geïntroduceerd.

Gaussian laagdoorlaatfilter

Het concept van filtering en laagdoorlaat blijft hetzelfde, maar alleen de overgang wordt anders en wordt meer glad.

Het Gaussische laagdoorlaatfilter kan worden voorgesteld als

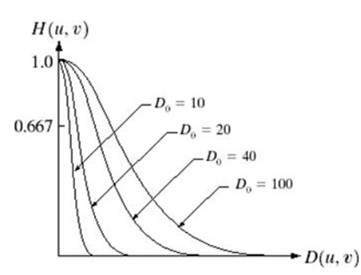
Merk de vloeiende overgang van de curve op, waardoor op elk punt de waarde van Do precies kan worden bepaald.

Gaussisch hoogdoorlaatfilter

Gaussisch hoogdoorlaatfilter heeft hetzelfde concept als het ideale hoogdoorlaatfilter, maar ook hier is de overgang vloeiender in vergelijking met het ideale.