Nell’ultimo tutorial, abbiamo parlato brevemente dei filtri. In questo tutorial ne parleremo approfonditamente. Prima di discuterne, parliamo prima delle maschere. Il concetto di maschera è stato discusso nel nostro tutorial su convoluzione e maschere.

Maschere sfocanti vs maschere derivate

Eseguiremo un confronto tra maschere sfocanti e maschere derivate.

Maschere sfocanti

Una maschera sfocante ha le seguenti proprietà.

• Tutti i valori nelle maschere di sfocatura sono positivi
• La somma di tutti i valori è uguale a 1
• Il contenuto del bordo è ridotto usando una maschera di sfocatura
• Come la dimensione della maschera cresce, più effetto di levigatura avrà luogo

Maschere derivate

Una maschera derivata ha le seguenti proprietà.

• Una maschera derivativa ha valori positivi e negativi
• La somma di tutti i valori in una maschera derivativa è uguale a zero
• Il contenuto del bordo è aumentato da una maschera derivativa
• Come la dimensione della maschera cresce, più contenuto del bordo è aumentato

Relazione tra maschera di sfocatura e maschera derivativa con filtri passa alto e passa basso.

La relazione tra la maschera di sfocatura e la maschera derivata con un filtro passa alto e un filtro passa basso può essere definita semplicemente come.

• Le maschere di sfocatura sono anche chiamate come filtro passa basso
• Le maschere derivate sono anche chiamate come filtro passa alto

Componenti di frequenza passa alto e componenti di frequenza passa basso

Le componenti di frequenza passa alto denotano bordi mentre le componenti di frequenza passa basso denotano regioni lisce.

Filtri passa basso ideali e filtri passa alto ideali

Questo è l’esempio comune di filtro passa basso.

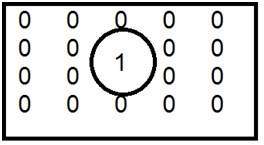
Quando uno è posto all’interno e lo zero è posto all’esterno, abbiamo un’immagine sfocata. Ora, quando aumentiamo la dimensione di 1, la sfocatura sarebbe aumentata e il contenuto del bordo sarebbe stato ridotto.

Questo è un esempio comune di filtro passa alto.

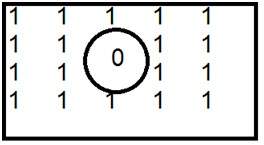
Quando lo 0 è posto all’interno, otteniamo dei bordi, che ci danno un’immagine abbozzata. Un filtro passa-basso ideale nel dominio della frequenza è dato qui sotto.

Il filtro passa-basso ideale può essere rappresentato graficamente come

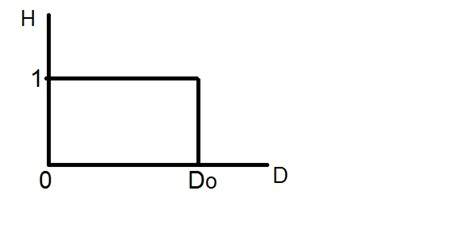
Applichiamo ora questo filtro a un’immagine reale e vediamo cosa abbiamo ottenuto.

Immagine campione

Immagine nel dominio della frequenza

Applicazione del filtro su questa immagine

Immagine risultante

Con lo stesso metodo, un filtro passa alto ideale può essere applicato su un’immagine. Ma ovviamente i risultati sarebbero diversi, perché il passa basso riduce il contenuto bordato e il passa alto lo aumenta.

Filtro passa basso gaussiano e filtro passa alto gaussiano

Il filtro passa basso gaussiano e il filtro passa alto gaussiano minimizzano il problema che si verifica nei filtri passa basso e passa alto ideali.

Questo problema è conosciuto come effetto ringing. Ciò è dovuto al fatto che in alcuni punti la transizione tra un colore e l’altro non può essere definita con precisione, per cui l’effetto ringing appare in quel punto.

Guardate questo grafico.

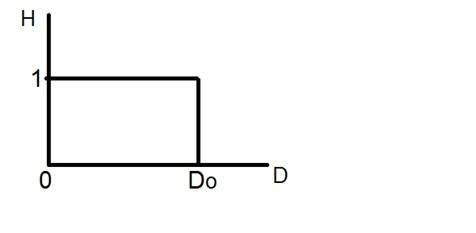
Questa è la rappresentazione del filtro passa basso ideale. Ora, nel punto esatto di Do, non si può dire che il valore sarebbe 0 o 1. A causa del quale l’effetto ringing appare in quel punto.

Quindi, al fine di ridurre l’effetto che appare è il filtro passa basso ideale e il filtro passa alto ideale, viene introdotto il seguente filtro passa basso gaussiano e filtro passa alto gaussiano.

Filtro passa basso gaussiano

Il concetto di filtraggio e passa basso rimane lo stesso, ma solo la transizione diventa diversa e diventa più regolare.

Il filtro passa basso gaussiano può essere rappresentato come

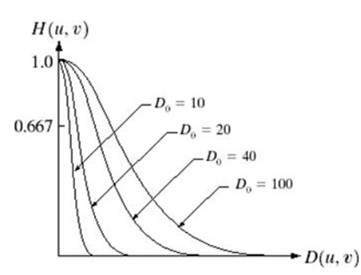
Nota la transizione liscia della curva, grazie alla quale in ogni punto, il valore di Do, può essere definito esattamente.

Filtro passa alto gaussiano

Il filtro passa alto gaussiano ha lo stesso concetto del filtro passa alto ideale, ma di nuovo la transizione è più regolare rispetto a quella ideale.