A legutóbbi bemutatóban a szűrőkről beszéltünk röviden. Ebben a bemutatóban alaposan kitérünk rájuk. Mielőtt beszélnénk róluk, beszéljünk először a maszkokról. A maszk fogalmát már tárgyaltuk a konvolúció és maszkok oktatóanyagunkban.

Homályosító maszkok vs. deriváló maszkok

Egy összehasonlítást fogunk végezni a homályosító maszkok és a deriváló maszkok között.

Homályosító maszkok

A homályosító maszk a következő tulajdonságokkal rendelkezik.

• Az elmosó maszkok minden értéke pozitív
• Az összes érték összege egyenlő 1-gyel
• Az éltartalom csökken az elmosó maszk használatával
• Amint a maszk mérete nő, annál nagyobb simító hatás érvényesül

Deriváló maszkok

A deriváló maszk a következő tulajdonságokkal rendelkezik.

• Egy derivált maszknak pozitív és negatív értékei is vannak
• A derivált maszkban az összes érték összege egyenlő nullával
• Az éltartalmat növeli a derivált maszk
• Amint nő a maszk mérete , több éltartalom növekszik

Az elmosó maszk és a derivált maszk közötti összefüggés magas- és mélyszűrőkkel.

Az elmosó maszk és a származtatott maszk közötti kapcsolat magas- és aluláteresztő szűrővel egyszerűen meghatározható.

• Az elmosó maszkokat aluláteresztő szűrőnek is nevezik
• A származtatott maszkokat felüláteresztő szűrőnek is nevezik

Magas- és aluláteresztő frekvencia komponensek

A magasfrekvencia komponensek éleket, míg az aluláteresztő frekvencia komponensek sima területeket jelölnek.

Ideális aluláteresztő és ideális felüláteresztő szűrő

Ez az aluláteresztő szűrő általános példája.

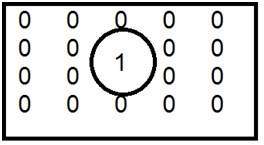
Ha az egyest belülre, a nullát pedig kívülre helyezzük , elmosódott képet kapunk. Most, ahogy növeljük az 1-es méretét, az elmosódás növekedne és az éltartalom csökkenne.

Ez egy gyakori példa a magasáteresztő szűrőre.

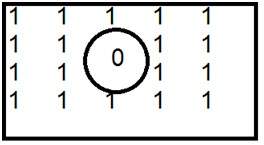
Ha a 0-t belülre helyezzük, éleket kapunk, ami egy vázlatos képet ad. Egy ideális aluláteresztő szűrő frekvenciatartományban az alábbiakban látható.

Az ideális aluláteresztő szűrő grafikusan a következőképpen ábrázolható:

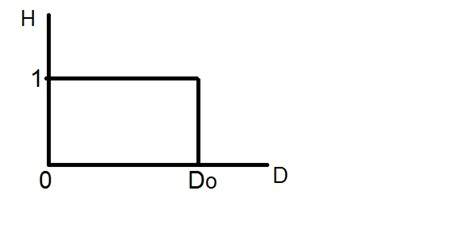
Most alkalmazzuk ezt a szűrőt egy tényleges képre, és lássuk, mit kapunk.

Mintakép

Kép a frekvenciatartományban

A szűrő alkalmazása ezen a képen

Eredménykép

Ezzel a módszerrel egy ideális felüláteresztő szűrő is alkalmazható egy képre. De nyilvánvalóan az eredmények eltérőek lennének, mivel az aluláteresztő csökkenti, a felüláteresztő pedig növeli a peremtartalmat.

Gaussi aluláteresztő és Gauss-féle felüláteresztő szűrő

Az ideális aluláteresztő és felüláteresztő szűrőnél fellépő problémát minimalizálja.

Ezt a problémát gyűrűző hatásnak nevezik. Ennek az az oka, hogy bizonyos pontokon nem lehet pontosan meghatározni az egyik színről a másikra való átmenetet, ami miatt ott megjelenik a gyűrűző hatás.

Nézzük meg ezt a grafikont.

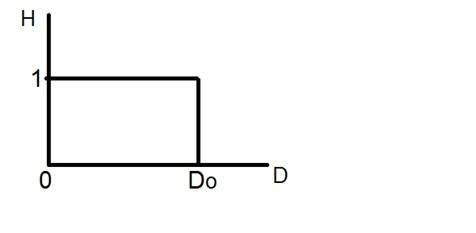
Ez az ideális aluláteresztő szűrő ábrázolása. Most a Do pontos pontjánál nem lehet megmondani, hogy az érték 0 vagy 1 lenne. Emiatt az adott ponton megjelenik a csengő hatás.

Az ideális aluláteresztő és ideális felüláteresztő szűrőnél megjelenő hatás csökkentése érdekében tehát a következő Gauss aluláteresztő szűrő és Gauss felüláteresztő szűrő kerül bevezetésre.

Gauss aluláteresztő szűrő

A szűrés és az aluláteresztő fogalma ugyanaz marad, csak az átmenet változik és simábbá válik.

A Gauss-féle aluláteresztő szűrő a következőképpen ábrázolható

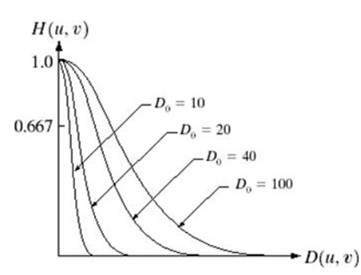
Megfigyelhető a sima görbeátmenet, amelynek köszönhetően minden egyes ponton a Do értéke pontosan meghatározható.

Gauss-féle magasáteresztő szűrő

A Gauss-féle magasáteresztő szűrő ugyanazzal a koncepcióval rendelkezik, mint az ideális magasáteresztő szűrő, de az átmenet ismét simább az ideálishoz képest.