Viimeisessä tutoriaalissa keskustelimme lyhyesti suodattimista. Tässä opetusohjelmassa keskustelemme niistä perusteellisesti. Ennen keskustelua puhutaan ensin maskeista. Maskin käsitettä on käsitelty konvoluutiota ja maskeja käsittelevässä opetusohjelmassamme.

Sumennusmaskit vs. johdannaismaskit

Tehdään vertailu sumennusmaskien ja johdannaismaskien välillä.

Sumennusmaskit

Sumennusmaskilla on seuraavat ominaisuudet.

• Kaikki arvot sumentavissa maskeissa ovat positiivisia
• Kaikkien arvojen summa on yhtä suuri kuin 1
• Reunapitoisuus vähenee käyttämällä sumentavaa maskia
• Mikäli maskin koko kasvaa, sitä enemmän tasoitusvaikutusta tapahtuu

Derivaattorimaskit

Derivaattorimaskilla on seuraavat ominaisuudet.

• Johdannaismaskilla on positiivisia ja sekä negatiivisia arvoja
• Johdannaismaskin kaikkien arvojen summa on yhtä suuri kuin nolla
• Johdannaismaski kasvattaa reunapitoisuutta
• Maskin koon kasvaessa reunapitoisuutta kasvatetaan enemmän

Hämärtymismaskin ja johdannaismaskin välinen suhde korkeapäästösuodattimilla ja alipäästösuodattimilla.

Ylipäästösuodattimella ja alipäästösuodattimella varustetun blurring maskin ja derivaattamaskin välinen suhde voidaan määritellä yksinkertaisesti seuraavasti.

• Sblurring maskia kutsutaan myös alipäästösuodattimeksi
• Derivaattamaskia kutsutaan myös ylipäästösuodattimeksi

Ylipäästötaajuuskomponentit ja alipäästötaajuuskomponentit

Ylipäästötaajuuskomponentit merkitsevät särmiä, kun taas alipäästötaajuuskomponentit tarkoittavat sileitä alueita.

Ideaalinen alipäästösuodatin ja ideaalinen ylipäästösuodatin

Tämä on yleinen esimerkki alipäästösuodattimesta.

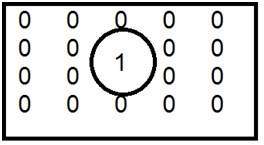
Kun ykkönen sijoitetaan sisälle ja nolla ulkopuolelle , saamme epätarkan kuvan. Nyt kun kasvatamme ykkösen kokoa, sumeus lisääntyisi ja reunapitoisuus vähenisi.

Tämä on yleinen esimerkki korkeapäästösuodattimesta.

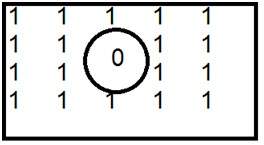
Kun nolla sijoitetaan sisäpuolelle, saamme reunoja, jolloin saamme hahmotellun kuvan. Alla on esitetty ihanteellinen alipäästösuodatin taajuusalueella.

Ideaalinen alipäästösuodatin voidaan esittää graafisesti muodossa

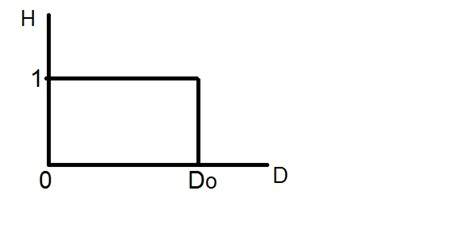
Sovelletaan nyt tätä suodatinta todelliseen kuvaan ja katsotaan, mitä saamme.

Näytekuva

Kuva taajuusalueella

Sovelletaan suodatinta tähän kuvaan

Tuloksena oleva kuva

Samalla samalla tavalla ideaalista korkeapäästösuodatinta voidaan soveltaa kuvaan. Mutta ilmeisesti tulokset olisivat erilaiset, sillä alipäästö vähentää reunimmaista sisältöä ja ylipäästö lisää sitä.

Gaussin alipäästö- ja Gaussin ylipäästösuodatin

Gaussin alipäästö- ja Gaussin ylipäästösuodatin minimoivat ongelman, joka esiintyy ihanteellisessa alipäästö- ja ylipäästösuodattimessa.

Tämä ongelma tunnetaan nimellä ringing-ilmiö. Tämä johtuu siitä syystä, että joissakin kohdissa värin ja toisen värin välistä siirtymää ei voida määritellä tarkasti, minkä vuoksi kyseisessä kohdassa esiintyy rengastusilmiö.

Katsokaa tätä kuvaajaa.

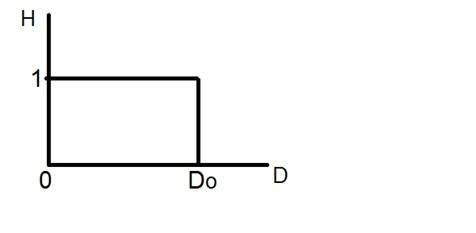
Tämä on ideaalisen alipäästösuodattimen esitys. Nyt tarkassa kohdassa Do ei voi sanoa, että arvo olisi 0 tai 1. Josta johtuen kyseisessä kohdassa esiintyy sointuva vaikutus.

Siten ihanteellinen alipäästö- ja ihanteellinen ylipäästösuodatin on ihanteellinen alipäästö- ja ylipäästösuodatin, joten vaikutuksen vähentämiseksi, joka esiintyy, otetaan käyttöön seuraava Gaussin alipäästösuodatin ja Gaussin ylipäästösuodatin.

Gaussin alipäästösuodatin

Suodatuksen ja alipäästön käsite säilyy samanlaisena, mutta vain siirtyminen muuttuu erilaiseksi ja muuttuu tasaisemmaksi.

Gaussin alipäästösuodatin voidaan esittää

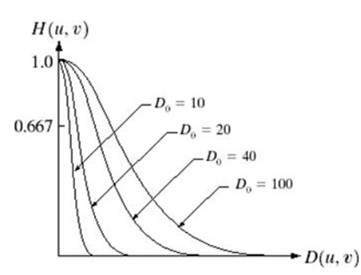
Huomaa tasainen käyrän siirtymä, jonka ansiosta jokaisessa pisteessä Do:n arvo voidaan määritellä tarkasti.

Gaussin korkeapäästösuodatin

Gaussin korkeapäästösuodattimessa on sama käsite kuin ideaalisessa korkeapäästösuodattimessa, mutta jälleen siirtymä on tasaisempi verrattuna ideaaliseen.