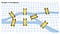
Kigsbergin sillat -ongelma perustuu entiseen saksalaiseen Königsbergin kaupunkiin, joka sijaitsee Pregel-joen molemmin puolin. Keskellä oli kaksi suurta saarta, jotka oli yhdistetty toisiinsa ja jokirantaan seitsemällä sillalla. Carl Ehlerille tuli pakkomielle löytää reitti, jota pitkin voisi kävellä jokaisen seitsemän sillan läpi kävelemättä minkään sillan yli useammin kuin kerran. Ehler otti yhteyttä sveitsiläiseen matemaatikkoon Leonhard Euleriin. Euler vahvisti Ehlerin hypoteesin, jonka mukaan ongelmaan ei ollut ratkaisua, ja Eulerin selitys pohjusti uutta matemaattista paradigmaa, jota kutsuttiin sijainnin geometriaksi.
Eulerin uudessa geometrian paradigmassa todettiin, että siltojen sijainnilla ei ollut merkitystä. Sen sijaan ongelmaa voidaan yksinkertaistaa muuttamalla jokainen silta pisteeksi (solmuksi), jonka välisiä yhteyksiä edustavat viivat (reunat). Tämä solmujen ja reunojen käyttökäytäntö tunnetaan nykyään nimellä graafiteoria.
Kunigsbergin sillat -ongelmasta voit lukea lisää täältä.
Alun perin grafiikkateorialla ei ollut juurikaan käyttöä ongelmanratkaisussa, eikä se ollut matemaattikoiden keskuudessa kovinkaan suuressa arvossa. Nykyaikainen laskentateho suurten permutaatioiden käsittelyyn on kuitenkin tehnyt graafiteorian periaatteista käytännöllisempiä. Tässä artikkelissa opetetaan soveltamaan Graafiteorian periaatteita Python-pohjaiseen analyysiin.




>
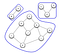
Graafin järjestelmään kuuluvat tietoverkot eivät ole keskenään kytköksissä. Tämä yhteyksien katkeaminen tapahtuu komponenttien muodostuessa. Kuten alla olevassa kuvaajassa näkyy, komponentti muodostuu vain silloin, kun jokaisella solmulla on polku muihin solmuihin.
Sovellettu graafiteoria Pythonissa
Pythonissa networkx:ää käytetään usein sovellettuun graafiteoriaan, jota kutsutaan myös verkkoanalyysiksi . Paketissa on hyödyllisiä toimintoja, joiden avulla voidaan nopeasti tehdä yhteenveto graafin ominaisuuksista. Voit tarkastella alla olevia vaiheita ja seurata mukana, kun luomme graafin ja ymmärrämme sen koostumuksen.
Aluksi alla oleva koodi luo graafin tyhjän objektin P. Seuraavissa vaiheissa lisätään solmuja ja kuvataan särmiä.
Argumentit, kuten <object>.nodes() tai <object>.edges(), ovat nopeita tapoja tarkastella graafijärjestelmän kaikkia solmuja ja särmiä.
print(P.nodes())print(P.edges())
Viimeiseksi nx.draw käytetään verkon visualisointiin.
%matplotlib inline
import matplotlib.pyplot as plt
nx.draw(P, with_labels = True)
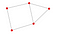
Harjoitukset 1:
Nyt kun graafien peruskäsitteitä on käsitelty, seuraavat harjoitukset ovat hyvä menetelmä harjoitteluun:
- Miten monta solmua yllä olevassa graafissa on?
- Miten monta särmää yllä olevassa graafissa on?
- Mikä on E:n ja C:n geodeesi?
- Onko graafissa enemmän kuin yksi komponentti?
Todellisen datan käyttäminen
Alhaalla olevassa harjoituksessa käytetään tietoja lennoista Unites Statesin sisällä vuonna 2015. Tietoaineisto sisältää lähtö- ja kohdelentoasemat sekä lentoa kuvaavat attribuutit, mukaan lukien lentoaika ja myöhästymiset (säähän, turvallisuuteen tai lentoyhtiöön liittyvät).
Koska aineisto on laaja, harjoituksessa keskitytään Los Angelesin alueen lentoasemilta (Los Angeles (LAX), Burbank (BUR), Orange County (SNA) ja San Bernardino County (ONT)) lähteviin lentoihin. Lisäksi keskitytään tarkastelemaan lentoja, jotka muistuttavat Deloitten matka-aikatauluani – lennän sunnuntaisin ja palaan torstaisin.
Koska meillä on jo lähtö- ja määräpaikkatiedot, ****kentät ORIGIN_AIRPORT ja DESTINATION_AIRPORT toimivat solmujen ja särmien lähdekenttinä – solmuja ja särmiä ei tarvitse luoda, kuten ensimmäisessä harjoituksessa tehtiin. Kun solmut on määritelty, <object>.edges() tarjoaa kaikki niiden väliset pareittaiset suhteet. Lopuksi nx.draw auttaa tuottamaan graafin reunoille.

FG.edges()

nx.draw(FG, with_labels = True)

Yllä olevassa tulosteessa, solmut on merkitty lentoasemakoodeilla. Kaikki särmät johtavat jollekin neljästä Los Angelesin alueen lentoasemasta, koska vain nämä neljä valittiin tähän harjoitukseen. Los Angelesin kansainvälinen lentoasema (LAX) on suurin näistä neljästä lentoasemasta, ja kuvaajasta käy selvästi ilmi, että moniin kaupunkeihin pääsee vain LAX:ltä eikä muilta pienemmiltä lentoasemilta. Tämä osoittaa LAX:n kytkeytyneisyyden eli astekeskeisyyden. Networkx:ssä nx.algorithms.degree_centrality(<object>) ****käytetään kunkin solmun keskeisyyden löytämiseksi graafijärjestelmässä.
# Calculating the centrality of each of the airports
nx.algorithms.degree_centrality(FG)
Voidaan mennä yksityiskohtaisemmaksi ja käyttää lyhyttä ’for-silmukkaa’ tuottamaan kahden kiinnostavan alueen välisiä reunoja. Esimerkiksi seuraavan koodin avulla etsitään kaikki mahdolliset lennot San Bernardinon piirikunnasta (ONT) Newarkiin (EWR) joko sunnuntaina tai torstaina.
San Bernardinon piirikunnan ja Newarkin välisten useiden lentovaihtoehtojen joukosta voidaan nx.dijkstra_path:n avulla etsiä euklidinen polku (tai lyhin polku).
#Finding the dijkstra path
djk_path = nx.dijkstra_path(FG, source='ONT', target='EWR')
djk_path
Harjoituksia 2:
- Tuota seuraava graafi käyttämällä
nx.draw(). Huomaa: verkkosi ei välttämättä näytä täsmälleen samalta, mutta polkujen, särmien ja solmujen pitäisi vastata alla olevaa verkkoa. - Tulosta kaikki särmät.
- Mikä on lyhin polku L:stä F:ään?
