Im letzten Tutorial haben wir kurz über Filter gesprochen. In diesem Tutorium werden wir sie ausführlich besprechen. Bevor wir darüber sprechen, wollen wir zuerst über Masken sprechen. Das Konzept der Maske wurde in unserem Tutorium über Faltung und Masken besprochen.

Weichzeichnermasken vs. abgeleitete Masken

Wir werden einen Vergleich zwischen Weichzeichnermasken und abgeleiteten Masken durchführen.

Weichzeichnermasken

Eine Weichzeichnermaske hat die folgenden Eigenschaften.

• Alle Werte in Unschärfemasken sind positiv
• Die Summe aller Werte ist gleich 1
• Der Kanteninhalt wird durch eine Unschärfemaske reduziert
• Je größer die Maske wird, desto mehr Glättungseffekt tritt ein

Derivative Masken

Eine derivative Maske hat folgende Eigenschaften.

• Eine derivative Maske hat sowohl positive als auch negative Werte
• Die Summe aller Werte in einer derivativen Maske ist gleich Null
• Der Kanteninhalt wird durch eine derivative Maske erhöht
• Mit zunehmender Größe der Maske wird der Kanteninhalt erhöht

Beziehung zwischen Unschärfemaske und derivativer Maske mit Hochpassfiltern und Tiefpassfiltern.

Die Beziehung zwischen Unschärfemaske und abgeleiteter Maske mit Hochpassfilter und Tiefpassfilter kann einfach wie folgt definiert werden.

• Unschärfemasken werden auch als Tiefpassfilter bezeichnet
• Abgeleitete Masken werden auch als Hochpassfilter bezeichnet

Hochpass-Frequenzkomponenten und Tiefpass-Frequenzkomponenten

Die Hochpass-Frequenzkomponenten bezeichnen Kanten, während die Tiefpass-Frequenzkomponenten glatte Bereiche bezeichnen.

Idealer Tiefpass und idealer Hochpass

Dies ist das übliche Beispiel für einen Tiefpassfilter.

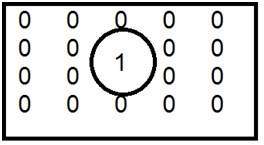
Wenn man die Eins nach innen und die Null nach außen setzt, erhält man ein unscharfes Bild. Wenn wir nun die Größe der 1 erhöhen, würde die Unschärfe zunehmen und der Kanteninhalt reduziert werden.

Dies ist ein allgemeines Beispiel für einen Hochpassfilter.

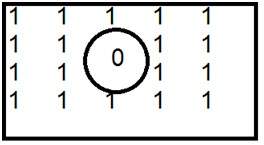
Wenn die 0 innen platziert wird, erhalten wir Kanten, was uns ein skizzenhaftes Bild liefert. Ein idealer Tiefpassfilter im Frequenzbereich ist unten angegeben.

Der ideale Tiefpassfilter kann grafisch dargestellt werden als

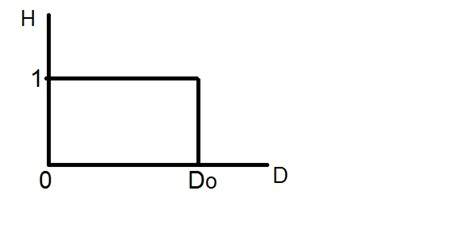
Wenden wir nun diesen Filter auf ein tatsächliches Bild an und sehen wir, was wir erhalten.

Beispielbild

Bild im Frequenzbereich

Anwendung des Filters auf dieses Bild

Ergebnisbild

Auf die gleiche Weise kann ein idealer Hochpassfilter auf ein Bild angewendet werden. Aber die Ergebnisse wären natürlich unterschiedlich, da der Tiefpass den kantigen Inhalt reduziert und der Hochpass ihn erhöht.

Gauß’scher Tiefpass und Gauß’scher Hochpass

Gauß’scher Tiefpass und Gauß’scher Hochpass minimieren das Problem, das bei idealen Tiefpass- und Hochpassfiltern auftritt.

Dieses Problem ist als Ringing-Effekt bekannt. Der Grund dafür ist, dass an einigen Punkten der Übergang zwischen einer Farbe und der anderen nicht genau definiert werden kann, wodurch der Ringing-Effekt an diesem Punkt auftritt.

Schauen Sie sich dieses Diagramm an.

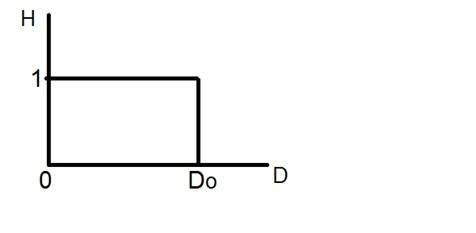
Dies ist die Darstellung des idealen Tiefpassfilters. Am genauen Punkt von Do kann man nicht sagen, ob der Wert 0 oder 1 ist. Aufgrund dessen erscheint der Klingel-Effekt an diesem Punkt.

Um also den Effekt zu reduzieren, der bei idealen Tiefpass- und Hochpassfiltern auftritt, wird der folgende Gaußsche Tiefpassfilter und Gaußsche Hochpassfilter eingeführt.

Gaußscher Tiefpassfilter

Das Konzept des Filterns und des Tiefpasses bleibt dasselbe, aber nur der Übergang wird anders und wird glatter.

Der Gaußsche Tiefpassfilter kann wie folgt dargestellt werden

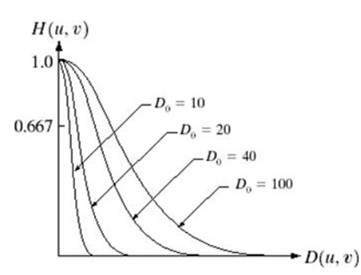
Beachte den sanften Kurvenübergang, durch den an jedem Punkt der Wert von Do genau definiert werden kann.

Gaußscher Hochpassfilter

Das Konzept des gaußschen Hochpassfilters ist dasselbe wie das des idealen Hochpassfilters, aber auch hier ist der Übergang glatter als beim idealen Filter.