I den sidste tutorial diskuterede vi kort om filtre. I denne tutorial vil vi diskutere dem grundigt. Inden vi diskuterer om, skal vi først tale om masker. Begrebet maske er blevet diskuteret i vores tutorial om konvolution og masker.

Blurring masks vs derivative masks

Vi vil foretage en sammenligning mellem blurring masks og derivative masks.

Blurring masks

En blurring maske har følgende egenskaber.

• Alle værdier i sløringsmasker er positive
• Summen af alle værdierne er lig med 1
• Kantindholdet reduceres ved at bruge en sløringsmaske
• Da maskens størrelse vokser, vil der ske en større udglatningseffekt

Derivative masker

En derivativ maske har følgende egenskaber.

• En afledt maske har positive og såvel som negative værdier
• Summen af alle værdierne i en afledt maske er lig med nul
• Kantindholdet øges ved en afledt maske
• Da størrelsen af masken vokser , øges mere kantindhold

Sammenhæng mellem sløringsmaske og afledt maske med højpasfiltre og lavpasfiltre.

Forholdet mellem sløringsmaske og afledt maske med et højpasfilter og et lavpasfilter kan defineres simpelt som:

• Sløringsmasker kaldes også for lavpasfilter
• Derivatmasker kaldes også for højpasfilter

Højpasfrekvenskomponenter og lavpasfrekvenskomponenter

Højpasfrekvenskomponenterne betegner kanter, mens lavpasfrekvenskomponenterne betegner glatte områder.

Ideal low pass og ideal high pass-filter

Dette er det almindelige eksempel på low pass-filter.

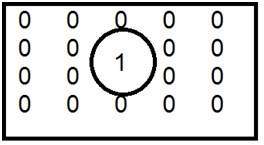
Når et er placeret indenfor, og nul er placeret udenfor , får vi et sløret billede. Når vi nu øger størrelsen af 1, vil sløringen øges, og kantindholdet vil blive reduceret.

Dette er et almindeligt eksempel på højpasfilter.

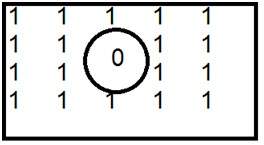
Når 0 placeres indenfor, får vi kanter, hvilket giver os et skitseret billede. Et ideelt lavpasfilter i frekvensdomænet er givet nedenfor.

Det ideelle lavpasfilter kan grafisk fremstilles som

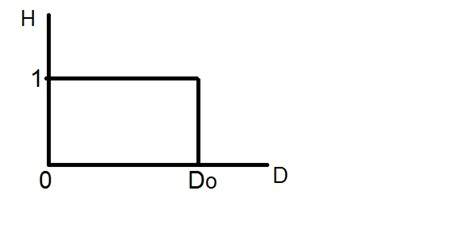
Nu skal vi anvende dette filter på et faktisk billede, og lad os se, hvad vi har fået.

Stikprøvebillede

Billede i frekvensdomæne

Anvendelse af filter over dette billede

Resultatbillede

Med samme fremgangsmåde kan et ideelt high pass-filter anvendes på et billede. Men resultaterne vil naturligvis være forskellige, da lavpas reducerer det kantede indhold, og højpas øger det.

Gaussiansk lavpas og Gaussisk højpasfilter

Gaussiansk lavpas og Gaussisk højpasfilter minimerer det problem, der opstår i ideelle lavpas- og højpasfiltre.

Dette problem er kendt som ringing-effekt. Det skyldes, at overgangen mellem den ene farve og den anden farve på nogle punkter ikke kan defineres præcist, og at ringing-effekten opstår på dette punkt.

Se på denne graf.

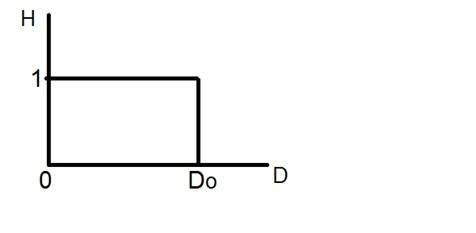
Dette er repræsentationen af det ideelle lavpasfilter. Nu på det nøjagtige punkt af Do kan man ikke sige, at værdien ville være 0 eller 1. På grund af hvilket den ringende effekt vises på det punkt.

Så for at reducere den effekt, der vises er ideelt lavpas og ideelt højpasfilter, indføres følgende Gaussisk lavpasfilter og Gaussisk højpasfilter.

Gaussiansk lavpasfilter

Konceptet med filtrering og lavpas forbliver det samme, men kun overgangen bliver anderledes og bliver mere jævn.

Det Gaussiske lavpasfilter kan repræsenteres som

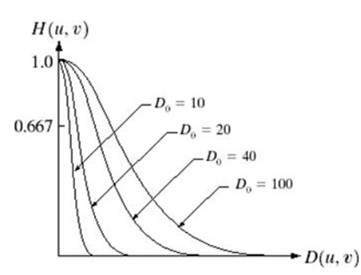
Bemærk den glatte kurveovergang, på grund af hvilken i hvert punkt kan værdien af Do, defineres nøjagtigt.

Gaussiansk højpasfilter

Gaussiansk højpasfilter har samme koncept som det ideelle højpasfilter, men igen er overgangen mere jævn i forhold til det ideelle.