Grafteori – en introduktion til Python

november 7, 2021
| Ingen kommentarer
Sofiyan Sheikh

Follow

15. jan, 2019 – 6 min read

Et voksende område af interesse for forskere, der udforsker betydning, magt eller indflydelse blandt enheder, kaldes grafteori. Grafteoriens rødder begyndte i 1736, da matematikeren Carl Ehler introducerede Leonhard Euler til broerne i Konigsberg-problemet.

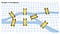
Broerne i Konigsberg-problemet er baseret på den tidligere tyske by Konigsberg, der ligger på begge sider af floden Pregel. I midten var der to store øer, som var forbundet med hinanden og med flodbredderne ved hjælp af syv broer. Carl Ehler blev besat af at finde en rute, hvor man kunne gå gennem hver af de syv broer uden at gå over nogen af dem mere end én gang. Ehler henvendte sig til Leonhard Euler, en schweizisk matematiker. Euler bekræftede Ehlers hypotese om, at problemet ikke havde en løsning, og Eulers forklaring dannede grundlag for et nyt matematisk paradigme kaldet Geometry of Position.

Eulers nye geometriparadigme fastslog, at placeringen af broerne var ligegyldig. Problemet kan i stedet forenkles ved at gøre hver bro til et punkt (knude) med linjer (kanter) til at repræsentere forbindelserne mellem dem. Denne praksis med at bruge knuder og kanter er nu kendt som grafteori.

Du kan læse mere om broerne i Konigsberg-problemet her.

I første omgang tjente grafteorien ikke meget til problemløsning og blev ikke højt anset af matematikere. Moderne computerkraft til at behandle store permutationer har imidlertid gjort Graph Theory’s principper mere praktiske. I denne artikel lærer du at anvende Graph Theory-principperne på Python-baserede analyser.

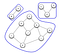
Det er ikke alle netværk i et Graph-system, der er indbyrdes forbundne. Denne afbrydelse af forbindelsen sker, når der dannes komponenter. Som vist i grafen nedenfor dannes en komponent kun, når hver knude har en sti til andre knuder.

Anvendt grafteori i Python

I Python bruges networkx ofte til anvendt grafteori også kendt som netværksanalyse . Pakken har nyttige funktioner til hurtigt at opsummere egenskaberne ved en graf. Du kan gennemgå nedenstående trin og følge med, mens vi opretter en graf og forstår dens opbygning.

Først opretter nedenstående kode et tomt grafobjekt P. De næste trin tilføjer knuder og beskriver kanterne.

Argumenter som <object>.nodes() eller <object>.edges() er hurtige måder at få vist alle knuder og kanter i grafsystemet.

print(P.nodes())print(P.edges())

Sluttelig bruges nx.draw til at visualisere netværket.

%matplotlib inline
import matplotlib.pyplot as plt
nx.draw(P, with_labels = True)

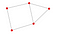
Øvelser 1:

Nu da de grundlæggende begreber om grafer er gennemgået, er følgende øvelser en god metode til at øve sig:

  • Hvor mange knuder er der i ovenstående graf?
  • Hvor mange kanter er der i ovenstående graf?
  • Hvad er geodætisk for E og C?
  • Er der mere end 1 komponent i grafen?

Anvendelse af virkelige data

I nedenstående øvelse anvendes data for flyvninger inden for Unites States i 2015. Datasættet omfatter oprindelses- og destinationslufthavne ud over attributter, der beskriver flyvningen, herunder flyvetid og forsinkelser (vejr-, sikkerheds- eller flyselskabsrelaterede).

Da datasættet er stort, vil øvelsen koncentrere sig om flyvninger med udgangspunkt i lufthavne i Los Angeles-området (Los Angeles (LAX), Burbank (BUR), Orange County (SNA) og San Bernardino County (ONT)). Desuden vil der blive fokuseret på at gennemgå flyvninger, der ligner min Deloitte-rejseplan – flyvning ud om søndagen og hjem om torsdagen.

Da vi allerede har oprindelses- og destinationsdata, vil ****fields ORIGIN_AIRPORT og DESTINATION_AIRPORT tjene som kildefelter for knuder og kanter – der er ikke behov for at oprette knuder eller kanter, som vi gjorde i den første øvelse. Når knuder er defineret, vil <object>.edges() levere alle parvise relationer mellem dem. Endelig vil nx.draw hjælpe med at fremstille en graf til kanterne.

FG.edges()

nx.draw(FG, with_labels = True)

I ovenstående output, er knuderne mærket med lufthavnskoder. Alle kanter fører til en af de fire lufthavne i Los Angeles-området, fordi disse fire var de eneste, der blev udvalgt til denne øvelse. Los Angeles International (LAX) er den største lufthavn blandt de fire, og det fremgår tydeligt af grafen, at mange byer kun er tilgængelige fra LAX og ikke fra andre mindre lufthavne. Dette viser LAX’s forbundethed eller grad af centralitet. I networkx bruges nx.algorithms.degree_centrality(<object>) **** til at finde centralitet for hver enkelt knude i grafsystemet.

# Calculating the centrality of each of the airports
nx.algorithms.degree_centrality(FG)

Vi kan gå mere granulært til værks og bruge en kort “for loop” til at producere kanter mellem to områder af interesse. F.eks. bruges følgende kode til at finde alle mulige flyvninger fra San Bernardino County (ONT) til Newark (EWR) enten søndag eller torsdag.

Mellem de mange flyvemuligheder mellem San Bernardino County og Newark kan nx.dijkstra_path bruges til at finde den euklidiske vej (eller den korteste vej).

#Finding the dijkstra path
djk_path = nx.dijkstra_path(FG, source='ONT', target='EWR')
djk_path

Øvelser 2:

  • Producer følgende graf ved hjælp af nx.draw(). Bemærk: Dit netværk ser måske ikke helt ens ud, men stierne, kanterne og knuderne skal stemme overens med nedenstående netværk.
  • Udskriv alle kanterne.
  • Hvad er den korteste vej fra L til F?

Articles