V minulém tutoriálu jsme si stručně řekli něco o filtrech. V tomto tutoriálu o nich budeme hovořit důkladně. Než o nich začneme diskutovat, řekneme si nejprve něco o maskách. Pojem masky jsme probrali v našem tutoriálu o konvoluci a maskách.

Rozmazávací masky vs. derivační masky

Provedeme srovnání mezi rozmazávacími a derivačními maskami.

Rozmazávací masky

Rozmazávací maska má následující vlastnosti.

• Všechny hodnoty v rozostřovacích maskách jsou kladné
• Součet všech hodnot je roven 1
• Použitím rozostřovací masky se sníží obsah hran
• S rostoucí velikostí masky dojde k většímu efektu vyhlazení

Derivační masky

Derivační maska má následující vlastnosti.

• Derivační maska má kladné i záporné hodnoty
• Součet všech hodnot v derivační masce je roven nule
• Obsah hran se derivační maskou zvětšuje
• S rostoucí velikostí masky , se zvětšuje větší obsah hran

Souvislost mezi rozostřovací maskou a derivační maskou s hornopropustnými filtry a dolnopropustnými filtry.

Vztah mezi rozostřovací maskou a derivační maskou s hornopropustným filtrem a dolnopropustným filtrem lze jednoduše definovat takto:

• Rozostřovací masky se nazývají také jako dolnopropustný filtr
• Derivační masky se nazývají také jako hornopropustný filtr

Vysokofrekvenční složky a nízkofrekvenční složky

Vysokofrekvenční složky označují hrany, zatímco nízkofrekvenční složky označují hladké oblasti.

Ideální dolní propust a ideální horní propust filtru

Toto je běžný příklad dolní propusti filtru.

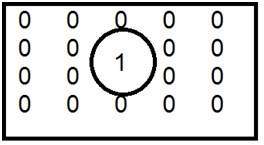
Když je jednička umístěna uvnitř a nula vně , dostali jsme rozmazaný obraz. Když nyní zvětšíme velikost jedničky, rozmazání se zvýší a obsah hran se sníží.

Jedná se o běžný příklad hornopropustného filtru.

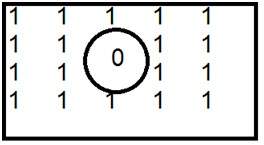
Když je nula umístěna uvnitř, dostaneme hrany, čímž získáme načrtnutý obraz. Ideální dolnopropustný filtr ve frekvenční oblasti je uveden níže.

Ideální dolnopropustný filtr lze graficky znázornit jako

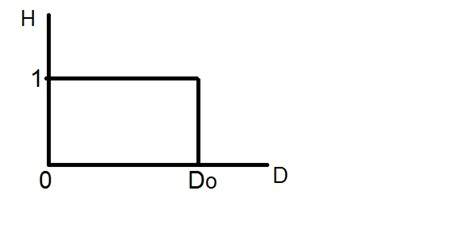
Nyní aplikujme tento filtr na skutečný obraz a podívejme se, co jsme získali.

Vzorový obrázek

Obrázek ve frekvenční oblasti

Při aplikaci filtru na tento obrázek

Výsledný obrázek

Stejným způsobem lze na obrázek aplikovat ideální filtr vysoké propustnosti. Je však zřejmé, že výsledky by se lišily, protože dolní propust snižuje okrajový obsah a horní propust jej zvyšuje.

Gausův dolní a Gaussův horní filtr

Gausův dolní a Gaussův horní filtr minimalizují problém, který se vyskytuje u ideálního dolního a horního filtru.

Tento problém je znám jako efekt zvonění. Je to z toho důvodu, že v některých bodech nelze přesně definovat přechod mezi jednou barvou a druhou, kvůli čemuž se v tomto bodě objevuje zvonivý efekt.

Podívejte se na tento graf.

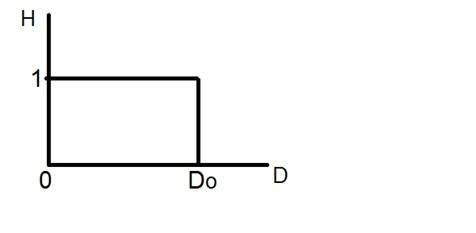
Toto je zobrazení ideálního dolnopropustného filtru. Nyní v přesném bodě Do nelze říci, že by hodnota byla 0 nebo 1. Kvůli čemuž se v tomto bodě objevuje efekt zvonění.

Pro snížení efektu, který se objevuje, je tedy ideální dolní propust a ideální horní propust zaveden následující Gaussův filtr dolní propust a Gaussův filtr horní propust.

Gaussův filtr dolní propust

Koncept filtrování a dolní propust zůstává stejný, ale pouze přechod se stává jiným a stává se hladším.

Gausův dolnopropustný filtr lze znázornit jako

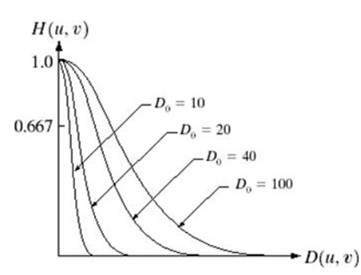
Všimněte si hladkého přechodu křivky, díky němuž lze v každém bodě přesně definovat hodnotu Do.

Gausův filtr horní propust

Gausův filtr horní propust má stejnou koncepci jako ideální filtr horní propust, ale opět je přechod oproti ideálnímu hladší.

.