Menos…
Un triple pitagórico es un triple de enteros positivos 
, 
, y 
tal que existe un triángulo rectángulo con catetos 
e hipotenusa 
. Por el teorema de Pitágoras, esto equivale a encontrar enteros positivos 
, 
, y 
que satisfagan
 |
(1)
|
El triple pitagórico más pequeño y conocido es 
. El triángulo rectángulo que tiene estas longitudes de lado se llama a veces triángulo 3, 4, 5.
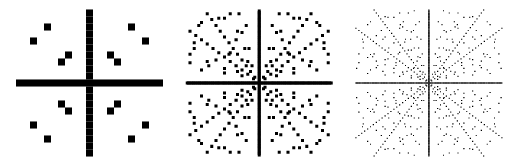
Las gráficas de puntos en el plano 
tales que 
es un triple pitagórico se muestran arriba para límites sucesivamente mayores. Estos gráficos incluyen valores negativos de 
y 
, y por lo tanto son simétricos con respecto a los ejes x y y.
De manera similar, los gráficos de puntos en el plano 
tales que 
es un triple pitagórico se muestran arriba para límites sucesivamente mayores.
Es habitual considerar sólo los triples pitagóricos primitivos (también llamados «reducidos») en los que 
y 
son relativamente primos, ya que se pueden generar trivialmente otras soluciones a partir de los primitivos. Los triples primitivos se ilustran arriba, y se puede ver inmediatamente que las líneas radiales correspondientes a los triples imprimibles en el gráfico original están ausentes en esta figura. Para las soluciones primitivas, una de 
o 
debe ser par, y la otra impar (Shanks 1993, p. 141), siendo 
siempre impar.
Además, un lado de cada triple pitagórico es divisible por 3, otro por 4 y otro por 5. Un lado puede tener dos de estos divisores, como en (8, 15, 17), (7, 24, 25) y (20, 21, 29), o incluso los tres, como en (11, 60, 61).
Dado un triple primitivo 
, se obtienen tres nuevos triples primitivos de
 |
 |
 |
(2)
|
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
donde
 |
 |
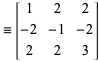(5)
|
 |
 |
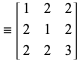(6)
|
 |
 |
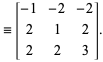(7)
|
Hall (1970) y Roberts (1977) demuestran que 
es un triple pitagórico primitivo si
 |
(8)
|
donde 
es un producto finito de las matrices 
, 
, 
. Por lo tanto, se deduce que cada triple pitagórico primitivo debe ser un miembro de la matriz infinita
 |
(9)
|
Pitágoras y los babilonios dieron una fórmula para generar triples (no necesariamente primitivos) como
 |
(10)
|
para 
, lo que genera un conjunto de triples distintos que no contiene ni todos los primitivos ni todos los imprimibles (y donde en el caso especial 
, 
).
Los primeros griegos dieron
 |
(11)
|
donde 
y 
son relativamente primos y de paridad opuesta (Shanks 1993, p. 141), lo que genera un conjunto de triples distintos que contiene precisamente los triples primos (después de ordenar adecuadamente 
y 
).
Sea 
un número de Fibonacci. Entonces
 |
(12)
|
genera distintos triples pitagóricos (Dujella 1995), aunque no de forma exhaustiva ni para los primitivos ni para los imprimibles. De forma más general, partiendo de los enteros positivos 
, 
, y construyendo la secuencia tipo Fibonacci 
con los términos 
, 
, 
, 
, 
, … genera triples pitagóricos distintos
 |
(13)
|
(Horadam 1961), donde
 |
(24)
|
(Beiler 1966, p. 116). Nótese que 
si 
es primo o dos veces primo. Los primeros números para 
, 2, … son 0, 0, 1, 1, 1, 1, 1, 2, 2, 1, 1, 4, 1, … (OEIS A046079).
Para hallar el número de formas 
en que un número 
puede ser la hipotenusa de un triángulo rectángulo primitivo, se escribe su factorización como
 |
(25)
|
donde los 
s son de la forma 
y los 
s son de la forma 
. El número de posibles triángulos rectos primitivos es entonces
 |
(26)
|
Por ejemplo, 
ya que
 |
 |
 |
(27)
|
 |
 |
 |
(28)
|
Los valores de 
para 
, 2, … son 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, … (OEIS A024362). Los primeros primos de la forma 
son 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, … (OEIS A002144), por lo que las menores longitudes de los lados que son las hipotenusas de 1, 2, 4, 8, 16, … triángulos rectángulos primitivos son 5, 65, 1105, 32045, 1185665, 48612265, … (OEIS A006278).
El número de posibles triángulos rectángulos primitivos o no primitivos que tienen 
como hipotenusa es
 |
 |
 |
(29)
|
 |
 |
 |
(30)
|
(corrigiendo la errata de Beiler 1966, p. 117, que afirma que esta fórmula sólo da el número de soluciones no primitivas), donde 
es la función de suma de cuadrados. Por ejemplo, hay cuatro triángulos enteros distintos con hipotenusa 65, ya que
 |
(31)
|
Los primeros números para 
, 2, … son 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, … (OEIS A046080). Los hipotenus más pequeños que tienen 
triples distintos son 1, 5, 25, 125, 65, 3125, … (OEIS A006339). La siguiente tabla da los hipotenus para los que existen exactamente 
triángulos enteros rectos distintos para 
, 1, …, 5.
 |
OEIS | hipotenus para los que existen  triángulos enteros distintos |
| 0 | A004144 | 1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, … |
| 1 | A084645 | 5, 10, 13, 15, 17, 20, 26, 29, 30, 34, 35, … |
| 2 | A084646 | 25, 50, 75, 100, 150, 169, 175, 200, 225, … |
| 3 | A084647 | 125, 250, 375, 500, 750, 875, 1000, 1125, 1375, … |
| 4 | A084648 | 65, 85, 130, 145, 170, 185, 195, 205, 221, 255, … |
| 5 | A084649 | 3125, 6250, 9375, 12500, 18750, 21875, 25000, … |
Por tanto, el número total de formas en que 
puede ser un cateto o una hipotenusa de un triángulo rectángulo viene dado por
 |
(32)
|
Los valores de 
, 2, … son 0, 0, 1, 1, 2, 1, 1, 2, 2, 2, 1, 4, 2, 1, 5, 3, … (OEIS A046081). Los números más pequeños 
que pueden ser los lados de 
triángulos rectángulos generales para 
, 2, … son 3, 5, 16, 12, 15, 125, 24, 40, … (OEIS A006593; Beiler 1966, p. 114).
Hay 50 triples pitagóricos con hipotenusa menor que 100, los primeros de los cuales, ordenados por 
creciente, son (3, 4, 5), (6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083, A046084 y A009000).
De ellos, sólo 16 son tripletes primitivos con hipotenusa menor que 100: (3, 4,5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65), (16, 63, 65), (48, 55, 73), (36, 77, 85), (13, 84, 85), (39, 80, 89) y (65, 72, 97) (OEIS A046086, A046087 y A020882).
Dejemos que el número de triples con hipotenusa 
se denote 
, el número de triples con hipotenusa 
se denote 
, y el número de triples primitivos menores que 
se denote 
. A continuación, la siguiente tabla resume los valores de las potencias de 10.
 |
OEIS |  ,  , … |
 |
A101929 | 1, 50, 878, 12467, … |
 |
A101930 | 2, 52, 881, 12471, … |
 |
A101931 | 1, 16, 158, 1593, … |
Lehmer (1900) demostró que el número de soluciones primitivas con hipotenusa menor que 
satisface
 |
(33)
|
(OEIS A086201).
Los inradios de los primeros triángulos pitagóricos primitivos ordenados de forma creciente 
vienen dados por 1, 2, 3, 3, 6, 5, 4, 10, 5, … (OEIS A014498).
Hay un método general para obtener tripletes de triángulos pitagóricos con áreas iguales. Tomemos los tres conjuntos de generadores como
 |
 |
 |
(34)
|
 |
 |
 |
(35)
|
 |
 |
 |
(36)
|
 |
 |
 |
(37)
|
 |
 |
 |
(38)
|
 |
 |
 |
(39)
|
Entonces el triángulo rectángulo generado por cada triple (
) tiene área común
 |
(40)
|
(Beiler 1966, pp. 126-127). El único extremo de esta función ocurre en 
. Dado que 
para 
, el área más pequeña compartida por tres triángulos rectángulos no primitivos viene dada por 
, que da como resultado un área de 840 y corresponde a los tripletes (24, 70, 74), (40, 42, 58) y (15, 112, 113) (Beiler 1966, p. 126).
Los triángulos rectos cuyas áreas consisten en un solo dígito incluyen 
(área de 6) y 
(área de 666666; Wells 1986, p. 89).
En 1643, Fermat desafió a Mersenne a encontrar un triplete pitagórico cuya hipotenusa y suma de los catetos fueran cuadrados. Fermat encontró la solución más pequeña de este tipo:
 |
 |
 |
(41)
|
 |
 |
 |
(42)
|
 |
 |
 |
(43)
|
con
 |
 |
 |
(44)
|
 |
 |
 |
(45)
|
Un problema relacionado es determinar si un entero especificado 
puede ser el área de un triángulo rectángulo con lados racionales. 1, 2, 3 y 4 no son las áreas de ningún triángulo rectángulo de lados racionales, pero 5 sí lo es (3/2, 20/3, 41/6), al igual que 6 (3, 4, 5). La solución del problema implica la curva elíptica
 |
(46)
|
Una solución (
, 
, 
) existe si (46) tiene una solución racional, en cuyo caso
 |
 |
 |
(47)
|
 |
 |
 |
(48)
|
(Koblitz 1993). No se conoce un método general para determinar si existe una solución para 
arbitrarios, pero una técnica ideada por J. Tunnell en 1983 permite descartar ciertos valores (Cipra 1996).