Less…
En pythagoreisk trippel är en trippel av positiva heltal 
, 
och 
så att en rätvinklig triangel existerar med benen 
och hypotenusen 
. Enligt Pythagoras sats är detta likvärdigt med att hitta positiva heltal 
, 
och 
som uppfyller
 |
(1)
|
Den minsta och mest kända pythagoriska trippeln är 
. Den rätvinkliga triangel som har dessa sidlängder kallas ibland för 3, 4, 5-triangeln.
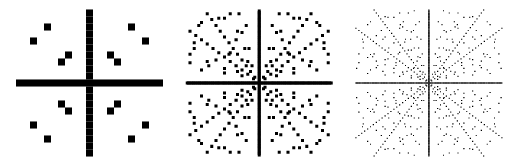
Plottar av punkter i 
-planet så att 
är en pythagoreisk triangel visas ovan för successivt större gränser. Dessa diagram inkluderar negativa värden av 
och 
och är därför symmetriska kring både x- och y-axeln.
På samma sätt visas ovan diagram för punkter i 
-planet så att 
är en pythagorisk trippel för successivt större gränser.
Det är vanligt att endast beakta primitiva pythagoreiska triplar (även kallade ”reducerade ”triplar) där 
och 
är relativt primära, eftersom andra lösningar kan genereras trivialt från de primitiva. De primitiva tripplarna illustreras ovan, och man kan omedelbart se att de radiella linjerna som motsvarar imprimitiska tripplar i den ursprungliga plotten saknas i den här figuren. För primitiva lösningar måste en av 
eller 
vara jämn och den andra udda (Shanks 1993, s. 141), med 
alltid udda.
Den ena sidan av varje pythagorisk trippel är dessutom delbar med 3, en annan med 4 och en annan med 5. En sida kan ha två av dessa delare, som i (8, 15, 17), (7, 24, 25) och (20, 21, 29), eller till och med alla tre, som i (11, 60, 61).
Givet en primitiv trippel 
erhålls tre nya primitiva triplar från
 |
 |
 |
(2)
|
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
hos
 |
 |
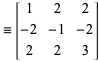(5)
|
 |
 |
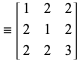(6)
|
 |
 |
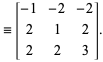(7)
|
Hall (1970) och Roberts (1977) bevisar att 
är en primitiv pythagoreisk trippel om
 |
(8)
|
där 
är en ändlig produkt av matriserna 
, 
, 
. Av detta följer att varje primitiv pythagorisk trippel måste ingå i den oändliga matrisen
 |
(9)
|
Pythagoras och babylonierna gav en formel för att generera (inte nödvändigtvis primitiva) triplar som
 |
(10)
|
för 
, som genererar en uppsättning distinkta triplar som varken innehåller alla primitiva eller alla imprimitiva triplar (och där i specialfallet 
, 
).
De tidiga grekerna gav
 |
(11)
|
där 
och 
är relativt primtal och av motsatt paritet (Shanks 1993, p. 141), vilket genererar en uppsättning distinkta triplar som innehåller just de primitiva triplarna (efter lämplig sortering av 
och 
).
Låt 
vara ett Fibonacci-tal. Då
 |
(12)
|
genererar distinkta pythagoriska triplar (Dujella 1995), dock inte uttömmande för vare sig primitiva eller imprimitiva triplar. Mer allmänt kan man börja med positiva heltal 
, 
och konstruera den Fibonacci-liknande sekvensen 
med termerna 
, 
, 
, 
, 
, … genererar distinkta pythagoreiska triplar
 |
(13)
|
(Horadam 1961), där
 |
(24)
|
(Beiler 1966, s. 116). Observera att 
om 
är primtal eller två gånger primtal. De första talen för 
, 2, … är 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1, 1, 4, 1, … (OEIS A046079).
För att hitta antalet sätt 
på vilka ett tal 
kan vara hypotenusan i en primitiv rätvinklig triangel, skriv dess faktorisering som
 |
(25)
|
där 
s är av formen 
och 
s är av formen 
. Antalet möjliga primitiva rätvinkliga trianglar är då
 |
(26)
|
Till exempel, 
eftersom
 |
 |
 |
(27)
|
 |
 |
 |
(28)
|
Värdena för 
för 
, 2, … är 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, … (OEIS A024362). De första primtalen av formen 
är 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, … (OEIS A002144), så de minsta sidlängderna som är hypotenus i 1, 2, 4, 8, 16, … primitiva rätvinkliga trianglar är 5, 65, 1105, 32045, 1185665, 48612265, … (OEIS A006278).
Antalet möjliga primitiva eller icke-primitiva rätvinkliga trianglar med 
som hypotenusa är
 |
 |
 |
(29)
|
 |
 |
 |
(30)
|
(rättelse av skrivfel i Beiler 1966, p. 117, där det står att denna formel endast ger antalet icke-primitiva lösningar), där 
är summan av kvadraternas funktion. Det finns till exempel fyra distinkta heltalstrianglar med hypotenusa 65, eftersom
 |
(31)
|
De första siffrorna för 
, 2, … är 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, … (OEIS A046080). De minsta hypotenusarna med 
distinkta triplar är 1, 5, 25, 125, 65, 3125, … (OEIS A006339). Följande tabell visar de hypotenuser för vilka det finns exakt 
distinkta högra heltalstrianglar för 
, 1, …, 5.
 |
OEIS | hypotenuser för vilka det finns  distinkta heltals trianglar |
| 0 | A004144 | 1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, … |
| 1 | A084645 | 5, 10, 13, 15, 17, 20, 26, 29, 30, 34, 35, … |
| 2 | A084646 | 25, 50, 75, 100, 150, 169, 175, 200, 225, … |
| 3 | A084647 | 125, 250, 375, 500, 750, 875, 1000, 1125, 1375, … |
| 4 | A084648 | 65, 85, 130, 145, 170, 185, 195, 205, 221, 255, … |
| 5 | A084649 | 3125, 6250, 9375, 12500, 18750, 21875, 25000, … |
Det totala antalet sätt på vilka 
kan vara antingen ett ben eller en hypotenus i en rätvinklig triangel ges av
 |
(32)
|
Värdena för 
, 2, … är 0, 0, 0, 1, 1, 1, 2, 2, 1, 1, 1, 2, 2, 2, 2, 1, 4, 2, 1, 5, 3, … (OEIS A046081). De minsta talen 
som kan vara sidorna till 
allmänna rätvinkliga trianglar för 
, 2, … är 3, 5, 16, 12, 15, 125, 24, 40, … (OEIS A006593; Beiler 1966, s. 114).
Det finns 50 pythagoriska triplar med hypotenusor som är mindre än 100. De första triplarna, sorterade efter ökande 
, är (3, 4, 5), (6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083, A046084 och A009000).
Av dessa är endast 16 primitiva tripletter med hypotenusa mindre än 100: (3, 4,5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65), (16, 63, 65), (48, 55, 73), (36, 77, 85), (13, 84, 85), (39, 80, 89) och (65, 72, 97) (OEIS A046086, A046087 och A020882).
Låt antalet triplar med hypotenusan 
betecknas 
, antalet triplar med hypotenusan 
betecknas 
, och antalet primitiva triplar mindre än 
betecknas 
. Följande tabell sammanfattar sedan värdena för potenser av 10:
 |
OEIS |  ,  , … |
 |
A101929 | 1, 50, 878, 12467, … |
 |
A101930 | 2, 52, 881, 12471, ….. |
 |
A101931 | 1, 16, 158, 1593, … |
Lehmer (1900) bevisade att antalet primitiva lösningar med hypotenusa mindre än 
uppfyller
 |
(33)
|
(OEIS A086201).
Inradii i de första få primitiva pythagoriska trianglarna, ordnade efter ökande 
, ges av 1, 2, 3, 3, 3, 6, 6, 5, 4, 10, 5, … (OEIS A014498).
Det finns en allmän metod för att få fram tripletter av pythagoriska trianglar med lika stora areor. Ta de tre uppsättningarna generatorer som
 |
 |
 |
(34)
|
 |
 |
 |
(35)
|
 |
 |
 |
(36)
|
 |
 |
 |
(37)
|
 |
 |
 |
(38)
|
 |
 |
 |
(39)
|
Då är den rätvinkliga triangel som genereras av varje trippel (
) har gemensam area
 |
(40)
|
(Beiler 1966, pp. 126-127). Det enda extremumet för denna funktion inträffar vid 
. Eftersom 
för 
, ges den minsta yta som delas av tre icke primitiva rätvinkliga trianglar av 
, vilket resulterar i en yta på 840 och motsvarar tripletterna (24, 70, 74), (40, 42, 58) och (15, 112, 113) (Beiler 1966, s. 126).
Högre trianglar vars area består av en enda siffra är bland annat 
(area på 6) och 
(area på 666666; Wells 1986, s. 89).
År 1643 utmanade Fermat Mersenne att hitta en pythagorisk triplett vars hypotenusa och summan av benen var kvadrater. Fermat hittade den minsta sådana lösningen:
 |
 |
 |
(41)
|
 |
 |
 |
(42)
|
 |
 |
 |
(43)
|
med
 |
 |
 |
(44)
|
 |
 |
 |
(45)
|
Ett besläktat problem är att avgöra om ett angivet heltal 
kan vara arean av en rät triangel med rationella sidor. 1, 2, 3 och 4 är inte arean av någon rätvinklig triangel med rationella sidor, men 5 är (3/2, 20/3, 41/6), liksom 6 (3, 4, 5). Lösningen på problemet involverar den elliptiska kurvan
 |
(46)
|
En lösning (
, 
, 
) finns om (46) har en rationell lösning, i vilket fall
 |
 |
 |
(47)
|
 |
 |
 |
(48)
|
(Koblitz 1993). Det finns ingen känd allmän metod för att avgöra om det finns en lösning för godtyckliga 
, men en teknik som utarbetades av J. Tunnell 1983 gör det möjligt att utesluta vissa värden (Cipra 1996).