Över 90 % av naturligt förekommande och konstgjorda fasta ämnen är kristallina. De flesta fasta ämnen bildas med ett regelbundet arrangemang av sina partiklar eftersom de övergripande attraktiva interaktionerna mellan partiklarna maximeras och den totala intermolekylära energin minimeras när partiklarna packas på det mest effektiva sättet. Det regelbundna arrangemanget på atomnivå återspeglas ofta på makroskopisk nivå. I den här modulen kommer vi att utforska några detaljer om strukturerna hos metalliska och joniska kristallina fasta ämnen och lära oss hur dessa strukturer bestäms experimentellt.

Metallernas strukturer

Vi kommer att börja vår diskussion om kristallina fasta ämnen med att betrakta elementära metaller, som är relativt enkla eftersom var och en av dem bara innehåller en typ av atom. En ren metall är ett kristallint fast ämne med metallatomer packade tätt intill varandra i ett upprepande mönster. Vissa av metallernas egenskaper i allmänhet, t.ex. deras formbarhet och duktilitet, beror till stor del på att de har identiska atomer ordnade i ett regelbundet mönster. De olika egenskaperna hos en metall jämfört med en annan beror delvis på atomernas storlek och de specifika egenskaperna hos deras rumsliga arrangemang. Vi kommer att utforska likheterna och skillnaderna mellan fyra av de vanligaste metallkristallgeometrierna i de följande avsnitten.

Metallers enhetsceller

Strukturen hos ett kristallint fast ämne, oavsett om det är en metall eller inte, beskrivs bäst genom att betrakta dess enklaste upprepande enhet, som kallas för dess enhetscell. Enhetscellen består av gitterpunkter som representerar atomernas eller jonernas placering. Hela strukturen består sedan av denna enhetscell som upprepas i tre dimensioner, vilket illustreras i figur 1.

Figur 1. En enhetscell visar placeringarna av gitterpunkter som upprepas i alla riktningar.

Låt oss börja vår undersökning av kristallgitterstruktur och enhetsceller med den mest okomplicerade strukturen och den mest grundläggande enhetscellen. För att visualisera detta kan man tänka sig att man tar ett stort antal identiska sfärer, t.ex. tennisbollar, och arrangerar dem enhetligt i en behållare. Det enklaste sättet att göra detta skulle vara att göra lager där kulorna i ett lager ligger direkt ovanför kulorna i det underliggande lagret, vilket illustreras i figur 2. Detta arrangemang kallas enkel kubisk struktur, och enhetscellen kallas enkel kubisk enhetscell eller primitiv kubisk enhetscell.

Figur 2. När metallatomer är arrangerade med sfärer i ett lager direkt över eller under sfärer i ett annat lager kallas gitterstrukturen för enkel kubisk. Observera att sfärerna är i kontakt.

I en enkel kubisk struktur är sfärerna inte packade så tätt som de skulle kunna vara, och de ”fyller” endast cirka 52 % av behållarens volym. Detta är ett relativt ineffektivt arrangemang, och endast en metall (polonium, Po) kristalliserar i en enkel kubisk struktur. Som visas i figur 3 består ett fast ämne med denna typ av arrangemang av plan (eller lager) där varje atom endast kommer i kontakt med de fyra närmaste grannarna i sitt lager; en atom direkt ovanför den i lagret ovanför; och en atom direkt under den i lagret nedanför. Det antal andra partiklar som varje partikel i ett kristallint fast ämne har kontakt med är känt som dess koordinationstal. För en poloniumatom i en enkel kubisk grupp är koordinationstalet därför sex.

Figur 3. En atom i en enkel kubisk gitterstruktur kontaktar sex andra atomer, så den har ett koordinationsnummer på sex.

I ett enkelt kubiskt gitter är enhetscellen som upprepas i alla riktningar en kub som definieras av centrumen för åtta atomer, vilket visas i figur 4. Atomer i intilliggande hörn av denna enhetscell kontaktar varandra, så kantlängden i denna cell är lika med två atomradier, eller en atomdiameter. En kubisk enhetscell innehåller endast de delar av dessa atomer som befinner sig inom den. Eftersom en atom i ett hörn av en enkel kubisk enhetscell ingår i totalt åtta enhetsceller, finns endast en åttondel av den atomen inom en specifik enhetscell. Och eftersom varje enkel kubisk enhetscell har en atom i vart och ett av sina åtta ”hörn” finns det 8 \ gånger \frac{1}{8}=1 atom inom en enkel kubisk enhetscell.

Figur 4. En enkel kubisk gittercell innehåller en åttondel av en atom i vart och ett av sina åtta hörn, så den innehåller totalt en atom.

Exempel 1: Beräkning av atomradie och densitet för metaller, del 1

Kantlängden på enhetscellen för alfapolonium är 336 pm.

1. Bestäm radien för en poloniumatom.
2. Bestäm densiteten för alfapolonium.

Visa lösning

Alphapolonium kristalliserar i en enkel kubisk enhetscell:

1. Två intilliggande Po-atomer kontaktar varandra, så kantlängden i denna cell är lika med två Po-atomradier: l=2r. Därför är Po:s radie r=\dfrac{\text{l}}{2}=\dfrac{\text{336 pm}}}{2}=\text{168 pm}.
2. Täthet ges av \text{densitet}=\dfrac{\text{massa}}{\text{volym}}. Poloniums densitet kan hittas genom att bestämma densiteten i dess enhetscell (massan i en enhetscell dividerad med volymen i enhetscellen). Eftersom en Po-enhetscell innehåller en åttondel av en Poatom i vart och ett av sina åtta hörn, innehåller en enhetscell en Poatom.

Massan av en Po-enhetscell kan hittas genom:

\text{1 Po-enhetscell}\times \dfrac{\text{1 Poatom}}{\text{1 Po-enhetscell}}\times \dfrac{\text{1 mol Po}}{6.022\times {10}^{23}\text{Po atoms}}\times \dfrac{208.998\text{g}}{\text{1 mol Po}}=3.47\times {10}^{-22}\text{g}

Volymen av en Po-enhetscell kan hittas genom:

V={l}^{3}={(336\times {10}^{-10}\text{cm})}^{3}=3.79\times {10}^{-23}{\text{cm}}}^{3}

(Observera att kantlängden konverterades från pm till cm för att få de vanliga volymenheterna för densitet.)

Därmed blir densiteten för \text{Po}=\dfrac{3.471\times {10}^{-22}\text{g}}{3.79\times {10}^{-23}{\text{cm}}^{3}}}={\text{9.16 g/cm}}^{3}

Kontrollera din inlärning

Kantlängden för enhetscellen för nickel är 0,3524 nm. Densiteten för Ni är 8,90 g/cm3. Kristalliserar nickel i en enkel kubisk struktur? Förklara.

Visa lösning

Nej. Om Ni var enkel kubisk skulle dess densitet ges av:

\text{1 Ni atom}\times \dfrac{\text{1 mol Ni}}{6.022\times {10}^{23}\text{Ni atoms}}\times \dfrac{58.693\text{g}}{\text{1 mol Ni}}=9.746\times {10}^{-23}\text{g}
V={l}^{3}={(3.524\times {10}^{-8}\text{cm})}^{3}=4.376\times {10}^{-23}{\text{cm}}^{3}

Då skulle densiteten av Ni vara =\dfrac{9.746\times {10}{-23}\text{g}}{4.376\times {10}{-23}{\text{cm}}^{3}}={\text{2.23 g/cm}}^{3}

Då Ni:s faktiska densitet inte ligger nära denna bildar Ni inte en enkel kubisk struktur.

De flesta metallkristaller är en av de fyra huvudtyperna av enhetsceller. För tillfället kommer vi att fokusera på de tre kubiska enhetscellerna: enkel kubisk (som vi redan har sett), kroppscentrerad kubisk enhetscell och ansiktscentrerad kubisk enhetscell – alla illustrerade i figur 5. (Observera att det faktiskt finns sju olika gittarsystem, varav vissa har mer än en typ av gitter, vilket ger totalt 14 olika typer av enhetsceller. Vi lämnar de mer komplicerade geometrierna till senare i den här modulen.)

Figur 5. Kubiska enhetsceller av metaller visar (i de övre figurerna) placeringarna av gitterpunkterna och (i de nedre figurerna) metallatomer placerade i enhetscellen.

Vissa metaller kristalliserar i ett arrangemang som har en kubisk enhetscell med atomer i alla hörn och en atom i mitten, som visas i figur 6. Detta kallas ett kroppscentrerat kubiskt (BCC) fast ämne. Atomerna i hörnen i en BCC-enhetscell kommer inte i kontakt med varandra utan med atomen i centrum. En BCC-enhetscell innehåller två atomer: en åttondel av en atom i vart och ett av de åtta hörnen ( 8\times \frac{1}{8}=1 atom från hörnen) plus en atom från centrum. Varje atom i denna struktur berör fyra atomer i lagret ovanför den och fyra atomer i lagret under den. En atom i en BCC-struktur har alltså ett koordinationsnummer på åtta.

Figur 6. I en kroppscentrerad kubisk struktur rör atomerna i ett visst lager inte vid varandra. Varje atom berör fyra atomer i lagret ovanför den och fyra atomer i lagret under den.

Atomer i BCC-arrangemang är mycket effektivare packade än i en enkel kubisk struktur och upptar ungefär 68 % av den totala volymen. Isomorfa metaller med en BCC-struktur omfattar K, Ba, Cr, Mo, W och Fe vid rumstemperatur. (Element eller föreningar som kristalliserar med samma struktur sägs vara isomorfa.)

Många andra metaller, t.ex. aluminium, koppar och bly, kristalliserar i ett arrangemang som har en kubisk enhetscell med atomer i alla hörn och i mitten av varje sida, vilket illustreras i figur 7. Detta arrangemang kallas för ett ansiktecentrerat kubiskt (FCC) fast ämne. En FCC-enhetscell innehåller fyra atomer: en åttondel av en atom vid vart och ett av de åtta hörnen ( 8\times \frac{1}{8}=1 atom från hörnen) och en halv atom på var och en av de sex sidorna (6\times \frac{1}{2}=3 atomer från sidorna). Atomerna i hörnen berör atomerna i centrum av de angränsande ytorna längs kubens diagonaler. Eftersom atomerna befinner sig på identiska gitterpunkter har de identiska miljöer.

Figur 7. Ett ytcentrerat kubiskt fast ämne har atomer i hörnen och, som namnet antyder, i mitten av ytorna i dess enhetsceller.

Atomer i ett FCC-arrangemang är packade så tätt intill varandra som möjligt, med atomer som upptar 74 % av volymen. Denna struktur kallas också cubic closest packing (CCP). I CCP finns det tre upprepade lager av hexagonalt arrangerade atomer. Varje atom har kontakt med sex atomer i sitt eget lager, tre i lagret ovanför och tre i lagret under. I detta arrangemang berör varje atom 12 nära grannar och har därför ett koordinationsnummer på 12. Att FCC- och CCP-arrangemangen är likvärdiga är kanske inte omedelbart uppenbart, men varför de faktiskt är samma struktur illustreras i figur 8.

Figur 8. Ett CCP-arrangemang består av tre upprepade lager (ABCABC…) av hexagonalt arrangerade atomer. Atomer i en CCP-struktur har ett koordinationstal på 12 eftersom de har kontakt med sex atomer i sitt lager, plus tre atomer i lagret ovanför och tre atomer i lagret under. Genom att vrida vårt perspektiv kan vi se att en CCP-struktur har en enhetscell med en yta som innehåller en atom från lager A i ett hörn, atomer från lager B över en diagonal (i två hörn och i mitten av ytan) och en atom från lager C i det återstående hörnet. Detta är detsamma som ett ytcentrerat kubiskt arrangemang.

Då tätare packning maximerar de totala attraktionskrafterna mellan atomerna och minimerar den totala intermolekylära energin, packar atomerna i de flesta metaller på detta sätt. Vi finner två typer av närmast packning i enkla metalliska kristallina strukturer: CCP, som vi redan har träffat på, och hexagonal närmast packning (HCP) som visas i figur 9. Båda består av upprepade lager av hexagonalt arrangerade atomer. I båda typerna är ett andra lager (B) placerat på det första lagret (A) så att varje atom i det andra lagret är i kontakt med tre atomer i det första lagret. Det tredje lagret placeras på ett av två sätt. I HCP ligger atomer i det tredje lagret direkt ovanför atomer i det första lagret (dvs. det tredje lagret är också av typ A), och staplingen består av omväxlande nära packade lager av typ A och typ B (dvs. ABABAB⋯). I CCP ligger atomer i det tredje lagret inte över atomer i något av de två första lagren (dvs. det tredje lagret är av typ C), och stapeln består av omväxlande nära packade lager av typ A, typ B och typ C (dvs. ABCABCABCABC⋯). Ungefär två tredjedelar av alla metaller kristalliserar i närmast packade lager med koordinationsnummer 12. Metaller som kristalliserar i en HCP-struktur är Cd, Co, Li, Mg, Na och Zn, och metaller som kristalliserar i en CCP-struktur är Ag, Al, Ca, Cu, Ni, Pb och Pt.

Figur 9. I båda typerna av närmaste packning packas atomerna så kompakt som möjligt. Hexagonal närmast packning består av två omväxlande lager (ABABABAB…). Kubisk närmsta packning består av tre alternerande lager (ABCABCABCABC…).

Exempel 2: Beräkning av atomradie och densitet för metaller, del 2

Calcium kristalliserar i en ytcentrerad kubisk struktur. Kantlängden för dess enhetscell är 558,8 pm.

1. Vad är atomradien för Ca i denna struktur?
2. Beräkna densiteten för Ca.

Visa lösningen

Del 1

I en FCC-struktur kontaktar Ca-atomerna varandra tvärs över ytans diagonal, så diagonalens längd är lika med fyra Ca-atomradier (d = 4r). Två intilliggande kanter och diagonalen på ytan bildar en rät triangel, där längden på varje sida är lika med 558,8 pm och längden på hypotenusan är lika med fyra Ca-atomära radier:

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}^{2}\longrightarrow {(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}={(4r)}^{2}

Solving this gives r=\sqrt{\dfrac{{(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}}}{16}}}=\text{197.6 pmg för en Ca-radie}.

Del 2

Densiteten ges av \text{densitet}=\dfrac{\text{massa}}{\text{volym}}. Kalciums densitet kan hittas genom att bestämma densiteten i dess enhetscell: till exempel massan som ingår i en enhetscell dividerad med volymen i enhetscellen. En ytcentrerad Ca-enhetscell har en åttonde atom i vart och ett av de åtta hörnen \left(8\times \dfrac{1}{8}=1\text{atom}\right) och en halv atom på var och en av de sex ytorna \left(6\times \dfrac{1}{2}=3\text{atom}\right), vilket ger totalt fyra atomer i enhetscellen.

Massan av enhetscellen kan hittas genom:

\text{1 Ca unit cell}\times \dfrac{\text{4 Ca atoms}}{\text{1 Ca unit cell}}\times \dfrac{\text{1 mol Ca}}{6.022\times {10}^{23}\text{Ca atoms}}\times \dfrac{40.078\text{g}}{\text{1 mol Ca}}=2.662\times {10}^{-22}\text{g}

Volymen av en Ca-enhetscell kan hittas genom:

V={a}^{3}={(558.8\times {10}^{-10}\text{cm})}^{3}=1.745\times {10}^{-22}{\text{cm}}}^{3}

(Observera att kantlängden konverterades från pm till cm för att få de vanliga volymenheterna för densitet.)

Då blir densiteten av \text{Ca}=\dfrac{2.662\times {10}^{-22}\text{g}}{1.745\times {10}^{-22}{\text{cm}}^{3}}}={\text{1.53 g/cm}}^{3}

Kontrollera din inlärning

Silver kristalliserar i en FCC-struktur. Kantlängden för dess enhetscell är 409 pm.

1. Vad är atomradien för Ag i denna struktur?
2. Beräkna densiteten för Ag.

Visa lösningar

1. 144 pm
2. 10.5 g/cm3

I allmänhet definieras en enhetscell av längderna på tre axlar (a, b och c) och vinklarna (α, β och γ) mellan dem, vilket illustreras i figur 10. Axlarna definieras som längderna mellan punkterna i rymdgittret. Följaktligen förenar enhetscellens axlar punkter med identiska miljöer.

Figur 10. En enhetscell definieras av längderna på dess tre axlar (a, b och c) och vinklarna (α, β och γ) mellan axlarna.

Det finns sju olika gittarsystem, varav vissa har mer än en typ av gitter, för totalt fjorton olika enhetsceller, som har de former som visas i figur 11.

Figur 11. Det finns sju olika gittarsystem och 14 olika enhetsceller.

Strukturerna hos joniska kristaller

Ioniska kristaller består av två eller flera olika sorters joner som vanligtvis har olika storlekar. Packningen av dessa joner i en kristallstruktur är mer komplex än packningen av metallatomer som har samma storlek.

De flesta enatomiga joner beter sig som laddade sfärer, och deras dragningskraft på joner med motsatt laddning är densamma i alla riktningar. Följaktligen uppstår stabila strukturer för joniska föreningar (1) när joner med en laddning omges av så många joner som möjligt med motsatt laddning och (2) när katjoner och anjoner är i kontakt med varandra. Strukturerna bestäms av två huvudfaktorer: jonernas relativa storlek och förhållandet mellan antalet positiva och negativa joner i föreningen.

Figur 12. Kationer kan ockupera två typer av hål mellan anjoner: oktaedriska hål eller tetraedriska hål.

I enkla jonstrukturer finner vi vanligen anjonerna, som normalt är större än katjonerna, arrangerade i en närmast packad rad. (Som vi sett tidigare gör fler elektroner som dras till samma kärna anjoner större och färre elektroner som dras till samma kärna gör katjoner mindre jämfört med de atomer som de bildas av). De mindre katjonerna upptar vanligen en av två typer av hål (eller mellanrum) som återstår mellan anjonerna. Det mindre av hålen finns mellan tre anjoner i ett plan och en anjon i ett angränsande plan. De fyra anjoner som omger detta hål är placerade i hörnen av en tetraeder, så hålet kallas för ett tetraederhål. Den större typen av hål finns i mitten av sex anjoner (tre i ett plan och tre i ett angränsande plan) som är placerade i hörnen av en oktaeder; detta kallas ett oktaedriskt hål. Figur 12 illustrerar båda dessa typer av hål.

Avhängigt av katjonernas och anjonernas relativa storlek kan katjonerna i en jonisk förening inta tetraeder- eller oktaederhål, vilket illustreras i figur 13. Relativt små katjoner upptar tetraedriska hål och större katjoner upptar oktaedriska hål. Om katjonerna är för stora för att rymmas i de oktaedriska hålen kan anjonerna anta en mer öppen struktur, t.ex. en enkel kubisk grupp. De större katjonerna kan då ockupera de större kubiska hålen som möjliggörs av det öppnare avståndet.

Figur 13. En katjons storlek och formen på det hål som upptas av föreningen är direkt relaterade.

Det finns två tetraedriska hål för varje anjon i antingen en HCP- eller CCP-mall av anjoner. En förening som kristalliserar i en närmast packad anjoner med katjoner i de tetraedriska hålen kan ha ett maximalt katjon/anjon-förhållande på 2:1; alla de tetraedriska hålen är fyllda vid detta förhållande. Exempel är Li2O, Na2O, Li2S och Na2S. Föreningar med ett förhållande på mindre än 2:1 kan också kristallisera i en närmast packad rad av anjoner med katjoner i de tetraedriska hålen, om de joniska storlekarna passar. I dessa föreningar förblir dock en del av de tetraedriska hålen lediga.

Förhållandet mellan oktaedriska hål och anjoner i antingen en HCP- eller CCP-struktur är 1:1. Således kan föreningar med katjoner i oktaedriska hål i en närmast packad rad av anjoner ha ett maximalt katjon/anjon-förhållande på 1:1. I NiO, MnS, NaCl och KH, till exempel, är alla oktaedriska hål fyllda. Förhållanden på mindre än 1:1 observeras när några av de oktaedriska hålen förblir tomma.

I en enkel kubisk grupp av anjoner finns det ett kubiskt hål som kan upptas av en katjon för varje anjon i gruppen. I CsCl, och i andra föreningar med samma struktur, är alla kubiska hål upptagna. Hälften av de kubiska hålen är upptagna i SrH2, UO2, SrCl2 och CaF2.

Olika typer av jonföreningar kristalliserar ofta i samma struktur när de relativa storlekarna av deras joner och deras stökiometri (de två viktigaste egenskaperna som bestämmer strukturen) är liknande.

Enhetsceller för joniska föreningar

Många joniska föreningar kristalliserar med kubiska enhetsceller, och vi kommer att använda dessa föreningar för att beskriva de allmänna egenskaperna hos joniska strukturer.

När en jonisk förening är sammansatt av katjoner och anjoner av liknande storlek i ett 1:1-förhållande bildar den vanligtvis en enkel kubisk struktur. Cesiumklorid, CsCl, (illustrerad i figur 14) är ett exempel på detta, där Cs+ och Cl- har radier på 174 pm respektive 181 pm. Vi kan se detta som att kloridjoner bildar en enkel kubisk enhetscell med en cesiumjon i centrum, eller att cesiumjoner bildar en enhetscell med en kloridjon i centrum, eller att enkla kubiska enhetsceller som bildas av Cs+-joner överlappar enhetsceller som bildas av Cl-joner. Cesiumjoner och kloridjoner berör varandra längs enhetscellernas diagonaler. En cesiumjon och en kloridjon finns i varje enhetscell, vilket ger den stökiometri l:l som krävs enligt formeln för cesiumklorid. Observera att det inte finns någon gitterpunkt i cellens centrum, och CsCl är inte en BCC-struktur eftersom en cesiumjon inte är identisk med en kloridjon.

Figur 14. Joniska föreningar med lika stora katjoner och anjoner, till exempel CsCl, bildar vanligtvis en enkel kubisk struktur. De kan beskrivas av enhetsceller med antingen katjoner i hörnen eller anjoner i hörnen.

Vi har sagt att placeringen av gitterpunkterna är godtycklig. Detta illustreras av en alternativ beskrivning av CsCl-strukturen där gitterpunkterna är placerade i cesiumjonernas centrum. I denna beskrivning är cesiumjonerna placerade på gitterpunkterna i cellens hörn och kloridjonen är placerad i cellens centrum. De två enhetscellerna är olika, men de beskriver identiska strukturer.

När en jonisk förening består av ett 1:1-förhållande av katjoner och anjoner som skiljer sig avsevärt i storlek, kristalliserar den vanligtvis med en FCC-enhetscell, som den som visas i figur 15. Natriumklorid, NaCl, är ett exempel på detta, där Na+ och Cl- har radier på 102 pm respektive 181 pm. Vi kan se detta som att kloridjoner bildar en FCC-cell, med natriumjoner placerade i de oktaedriska hålen i mitten av cellkanterna och i mitten av cellen. Natrium- och kloridjonerna rör vid varandra längs cellkanterna. Enhetscellen innehåller fyra natriumjoner och fyra kloridjoner, vilket ger den stökiometri på 1:1 som krävs för formeln NaCl.

Figur 15. Joniska föreningar med anjoner som är mycket större än katjoner, till exempel NaCl, bildar vanligtvis en FCC-struktur. De kan beskrivas av FCC-enhetsceller med katjoner i de oktaedriska hålen.

Den kubiska formen av zinksulfid, zinkblende, kristalliserar också i en FCC-enhetscell, vilket illustreras i figur 16. Denna struktur innehåller sulfidjoner på gitterpunkterna i ett FCC-gitter. (Sulfidjonernas placering är identisk med kloridjonernas placering i natriumklorid). Radien för en zinkjon är endast cirka 40 % av radien för en sulfidjon, så dessa små Zn2+ -joner är placerade i alternerande tetraederhål, det vill säga i ena halvan av tetraederhålen. Det finns fyra zinkjoner och fyra sulfidjoner i enhetscellen, vilket ger den empiriska formeln ZnS.

Figur 16. ZnS, zinksulfid (eller zinkblände) bildar en FCC-enhetscell med sulfidjoner vid gitterpunkterna och mycket mindre zinkjoner som upptar hälften av de tetraedriska hålen i strukturen.

En kalciumfluorid-enhetscell, som den som visas i figur 17, är också en FCC-enhetscell, men i det här fallet är katjonerna placerade vid gitterpunkterna; motsvarande kalciumjoner är placerade vid gitterpunkterna i ett FCC-gitter. Alla tetraedriska platser i FCC-arrayet av kalciumjoner är upptagna av fluoridjoner. Det finns fyra kalciumjoner och åtta fluoridjoner i en enhetscell, vilket ger ett kalcium- och fluorförhållande på 1:2, vilket krävs enligt den kemiska formeln CaF2. En närmare granskning av figur 17 visar en enkel kubisk grupp av fluoridjoner med kalciumjoner i ena halvan av de kubiska hålen. Strukturen kan inte beskrivas i termer av ett rymdgitter av punkter på fluoridjonerna eftersom fluoridjonerna inte alla har identiska miljöer. De fyra kalciumjonernas orientering kring fluoridjonerna skiljer sig åt.

Figur 17. Kalciumfluorid, CaF2, bildar en FCC-enhetscell med kalciumjoner (gröna) vid gitterpunkterna och fluoridjoner (röda) som upptar alla tetraederplatser mellan dem.

Beräkning av joniska radier

Om vi känner till kantlängden för en enhetscell i en jonisk förening och jonernas position i cellen kan vi beräkna joniska radier för jonerna i föreningen om vi gör antaganden om enskilda joners form och kontakter.

Exempel 5: Beräkning av joniska radier

Kantlängden för enhetscellen hos LiCl (NaCl-liknande struktur, FCC) är 0.514 nm eller 5,14 Å. Om man antar att litiumjonen är tillräckligt liten så att kloridjonerna är i kontakt, som i figur 15, beräkna då jonradien för kloridjonen.

Anmärkning: Längdenheten angström, Å, används ofta för att representera dimensioner på atomär skala och motsvarar 10-10 m.

Visa lösning

På ytan av en LiCl-enhetscell har kloridjoner kontakt med varandra över ytans diagonal:

Om vi ritar en rätvinklig triangel på enhetscellens yta ser vi att diagonalens längd är lika med fyra kloridradier (en radie från varje kloridhörn och en diameter – som är lika med två radier – från kloridjonen i mitten av ytan), så d = 4r. Från Pythagoras sats har vi:

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}}^{2}

vilket ger:

\left(0.514\text{ nm}\right)^{2}+\left(0.514\text{ nm}\right)^{2}={\left(4r\right)}^{2}=16{r}^{2}

Solving this gives:

r=\sqrt{\dfrac{{(0.514\text{nm})}^{2}+{(0.514\text{nm})}^{2}}{16}}=\text{0.182 nm} (1,82 Å) för en Cl- radie

Kontrollera din inlärning

Kantlängden på enhetscellen för KCl (NaCl-liknande struktur, FCC) är 6,28 Å. Beräkna kaliumjonens radie om man utgår från att det finns en anjon-kation kontakt längs cellkanten. Kloridjonens radie är 1,82 Å.

Visa lösning

Kaliumjonens radie är 1,33 Å.

Det är viktigt att inse att värdena för joniska radier beräknade från enhetscellernas kantlängder är beroende av ett flertal antaganden, t.ex. en perfekt sfärisk form för jonerna, som i bästa fall är approximationer. Därför är sådana beräknade värden i sig själva ungefärliga och jämförelser kan inte drivas för långt. Icke desto mindre har denna metod visat sig vara användbar för att beräkna jonradier från experimentella mätningar såsom röntgenkristallografiska bestämningar.

Röntgenkristallografi

Enhetscellens storlek och atomernas arrangemang i en kristall kan bestämmas genom mätningar av röntgenstrålarnas diffraktion av kristallen, så kallad röntgenkristallografi. Diffraktion är den förändring av färdriktningen som en elektromagnetisk våg upplever när den möter en fysisk barriär vars dimensioner är jämförbara med ljusets våglängd. Röntgenstrålar är elektromagnetisk strålning med våglängder som är ungefär lika långa som avståndet mellan närliggande atomer i kristaller (i storleksordningen några Å).

När en stråle av monokromatisk röntgenstrålning träffar en kristall, sprids dess strålar i alla riktningar av atomerna i kristallen. När spridda vågor som färdas i samma riktning möter varandra genomgår de interferens, en process genom vilken vågorna kombineras för att ge antingen en ökning eller minskning av amplituden (intensiteten) beroende på i vilken utsträckning de kombinerande vågornas maxima är separerade (se figur 18).

Figur 18. Ljusvågor som upptar samma utrymme upplever interferens och kombineras för att ge vågor med större (a) eller mindre (b) intensitet, beroende på avståndet mellan deras maxima och minima.

När röntgenstrålar med en viss våglängd, λ, sprids av atomer i intilliggande kristallplan som är åtskilda av ett avstånd, d, kan de genomgå konstruktiva interferenser när skillnaden mellan avstånden som de två vågorna har tillryggalagt innan de kombineras är en helhetsfaktor, n, av våglängden. Detta villkor är uppfyllt när den diffrakterade strålens vinkel, θ, är relaterad till våglängden och det interatomära avståndet med ekvationen:

n{\lambda }=2d\text{sin}\theta

Denna relation är känd som Bragg-ekvationen till ära av W. H. Bragg, den engelske fysiker som först förklarade detta fenomen. Figur 19 illustrerar två exempel på diffrakterade vågor från samma två kristallplan. Figuren till vänster visar vågor som diffrakteras i Braggvinkeln, vilket resulterar i konstruktiv interferens, medan figuren till höger visar diffraktion och en annan vinkel som inte uppfyller Braggvillkoret, vilket resulterar i destruktiv interferens.

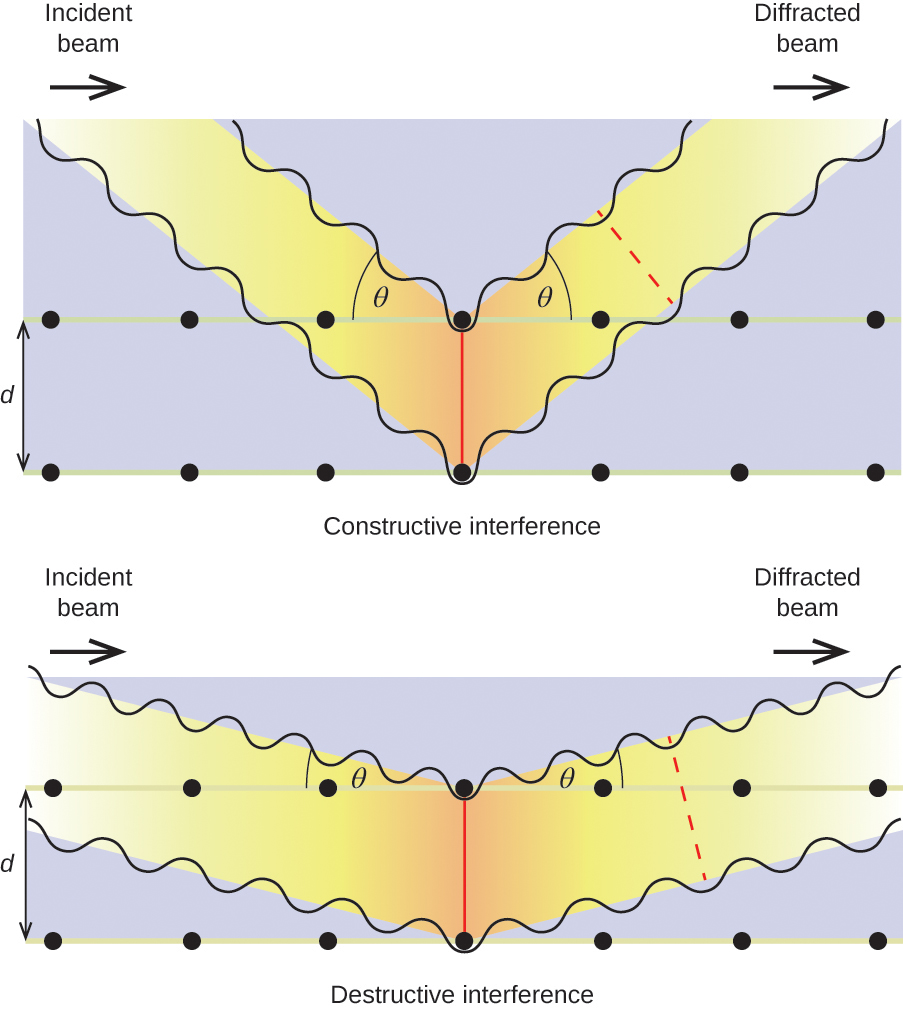
Figur 19. Diffraktionen av röntgenstrålar som sprids av atomerna i en kristall gör det möjligt att bestämma avståndet mellan atomerna. Den övre bilden visar konstruktiv interferens mellan två spridda vågor och en resulterande diffrakterad våg med hög intensitet. Den nedre bilden visar destruktiv interferens och en diffrakterad våg med låg intensitet.

En röntgendiffraktometer, som den som illustreras i figur 20, kan användas för att mäta de vinklar vid vilka röntgenstrålar diffrakteras när de interagerar med en kristall enligt beskrivningen ovan. Utifrån sådana mätningar kan Bragg-ekvationen användas för att beräkna avstånden mellan atomer, vilket visas i följande exempelövning.

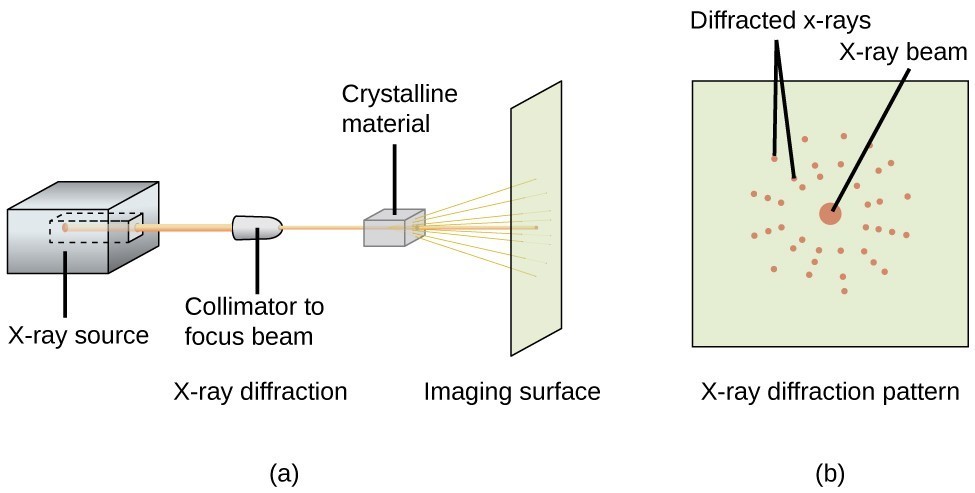
Figur 20. I en diffraktometer (a) träffar en stråle av röntgenstrålar ett kristallint material och ger upphov till ett röntgendiffraktionsmönster (b) som kan analyseras för att bestämma kristallstrukturen.

Du kan se transkriptet till ”Celebrating Crystallography – An animated adventure” här (öppnas i nytt fönster).

Porträtt av en kemist: Röntgenkristallograf Rosalind Franklin

Figur 21. Den här illustrationen visar en röntgendiffraktionsbild som liknar den som Franklin hittade i sin forskning. (kredit: National Institutes of Health)

Upptäckten av DNA:s struktur 1953 av Francis Crick och James Watson är en av de stora bedrifterna i vetenskapshistorien. De tilldelades 1962 Nobelpriset i fysiologi eller medicin tillsammans med Maurice Wilkins, som gav experimentella bevis för DNA:s struktur. Den brittiska kemisten Rosalind Franklin gav ovärderliga bidrag till denna monumentala prestation genom sitt arbete med att mäta röntgendiffraktionsbilder av DNA. Tidigt i sin karriär visade sig Franklins forskning om kols struktur vara till hjälp för den brittiska krigsmakten. Efter att ha flyttat sitt fokus till biologiska system i början av 1950-talet upptäckte Franklin och doktoranden Raymond Gosling att DNA består av två former: en lång, tunn fiber som bildas när den är våt (typ ”B”) och en kort, bred fiber som bildas när den torkas (typ ”A”). Hennes röntgendiffraktionsbilder av DNA (figur 21) gav den avgörande information som gjorde det möjligt för Watson och Crick att bekräfta att DNA bildar en dubbelspiral och att fastställa detaljer om dess storlek och struktur.

Franklin utförde också banbrytande forskning om virus och det RNA som innehåller deras genetiska information och avslöjade ny information som radikalt förändrade kunskapsmassan på området. Efter att ha drabbats av äggstockscancer fortsatte Franklin att arbeta fram till sin död 1958 vid 37 års ålder. Bland många postuma erkännanden av hennes arbete bytte Chicago Medical School of Finch University of Health Sciences 2004 namn till Rosalind Franklin University of Medicine and Science och antog en bild av hennes berömda röntgendiffraktionsbild av DNA som sin officiella universitetslogotyp.

Glossar

kroppscentrerad kubisk (BCC) fast substans: kristallin struktur som har en kubisk enhetscell med gitterpunkter vid hörnen och i cellens centrum

kroppscentrerad kubisk enhetscell: Det är en kub som innehåller gitterpunkter i varje hörn och i kubens centrum

Bragg-ekvation: Ekvation som relaterar de vinklar i vilka röntgenstrålar diffrakteras av atomerna i en kristall

Koordineringsnummer: Antal atomer som ligger närmast en viss atom i en kristall eller den centrala metallatomen i ett komplex

Cubic Closest Packing (CCP): Kristallstruktur: Kristallstruktur där plan av tätt packade atomer eller joner är staplade som en serie av tre alternerande lager med olika relativa orienteringar (ABC)

diffraktion: En kristallin struktur där de närmaste atomerna eller jonerna är staplade som en serie av tre alternerande lager med olika relativa orienteringar (ABC): Omdirigering av elektromagnetisk strålning som sker när den möter en fysisk barriär av lämpliga dimensioner

Flänscentrerad kubisk (FCC) fast ämne: Kristallin struktur som består av en kubisk enhetscell med gitterpunkter på hörnen och i mitten av varje yta

Flänscentrerad kubisk enhetscell: Det är en kub med gitterpunkter i varje hörn och i mitten av varje sida

hexagonal närmast packning (HCP): Kristallin struktur där tätt packade lager av atomer eller joner är staplade som en serie av två alternerande lager med olika relativa orienteringar (AB)

Hål: En kristallin struktur som består av två lager som är tätt packade och har olika orienteringar (AB)

: (även interstice) utrymme mellan atomer i en kristall

isomorf: har samma kristallina struktur

oktaedrisk hål: öppet utrymme i en kristall i mitten av sex partiklar som är placerade i hörnen av en oktaeder

en enkel kubisk enhetscell: (även primitiv kubisk enhetscell) enhetscell i den enkla kubiska strukturen

simpel kubisk struktur: kristallin struktur med en kubisk enhetscell med gitterpunkter endast i hörnen

utrymningsgitter: alla punkter i en kristall som har identiska miljöer

tetraederhål:

Enhetscell: Den minsta delen av ett rymdgitter som upprepas i tre dimensioner för att bilda hela gittret

Röntgenkristallografi: Experimentell teknik för att bestämma avstånd mellan atomer i en kristall genom att mäta de vinklar i vilka röntgenstrålar diffrakteras när de passerar genom kristallen