- Lärandemål
- Tryck och temperatur: Gay-Lussacs lag
- Volym och temperatur: Charles lag
- Volym och tryck: Boyles lag
- Chemistry in Action: Vad gör du ungefär 20 gånger per minut i hela ditt liv, utan avbrott och ofta utan att vara medveten om det? Svaret är naturligtvis andning, eller andning. Hur fungerar det? Det visar sig att gaslagarna är tillämpliga här. Dina lungor tar in gas som din kropp behöver (syre) och gör sig av med avfallsgas (koldioxid). Lungorna består av svampig, stretchig vävnad som expanderar och drar ihop sig när du andas. När du andas in drar diafragman och de interkostala musklerna (musklerna mellan revbenen) ihop sig, vilket utvidgar brösthålan och gör lungvolymen större. Volymökningen leder till en minskning av trycket (Boyles lag). Detta gör att luften strömmar in i lungorna (från högt tryck till lågt tryck). När du andas ut är processen omvänd: Ditt diafragma och dina revbensmuskler slappnar av, brösthålan drar ihop sig och lungvolymen minskar, vilket leder till att trycket ökar (Boyles lag igen) och luft strömmar ut ur lungorna (från högt tryck till lågt tryck). Du andas sedan in och ut igen, och igen, och upprepar denna cykel enligt Boyles lag resten av ditt liv (figur 7). Figur 7. Andningen sker på grund av att expanderande och krympande lungvolym skapar små tryckskillnader mellan dina lungor och din omgivning, vilket gör att luft dras in i och tvingas ut ur lungorna.
- Mol av gas och volym: Avogadros lag
- Glossar
Lärandemål
I slutet av detta avsnitt kommer du att kunna:
- Identifiera de matematiska sambanden mellan gasers olika egenskaper
- Använda den kombinerade gaslagen, och relaterade gaslagar, för att beräkna värdena för olika gasegenskaper under specificerade förhållanden
Under 1600-talet och framför allt 1700-talet, drivna både av en önskan att förstå naturen och en strävan efter att tillverka ballonger som de kunde flyga i (figur 1), fastställde ett antal vetenskapsmän sambanden mellan gasers makroskopiska fysikaliska egenskaper, det vill säga tryck, volym, temperatur och gasmängd. Även om deras mätningar inte var exakta med dagens mått mätt kunde de fastställa de matematiska sambanden mellan par av dessa variabler (t.ex. tryck och temperatur, tryck och volym) som gäller för en idealgas – en hypotetisk konstruktion som verkliga gaser närmar sig under vissa förhållanden. Så småningom kombinerades dessa enskilda lagar till en enda ekvation – den ideala gaslagen – som relaterar gasmängder för gaser och som är ganska exakt för låga tryck och måttliga temperaturer. Vi kommer att betrakta den viktigaste utvecklingen av de enskilda förhållandena (av pedagogiska skäl inte helt i historisk ordning) och sedan sätta ihop dem i lagen om den ideala gasen.

Figur 1. År 1783 skedde den första a) vätgasfyllda ballongflygningen, b) bemannade varmluftsballongflygningen och c) bemannade vätgasfyllda ballongflygningen. När den vätefyllda ballongen som avbildas i a) landade, rapporterades det att de skrämda byborna i Gonesse förstörde den med högafflar och knivar. Uppskjutningen av den senare uppges ha setts av 400 000 personer i Paris.
Tryck och temperatur: Gay-Lussacs lag
Föreställ dig att du fyller en styv behållare som är fäst vid en tryckmätare med gas och sedan förseglar behållaren så att ingen gas kan flyga ut. Om behållaren kyls ner blir gasen i behållaren också kallare och man ser att trycket sjunker. Eftersom behållaren är stel och tätt försluten förblir både volymen och antalet mol gas konstant. Om vi värmer upp klotet blir gasen inuti varmare (figur 2) och trycket ökar.

Figur 2. Temperaturens effekt på gastrycket: När värmeplattan är avstängd är trycket på gasen i sfären relativt lågt. När gasen värms upp ökar trycket på gasen i sfären.
Detta förhållande mellan temperatur och tryck observeras för alla gasprover som är instängda i en konstant volym. Ett exempel på experimentella tryck-temperaturdata visas för ett luftprov under dessa förhållanden i figur 3. Vi finner att temperatur och tryck är linjärt relaterade, och om temperaturen är på kelvinskalan är P och T direkt proportionella (återigen när volym och mol av gasen hålls konstanta); om temperaturen på kelvinskalan ökar med en viss faktor ökar gastrycket med samma faktor.
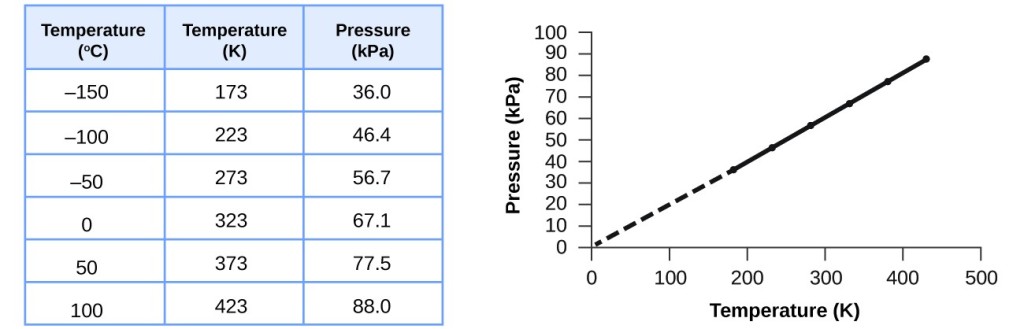
Figur 3. För en konstant volym och mängd luft är trycket och temperaturen direkt proportionella, förutsatt att temperaturen anges i kelvin. (Mätningar kan inte göras vid lägre temperaturer på grund av kondensering av gasen). När denna linje extrapoleras till lägre tryck når den ett tryck på 0 vid -273 °C, vilket är 0 på kelvinskalan och den lägsta möjliga temperaturen, kallad den absoluta nollpunkten.
Guillaume Amontons var den förste som empiriskt fastställde sambandet mellan trycket och temperaturen hos en gas (~1700), och Joseph Louis Gay-Lussac fastställde sambandet mer exakt (~1800). På grund av detta är P-T-förhållandet för gaser känt som antingen Gay-Lussacs lag eller Amontons lag. Under båda benämningarna säger den att trycket i en given mängd gas är direkt proportionellt mot dess temperatur på Kelvinskalan när volymen hålls konstant. Matematiskt kan detta skrivas:
\large P\propto T
\large P=\text{konstant}\times T
\large P=k\times T
där ∝ betyder ”är proportionell mot”, och k är en proportionalitetskonstant som beror på gasens identitet, mängd och volym.
\large\frac{{P}_{1}}{{T}_{1}}}=\frac{{P}_{2}}}{{T}_{2}}}
Denna ekvation är användbar för tryck-temperaturberäkningar för en innesluten gas vid konstant volym. Observera att temperaturerna måste vara på kelvinskalan för alla gaslagberäkningar (0 på kelvinskalan och den lägsta möjliga temperaturen kallas absolut nollpunkt). (Observera också att det finns minst tre sätt att beskriva hur trycket hos en gas förändras när dess temperatur förändras: Vi kan använda en tabell med värden, en graf eller en matematisk ekvation.)
Volym och temperatur: Charles lag
Om vi fyller en ballong med luft och förseglar den innehåller ballongen en viss mängd luft vid atmosfäriskt tryck, låt oss säga 1 atm. Om vi placerar ballongen i ett kylskåp blir gasen inuti kall och ballongen krymper (även om både mängden gas och trycket förblir konstant). Om vi gör ballongen mycket kall kommer den att krympa mycket, och den expanderar igen när den värms upp.
Denna video visar hur kylning och uppvärmning av en gas får dess volym att minska respektive öka.
Dessa exempel på temperaturens effekt på volymen av en given mängd av en innesluten gas vid konstant tryck gäller generellt: Volymen ökar när temperaturen ökar och minskar när temperaturen minskar. Volym-temperaturdata för ett 1 mol-prov av metangas vid 1 atm listas och visas grafiskt i figur 4.

Figur 4. Volymen och temperaturen är linjärt relaterade för 1 mol metangas vid ett konstant tryck på 1 atm. Om temperaturen anges i kelvin är volym och temperatur direkt proportionella. Linjen stannar vid 111 K eftersom metan blir flytande vid denna temperatur; när den extrapoleras skär den grafernas ursprung, vilket representerar en temperatur på absolut noll.
Sambandet mellan volymen och temperaturen för en given mängd gas vid konstant tryck är känt som Charles lag som ett erkännande av den franske vetenskapsmannen och ballongflygningspionjären Jacques Alexandre César Charles. Enligt Charles lag är volymen av en given mängd gas direkt proportionell mot dess temperatur på Kelvinskalan när trycket hålls konstant.
Matematiskt kan detta skrivas som:
\large V\propto T
\large V=\text{konstant}\cdot T
\large V=k\cdot T
med k som en proportionalitetskonstant som beror på gasens mängd och tryck.
\large\frac{{V}_{1}}{{T}_{1}}}=\frac{{V}_{2}}}{{T}_{2}}}
Volym och tryck: Boyles lag
Om vi delvis fyller en lufttät spruta med luft innehåller sprutan en viss mängd luft vid konstant temperatur, säg 25 °C. Om vi långsamt trycker in kolven samtidigt som temperaturen hålls konstant, komprimeras gasen i sprutan till en mindre volym och trycket ökar; om vi drar ut kolven ökar volymen och trycket minskar. Detta exempel på hur volymen påverkar trycket i en given mängd av en innesluten gas gäller i allmänhet. Om man minskar volymen av en innesluten gas ökar trycket, och om man ökar volymen minskar trycket. Om volymen ökar med en viss faktor minskar trycket med samma faktor och vice versa. Volym-trycksdata för ett luftprov vid rumstemperatur visas grafiskt i figur 5.

Figur 5. När en gas upptar en mindre volym utövar den ett högre tryck; när den upptar en större volym utövar den ett lägre tryck (förutsatt att gasmängden och temperaturen inte ändras). Eftersom P och V är omvänt proportionella är grafen 1/P mot V linjär.
Tryck och volym är inte direkt proportionella till varandra, till skillnad från P-T- och V-T-sambanden. Istället uppvisar P och V omvänt proportionalitet: En ökning av trycket resulterar i en minskning av gasens volym. Matematiskt kan detta skrivas:
\stor P\propto 1\text{/}V\text{ eller }P=k\cdot 1\text{/}V\text{ eller }P\cdot V=k\text{ eller }{P}_{1}{V}_{1}={P}_{2}{V}_{2}
med k som en konstant. Grafiskt visas detta förhållande genom den räta linje som uppstår när man plottar inversen av trycket \large\left(\frac{1}{P}\right) mot volymen (V), eller inversen av volymen \large\left(\frac{1}{V}\right) mot trycket (V). Grafer med krökta linjer är svåra att läsa exakt vid låga eller höga värden på variablerna, och de är svårare att använda för att anpassa teoretiska ekvationer och parametrar till experimentella data. Av dessa skäl försöker forskare ofta hitta ett sätt att ”linjärisera” sina data. Om vi plottar P mot V får vi en hyperbel (se figur 6).
Sambandet mellan volymen och trycket för en given mängd gas vid konstant temperatur publicerades för första gången av den engelske naturfilosofen Robert Boyle för över 300 år sedan. Det sammanfattas i det uttalande som nu är känt som Boyles lag: Volymen av en given mängd gas som hålls vid konstant temperatur är omvänt proportionell mot det tryck under vilket den mäts.
Chemistry in Action: Vad gör du ungefär 20 gånger per minut i hela ditt liv, utan avbrott och ofta utan att vara medveten om det? Svaret är naturligtvis andning, eller andning. Hur fungerar det? Det visar sig att gaslagarna är tillämpliga här. Dina lungor tar in gas som din kropp behöver (syre) och gör sig av med avfallsgas (koldioxid). Lungorna består av svampig, stretchig vävnad som expanderar och drar ihop sig när du andas. När du andas in drar diafragman och de interkostala musklerna (musklerna mellan revbenen) ihop sig, vilket utvidgar brösthålan och gör lungvolymen större. Volymökningen leder till en minskning av trycket (Boyles lag). Detta gör att luften strömmar in i lungorna (från högt tryck till lågt tryck). När du andas ut är processen omvänd: Ditt diafragma och dina revbensmuskler slappnar av, brösthålan drar ihop sig och lungvolymen minskar, vilket leder till att trycket ökar (Boyles lag igen) och luft strömmar ut ur lungorna (från högt tryck till lågt tryck). Du andas sedan in och ut igen, och igen, och upprepar denna cykel enligt Boyles lag resten av ditt liv (figur 7).
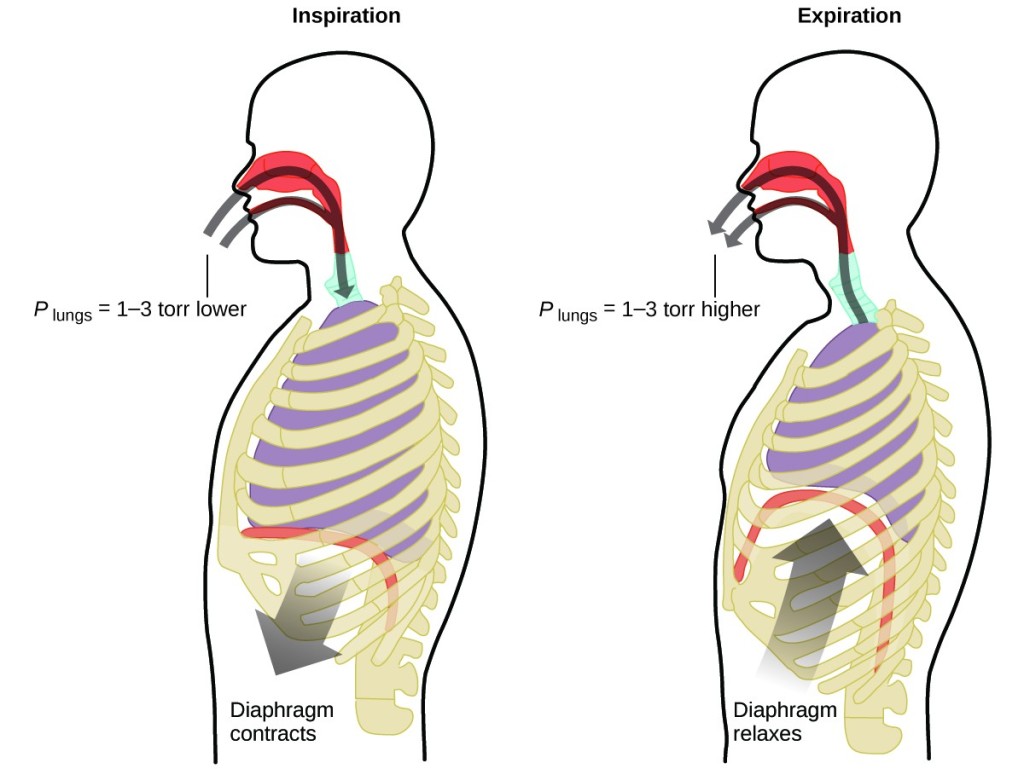
Figur 7. Andningen sker på grund av att expanderande och krympande lungvolym skapar små tryckskillnader mellan dina lungor och din omgivning, vilket gör att luft dras in i och tvingas ut ur lungorna.

Figur 7. Andningen sker på grund av att expanderande och krympande lungvolym skapar små tryckskillnader mellan dina lungor och din omgivning, vilket gör att luft dras in i och tvingas ut ur lungorna.
Mol av gas och volym: Avogadros lag
Den italienska vetenskapsmannen Amedeo Avogadro lade fram en hypotes 1811 för att förklara gasers beteende, där han hävdade att lika stora volymer av alla gaser, uppmätta under samma temperatur- och tryckförhållanden, innehåller lika många molekyler. Med tiden stöddes detta förhållande av många experimentella observationer och uttrycks i Avogadros lag: För en innesluten gas är volymen (V) och antalet mol (n) direkt proportionella om trycket och temperaturen förblir konstanta.
I ekvationsform skrivs detta som:
\large\begin{array}{ccccc}V\propto n& \text{or}& V=k\times n& \text{or}& \frac{{V}_{1}}}{{n}_{1}}}=\frac{{V}_{2}}{{n}_{2}}}\end{array}
Matematiska samband kan också bestämmas för de andra variabelparen, såsom P mot n och n mot T.
Glossar
absolut nollpunkt: temperatur vid vilken volymen av en gas skulle vara noll enligt Charles’ lag.
Avogadros lag: Volymen av en gas vid konstant temperatur och tryck är proportionell mot antalet gasmolekyler
Boyles lag: Volymen av ett givet antal mol gas som hålls vid konstant temperatur är omvänt proportionell mot det tryck under vilket den mäts
Charles lag: Volymen av ett givet antal mol gas är direkt proportionell mot dess kelvin-temperatur när trycket hålls konstant
Gay-Lussacs lag: Volymen av ett givet antal mol gas är direkt proportionell mot dess kelvin-temperatur när trycket hålls konstant
Gay-Lussacs lag: (även Amontons lag) trycket för ett givet antal mol gas är direkt proportionellt mot dess Kelvin-temperatur när volymen hålls konstant