Ett växande område av intresse för forskare som utforskar betydelse, makt eller inflytande mellan entiteter kallas för Grafteori. Grafteorins rötter började 1736 när matematikern Carl Ehler presenterade Leonhard Euler för problemet Bridges of Konigsberg.
Problemet Bridges of Konigsberg har sin grund i den före detta tyska staden Konigsberg som ligger på båda sidor av floden Pregel. I centrum fanns det två stora öar som var förbundna med varandra och med flodbankerna genom sju broar. Carl Ehler blev besatt av att hitta en väg att gå genom var och en av de sju broarna utan att gå över någon av dem mer än en gång. Ehler tog kontakt med Leonhard Euler, en schweizisk matematiker. Euler bekräftade Ehlers hypotes att problemet inte hade någon lösning, och Eulers förklaring informerade om ett nytt matematiskt paradigm som kallades Geometry of Position.
Eulers nya geometriparadigm fastslog att broarnas placering inte spelade någon roll. Problemet kan istället förenklas genom att göra varje bro till en punkt (nod) med linjer (kanter) som representerar länkar mellan dem. Denna praxis att använda noder och kanter är nu känd som grafteori.
Du kan läsa mer om problemet med broarna i Königsberg här.
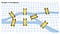
I början tjänade grafteorin inte mycket till problemlösning och var inte särskilt uppskattad av matematikerna. Modern beräkningskraft för att bearbeta stora permutationer har dock gjort Grafteorins principer mer praktiska. I den här artikeln lär du dig att tillämpa grafteorins principer på Pythonbaserad analys.


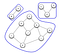
Inte alla nätverk i ett grafsystem är sammankopplade. Det är denna avkoppling som gör att komponenter bildas. Som visas i grafen nedan bildas en komponent endast när varje nod har en väg till andra noder.
Applicerad grafteori i Python
I Python används networkx ofta för tillämpad grafteori även känd som nätverksanalys . Paketet har användbara funktioner för att snabbt sammanfatta egenskaperna hos en graf. Du kan granska stegen nedan och följa med när vi skapar en graf och förstår dess uppbyggnad.
Först skapar koden nedan ett tomt grafobjekt P. I nästa steg läggs noder till och kanter beskrivs.
Argument som <object>.nodes() eller <object>.edges() är snabba sätt att visa alla noder och kanter i grafsystemet.
print(P.nodes())print(P.edges())
Slutligt används nx.draw för att visualisera nätverket.
%matplotlib inline
import matplotlib.pyplot as plt
nx.draw(P, with_labels = True)
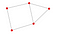
Övningar 1:
Nu när grundläggande begrepp om grafer har diskuterats är följande övningar en bra metod för att öva:
- Hur många noder finns i grafen ovan?
- Hur många kanter finns i grafen ovan?
- Vad är geodetisk för E och C?
- Är det mer än en komponent i grafen?
Användning av riktiga data
Övningen nedan kommer att använda data för flygresor inom Unites States år 2015. Datamängden omfattar ursprungs- och destinationsflygplatser samt attribut som beskriver flygningen, inklusive flygtid och förseningar (väder-, säkerhets- eller flygbolagsrelaterade).
Då datamängden är stor kommer övningen att koncentrera sig på flygningar med ursprung i Los Angeles-området (Los Angeles (LAX), Burbank (BUR), Orange County (SNA) och San Bernardino County (ONT)). Dessutom kommer fokus att ligga på att granska flygningar som liknar mitt reseschema för Deloitte – att flyga ut på söndagar och återvända på torsdagar.
Då vi redan har uppgifter om ursprung och destination kommer ****fields ORIGIN_AIRPORT och DESTINATION_AIRPORT att fungera som källfält för noder och kanter – det finns inget behov av att skapa noder eller kanter som vi gjorde i den första övningen. När noder har definierats kommer <object>.edges() att tillhandahålla alla parvisa relationer mellan dem. Slutligen kommer nx.draw att hjälpa till att skapa en graf för kanterna.

FG.edges()

nx.draw(FG, with_labels = True)

I ovanstående resultat, noderna är märkta med flygplatskoder. Alla kanter leder till en av de fyra flygplatserna i Los Angeles-området eftersom dessa fyra var de enda som valdes ut för denna övning. Los Angeles International (LAX) är den största flygplatsen bland de fyra och grafen visar tydligt att många städer endast kan nås från LAX och inte från andra mindre flygplatser. Detta visar på LAX:s anslutningsgrad, eller graden av centralitet. I networkx används nx.algorithms.degree_centrality(<object>) ****för att hitta centraliteten för varje nod i grafsystemet.
# Calculating the centrality of each of the airports
nx.algorithms.degree_centrality(FG)
Vi kan gå mer granulärt tillväga och använda en kort ”for-slinga” för att ta fram kanter mellan två områden av intresse. Följande kod används till exempel för att hitta alla möjliga flygningar från San Bernardino County (ONT) till Newark (EWR) antingen på söndag eller torsdag.
Amellan de olika flygalternativen mellan San Bernardino County och Newark kan nx.dijkstra_path användas för att hitta den euklidiska banan (eller den kortaste banan).
#Finding the dijkstra path
djk_path = nx.dijkstra_path(FG, source='ONT', target='EWR')
djk_path
Övningar 2:
- Förbered följande graf med hjälp av
nx.draw(). Observera: ditt nätverk kanske inte ser exakt likadant ut, men vägar, kanter och noder bör överensstämma med nätverket nedan. - Utskrift av alla kanter.
- Vad är den kortaste vägen från L till F?

.