Vad är det för mening med teckentabeller?
En bra fråga är nu: vad är det för mening med att lära sig om teckentabeller? Det enkla svaret är att symmetrin och den tillhörande teckentabellen för en molekyl kan användas för att tolka och förutsäga många aspekter av kemiskt betydelsefulla spektroskopier samt bindningar. Vi kommer att illustrera detta härnäst genom att fokusera på en molekyls vibrationella lägen.
I laboratoriet kan vi samla in användbara experimentella data med hjälp av infraröd (IR) och Raman-spektroskopi. Dessa data kan jämföras med antalet IR- och/eller Raman-aktiva band som förutspås genom tillämpning av gruppteori och den korrekta teckentabellen. Matematiken (gruppteori och matrisalgebra) bakom denna behandling tjänar som en solid teoretisk grund. De manipulationer som beskrivs nedan fungerar eftersom alla symmetrioperationer i en molekyl utgör en matematisk grupp och lyder gruppens regler. Som tidigare nämnts behöver vi inte behärska detta matematiska område för att kunna använda teckentabeller på ett bra sätt.
Frihetsgrader och vibrationer i molekyler
Här kommer vi inledningsvis att diskutera frihetsgraderna för en enkel molekyl (vatten). Vi kommer mycket snabbt att se varför det är mycket fördelaktigt att använda symmetri när vi undersöker större molekyler.
För en molekyl med ”N” atomer finns det 3N frihetsgrader (kom ihåg att vi lever i en tredimensionell värld med x-, y- och z-koordinater). För en icke-linjär molekyl kan 3 frihetsgrader betecknas som translationer – rörelse av en kropp som helhet (Tx, Ty, Tz) och 3 som rotationer (Rx, Ry, Rz). De återstående rörelserna hos atomerna är förskjutningar av atomerna från deras medelpositioner – tyngdpunkten ändras inte. Dessa grundläggande vibrationer kallas ”normala lägen”. En icke-linjär molekyl har således 3N-6 normala lägen. För vatten är antalet normala lägen 3 (3 x 3 – 6 = 3). För linjära molekyler finns det 3N-5 normala lägen.
För vatten, som naturligtvis har studerats intensivt, vet vi att de 3 vibrationerna är följande:
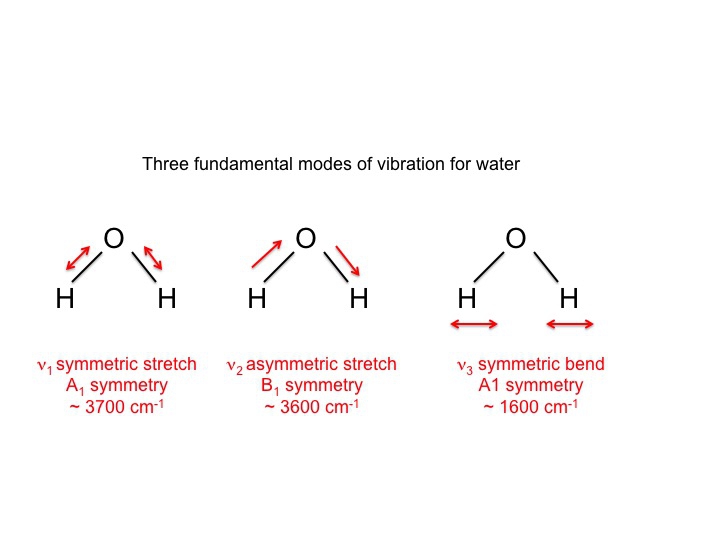
Symbolerna som används för att beskriva dessa lägen (A1, B1) är samma Mulliken-symboler som vi stötte på i diskussionen om teckenbord. Med andra ord kan vibrationerna, som är molekylära egenskaper, beskrivas av symmetriarter eller irreducible representationer. Faktum är att mycket av den litteratur som rör vibrationsspektroskopi använder dessa symboler som ett kortfattat sätt att kommunicera information.
Det borde vara ganska uppenbart att antalet vibrationer ökar snabbt med även blygsamma ökningar av antalet atomer i molekylen. Att bestämma vibrationstyperna genom inspektion (som vi gjorde för vatten) blir nu mycket svårare. Tänk till exempel på följande föreningar:
H2O 3 atomer 3 vibrationer
PH3 4 atomer 6 vibrationer
CO22- 4 atomer 6 vibrationer
XeF4 5 atomer 9 vibrationer
B2H6 8 atomer 18 vibrationer
För diboran (B2H6), som har D2h-symmetri, skulle det vara en skrämmande uppgift att genom inspektion ta reda på arten och symmetriarten för alla 18 vibrationer. Beväpnad med teckentabellen för D2h och kunskap om symmetriegenskaper är uppgiften att bestämma symmetriarten för alla vibrationer dock okomplicerad.
För vatten kan vi presentera teckentabellen (C2v) med de 3 vibrationerna (ν1, v2, v3) listade i kolumnen för molekylära egenskaper enligt nedan. (ν = grekisk symbol ”nu”)

Hursomhelst är detta tillvägagångssätt i allmänhet opraktiskt. Ta pyridin (C5H5N) som exempel. Punktgruppen är också C2v men molekylen har 11 atomer. Antalet fundamentala vibrationslägen är 27 ( 3 x 11 – 6 = 27).
I detta fall skulle vi behöva upprätta en C2v-karaktertabell som visar symmetrierna för alla 27 vibrationer. Av denna anledning tas vibrationer normalt inte med i teckentabeller. Istället är det upp till användaren (du) att bestämma antalet och typen av vibrationer (enligt definitionen av deras symmetriarter) för alla molekyler som man stöter på. Hur vi gör detta beskrivs nedan.
Reducible Representations
Som tidigare nämnts är en av de viktiga egenskaperna hos teckentabeller att symmetrioperationerna ingår i en matematisk grupp och att viktiga relationer finns mellan dem. I allmänhet kan samma sak sägas om symmetriarter eller irreducible representationer av molekylära egenskaper. Produkterna från kombinationen av tecken av irreducerbara representationer antingen genom multiplikation eller addition/subtraktion följer också gruppens regler. De nya representationerna är inte längre de enklaste möjliga och kallas ”reducerbara representationer” eftersom de kan ”reduceras” ner till sina beståndsdelar.
För vatten till exempel kan symmetrierna för översättningarna (Tx, Ty, Tz) hämtas direkt från C2v-teckentabellen. De är A1, B1 och B2. Vi kan representera alla dessa tre frihetsgrader med en representation ΓT och vi kan skriva uttrycket nedan. (Γ = stor grekisk bokstav ”gamma”).
ΓT = A1 + B1 + B2
Vi vet att A1, B1 och B2 bara är förkortningar för symmetriarter (irreducible representationer). Vi kan därför helt enkelt skriva ner tecknen för ΓT genom att addera de enskilda tecknen för A1, B1 och B2 från C2v-teckentabellen.
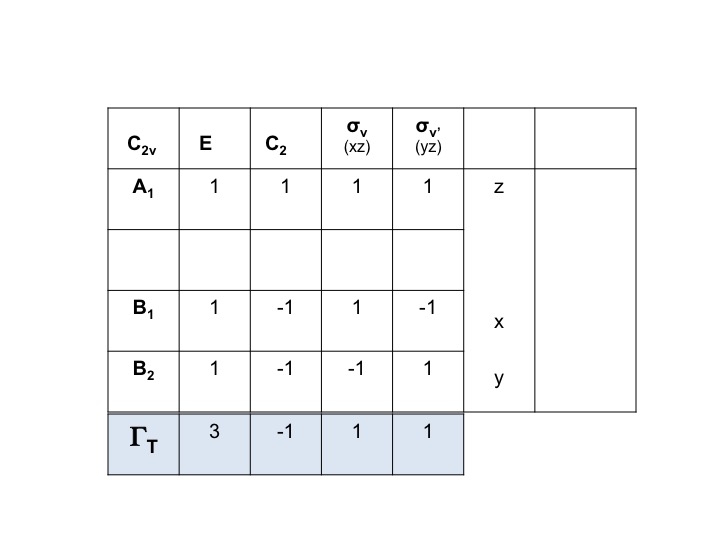
Thos ΓT = 3 -1 1 1.
Detta är en giltig reducerbar representation och en medlem av C2v-gruppen.
På liknande sätt kan vi skriva ner den reducerbara representationen för alla tre rotationer och alla vibrationer.
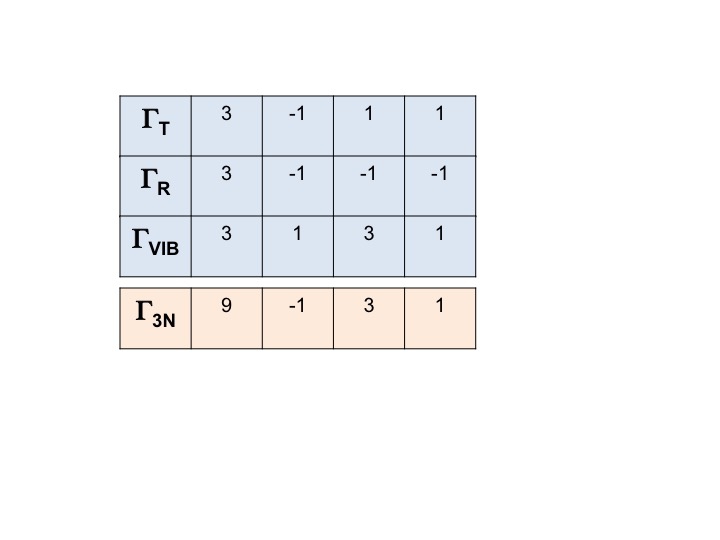
Den representationen för ALLA frihetsgrader för molekylen (3N) kan skrivas som
Γ3N = ΓT + ΓR + ΓVIB
och den reducerbara representationen för den erhålls genom att helt enkelt summera tecknen för ΓT, ΓR och ΓVIB.
Γ3N = 9 -1 3 1
Notera detta – det kommer att dyka upp senare!
Och även om teckenuppsättningen 9 -1 3 1 är en giltig medlem av C2v-gruppen är den inte särskilt användbar när man diskuterar molekylära egenskaper. Vad som verkligen behövs är språket för de kortfattade symmetriarterna (Mulliken-symboler, A1, B1 etc.). Med andra ord vill vi uttrycka Γ3N i termer av A1, B1 osv. Från den information som behandlats ovan kan det lätt visas genom inspektion att:
Γ3N = 3A1 +A2 + 3B1 +2B2
Den goda nyheten är att för andra mer komplexa molekyler behöver vi inte utföra denna uppgift genom inspektion eftersom:
1. Vi kan enkelt generera Γ3N som en reducerbar representation för en molekyl (om vi känner till dess punktgruppsymmetri).
2. Vi kan enkelt omvandla den reducerbara representationen Γ3N till summan av dess symmetriarter (Mulliken-symboler) med hjälp av en ”enkel” formel som kallas reduktionsformeln.
Generell metod för att erhålla Γ3N
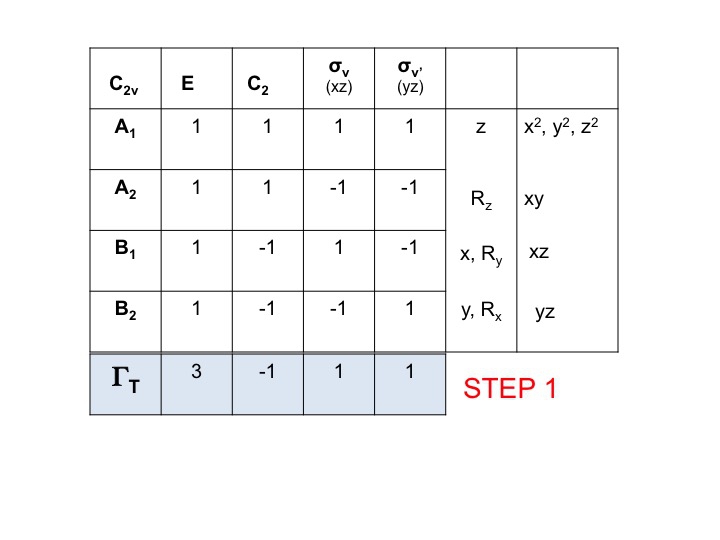
Steg 1
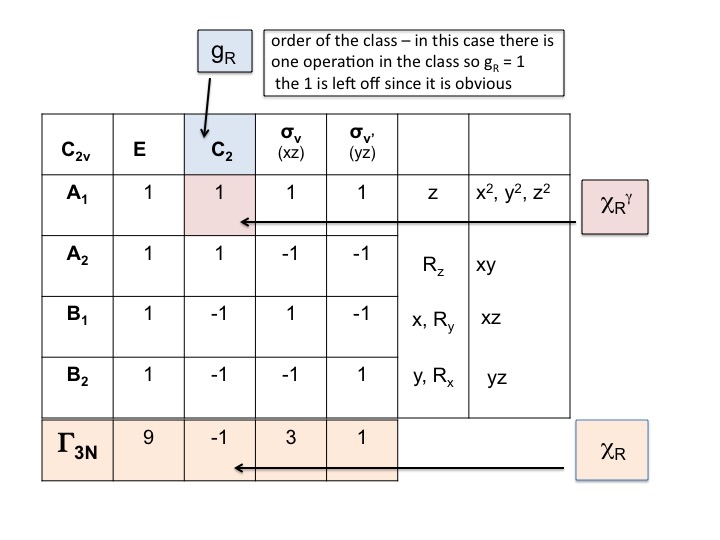
Tag teckentabellen för molekylen och lägg till en rad längst ner. I denna rad genererar du den reducerbara representationen för ΓT (eller Γxyz) som vi gjorde ovan, helt enkelt genom att lägga till de tecken för varje operation som motsvarar molekylens egenskaper för x, y och z. För C2v har vi redan visat att dessa är de tecken som motsvarar A1, B1 och B2.
Steg 2
Tillägg ytterligare en rad under ΓT och skriv ner antalet atomer som INTE ÄNDRAR sin plats under varje symmetrioperation. Det är här du inser hur användbar en riktig molekylmodelluppsättning är. För att göra detta måste du också veta var symmetrielementen finns och hur symmetrioperationerna påverkar molekylen. Naturligtvis vet du redan hur man gör detta eftersom du har studerat Schönflies notation och vet hur man tilldelar en molekyls punktgrupp. Karaktärstabellen har också alla symmetrioperationer listade efter klass längs den översta raden.
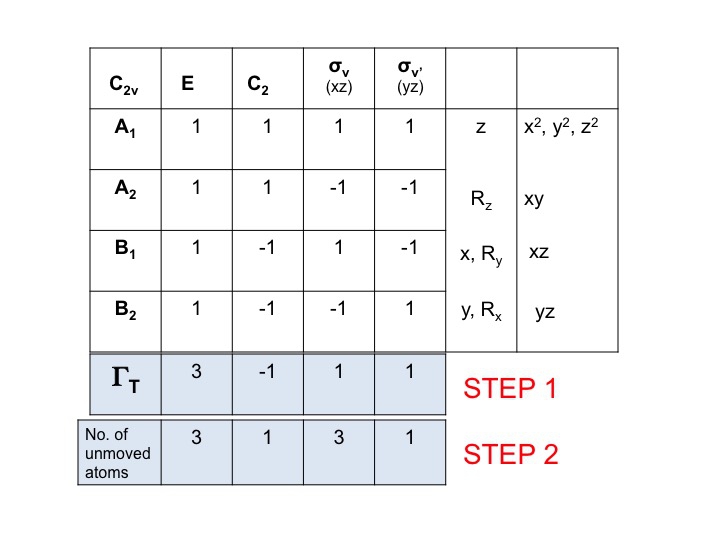
Så för vatten (3 atomer) under E finns det 3 orörliga atomer, men för C2 rör sig båda H-atomerna men eftersom O-atomen sitter på C2-axeln ändrar den inte sin plats och därför noterar vi 1 under C2-kolumnen. Den nya uppsättning tal som genererades i steg 2 (3 1 3 3 1) är också en reducerbar representation i C2v och lyder gruppens regler.
Steg 3
I detta steg multiplicerar vi helt enkelt ihop de tecken som har genererats i steg 1 och 2. Resultatet (tredje raden) är den reducerbara representationen för Γ3N (eller ΓTOT). Så enkelt är det.
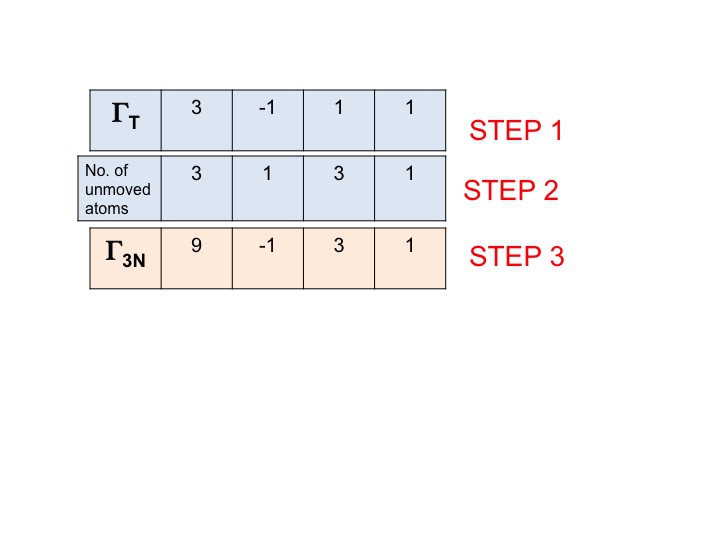
Du kommer att notera att den nya reducerbara representationen (9 -1 1 3) är identisk med representationen för Γ3N som vi tidigare fick fram genom inspektion.
Reduktion av den reducerbara representationen
För att omvandla EN reducerbar representation till summan av dess irreducerbara representationer (symmetriarter eller Mulliken-symboler) använder vi en reduktionsformel:

Den här informationen kan du enkelt hitta i teckentabellen:
Tillbaka till vårt exempel för vatten: Punktgrupp C2v, ordning (g) = 4
Den reducerbara representationen för Γ3N = 9 -1 3 1
Antalet gånger A1 förekommer i denna representation är därför
aA1 = 1/4 { 1.1.9 + 1.1.1. (-1) + 1.1.3 +1.1.1} = 3
så Γ3N innehåller 3 arter med A1-symmetri. Antalet övriga symmetriarter beräknas på följande sätt:
aA2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1).3 + 1.(-1).1 } = 1 en A2 närvarande
aB1 = 1/4 { 1.1.9 + 1.(-1).(-1) + 1.1.3 + 1.(-1).1} = 3 3 B1 närvarande
aB2 = 1/4 {1.1.9 + 1.(-1)(-1) + 1.(-1).3 + 1.1.1.1} = 2 2 B2 närvarande
Vi kan nu skriva Γ3N = 3A1 + A2 + 3B1 + 2B2 (exakt vad vi fick genom ”inspektion” ovan. Vi kan nu subtrahera symmetriarterna för translationer och rotationer och detta ger oss antalet och symmetriarterna för de fundamentala vibrationslägena. ΓT och ΓR kan fås direkt från karaktärstabellen.
Γ3N = 3A1 + A2 + 3B1 + 2B2
ΓT = A1 + B1 + B2
ΓR = A2 + B1 + B2
ΓVIB = Γ3N – ΓT – ΓR = 2A1 +B1
Så de tre normala vibrationerna för vatten har symmetrierna A1, A1 och B1.
Vi har nu en allmän metod för att bestämma alla grundläggande vibrationslägen för en molekyl och uttrycka dessa lägen i Mulliken-symbolernas kortfattade språk. Detta är en av de övningar som du kommer att testas på i tentamen 1. Det bästa sättet att bli säker på den här metoden är att öva på så många möjliga exempel som möjligt!
Nästa: Urvalsregler