Inledning

En av de vanligaste användningarna av TensorFlow och Keras är igenkänning/klassificering av bilder. Om du vill lära dig hur du använder Keras för att klassificera eller känna igen bilder kommer den här artikeln att lära dig hur.

Definitioner

Om du inte är klar över de grundläggande begreppen bakom bildigenkänning kommer det att vara svårt att helt förstå resten av den här artikeln. Så innan vi går vidare tar vi oss en stund för att definiera några termer.

TensorFlow/Keras

Credit: commons.wikimedia.org

TensorFlow är ett bibliotek med öppen källkod som skapats för Python av Google Brain-teamet. TensorFlow sammanställer många olika algoritmer och modeller tillsammans, vilket gör det möjligt för användaren att implementera djupa neurala nätverk för användning i uppgifter som bildigenkänning/klassificering och behandling av naturliga språk. TensorFlow är ett kraftfullt ramverk som fungerar genom att implementera en serie bearbetningsnoder, där varje nod representerar en matematisk operation, och där hela serien av noder kallas för en ”graf”.

Inom Keras är det ett API (gränssnitt för tillämpningsprogrammering) på hög nivå som kan använda TensorFlows funktioner underifrån (liksom andra ML-bibliotek som Theano). Keras utformades med användarvänlighet och modularitet som ledstjärnor. I praktiken gör Keras det så enkelt som möjligt att implementera de många kraftfulla men ofta komplexa funktionerna i TensorFlow, och det är konfigurerat för att fungera med Python utan några större ändringar eller konfigurationer.

Bildigenkänning (klassificering)

Bildigenkänning hänvisar till uppgiften att mata in en bild i ett neuralt nätverk och få det att ge ut någon form av etikett för den bilden. Den etikett som nätverket ger ut kommer att motsvara en fördefinierad klass. Det kan finnas flera klasser som bilden kan märkas som, eller bara en. Om det finns en enda klass används ofta termen ”igenkänning”, medan en igenkänningsuppgift med flera klasser ofta kallas ”klassificering”.

En delmängd av bildklassificering är objektsökning, där specifika exempel på objekt identifieras som tillhörande en viss klass, t.ex. djur, bilar eller människor.

Funktionsextrahering

För att kunna utföra bildigenkänning/klassificering måste det neurala nätverket utföra funktionsextraktion. Funktioner är de delar av data som du bryr dig om och som kommer att matas genom nätverket. I det specifika fallet med bildigenkänning är funktionerna grupper av pixlar, som kanter och punkter, i ett objekt som nätverket kommer att analysera efter mönster.

Funktioner för bildigenkänning (eller funktionsextraktion) är processen för att dra ut de relevanta funktionerna ur en inmatad bild så att dessa funktioner kan analyseras. Många bilder innehåller kommentarer eller metadata om bilden som hjälper nätverket att hitta de relevanta funktionerna.

Hur neurala nätverk lär sig att känna igen bilder

Att få en uppfattning om hur ett neuralt nätverk känner igen bilder kommer att hjälpa dig när du implementerar en modell för ett neuralt nätverk, så låt oss kort utforska processen för bildigenkänning i de kommande avsnitten.

Feature Extraction With Filters

Credit: commons.wikimedia.org

Det första lagret i ett neuralt nätverk tar in alla pixlar i en bild. När alla data har matats in i nätverket appliceras olika filter på bilden, vilket bildar representationer av olika delar av bilden. Detta är feature extraction och skapar ”feature maps”.

Denna process för att extrahera funktioner från en bild utförs med ett ”konvolutionellt lager”, och konvolution är helt enkelt att bilda en representation av en del av en bild. Det är från detta konvolutionskoncept som vi får termen Convolutional Neural Network (CNN), den typ av neuralt nätverk som oftast används vid bildklassificering/igenkänning.

Om du vill visualisera hur det går till att skapa funktionskartor kan du tänka på att lysa med en ficklampa över en bild i ett mörkt rum. När du för strålen över bilden lär du dig om bildens egenskaper. Ett filter är det som nätverket använder för att bilda en representation av bilden, och i den här metaforen är ljuset från ficklampan filtret.

Bredden på din ficklampas stråle styr hur mycket av bilden du undersöker på en gång, och neurala nätverk har en liknande parameter, filterstorleken. Filterstorleken påverkar hur stor del av bilden, hur många pixlar, som undersöks på en gång. En vanlig filterstorlek som används i CNN är 3, och detta täcker både höjd och bredd, så filtret undersöker ett 3 x 3 område av pixlar.

Credit: commons.wikimedia.org

Men även om filterstorleken täcker filtrets höjd och bredd måste filtrets djup också anges.

Hur har en 2D-bild djup?

Digitala bilder återges som höjd, bredd och något RGB-värde som definierar pixelns färger, så det ”djup” som spåras är antalet färgkanaler som bilden har. Gråskala (icke-färg) bilder har endast 1 färgkanal medan färgbilder har 3 djupkanaler.

Allt detta innebär att för ett filter av storlek 3 som appliceras på en helfärgsbild kommer filtrets dimensioner att vara 3 x 3 x 3 x 3. För varje pixel som täcks av filtret multiplicerar nätverket filtervärdena med värdena i själva pixlarna för att få en numerisk representation av den pixeln. Denna process görs sedan för hela bilden för att få en fullständig representation. Filtret flyttas över resten av bilden enligt en parameter som kallas ”stride”, som definierar hur många pixlar filtret ska flyttas med efter att det har beräknat värdet i sin nuvarande position. En konventionell stride-storlek för en CNN är 2.

Slutresultatet av alla dessa beräkningar är en feature map. Den här processen görs vanligtvis med mer än ett filter, vilket bidrar till att bevara bildens komplexitet.

Aktiveringsfunktioner

När funktionskartan för bilden har skapats skickas värdena som representerar bilden genom en aktiveringsfunktion eller ett aktiveringslager. Aktiveringsfunktionen tar värden som representerar bilden, som är i linjär form (dvs. bara en lista med siffror) tack vare det konvolutionella lagret, och ökar deras icke-linjäritet eftersom bilder i sig själva är icke-linjära.

Den typiska aktiveringsfunktionen som används för att åstadkomma detta är en Rectified Linear Unit (ReLU), även om det finns några andra aktiveringsfunktioner som ibland används (du kan läsa om dem här).

Pooling Layers

När uppgifterna har aktiverats skickas de genom ett poolinglager. Pooling ”downsamplar” en bild, vilket innebär att den tar den information som representerar bilden och komprimerar den, vilket gör den mindre. Poolingprocessen gör nätverket mer flexibelt och skickligare på att känna igen objekt/bilder utifrån de relevanta funktionerna.

När vi tittar på en bild är vi vanligtvis inte intresserade av all information i bakgrunden av bilden, utan bara av de funktioner som vi bryr oss om, t.ex. människor eller djur.

På samma sätt kommer ett poolinglager i ett CNN att abstrahera bort de onödiga delarna av bilden och endast behålla de delar av bilden som det anser vara relevanta, vilket styrs av den specificerade storleken på poolinglagret.

Då det måste fatta beslut om de mest relevanta delarna av bilden är förhoppningen att nätverket endast ska lära sig de delar av bilden som verkligen representerar objektet i fråga. Detta hjälper till att förhindra överanpassning, där nätverket lär sig aspekter av träningsfallet för bra och misslyckas med att generalisera till nya data.

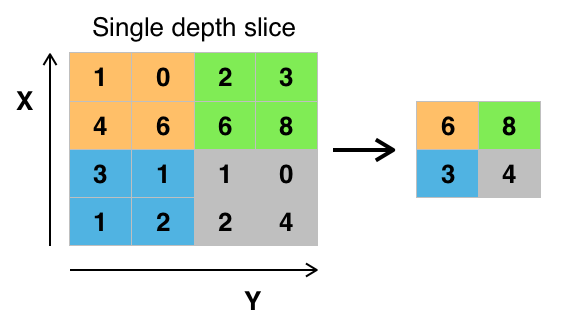
Credit: commons.wikimedia.org

Det finns olika sätt att sammanföra värden, men max pooling är det vanligaste sättet. Max pooling erhåller det maximala värdet för pixlarna inom ett enda filter (inom en enda punkt i bilden). Detta ger 3/4-delar av informationen, om man antar att 2 x 2 filter används.

De maximala värdena för pixlarna används för att ta hänsyn till eventuella bildförvrängningar, och parametrarna/storleken på bilden minskas för att kontrollera överanpassning. Det finns andra typer av poolning, t.ex. genomsnittlig poolning eller summapoolning, men dessa används inte lika ofta eftersom maxpoolning tenderar att ge bättre noggrannhet.

Flattening

De sista lagren i vår CNN, de tätt sammankopplade lagren, kräver att data är i form av en vektor för att kunna bearbetas. Av denna anledning måste uppgifterna ”plattas”. Värdena komprimeras till en lång vektor eller en kolumn med sekventiellt ordnade tal.

Fullt sammankopplade lager

De sista lagren i CNN är tätt sammankopplade lager, eller ett artificiellt neuralt nätverk (ANN). ANN:s primära funktion är att analysera de ingående funktionerna och kombinera dem till olika attribut som hjälper till med klassificeringen. Dessa lager bildar i huvudsak samlingar av neuroner som representerar olika delar av objektet i fråga, och en samling neuroner kan representera en hunds slappa öron eller ett äppels rödhet. När tillräckligt många av dessa neuroner aktiveras som svar på en inmatningsbild kommer bilden att klassificeras som ett objekt.

Credit: commons.wikimedia.org

Felet, eller skillnaden mellan de beräknade värdena och det förväntade värdet i träningsuppsättningen, beräknas av ANN. Nätverket genomgår sedan backpropagation, där en viss neurons inflytande på en neuron i nästa lager beräknas och dess inflytande justeras. Detta görs för att optimera modellens prestanda. Denna process upprepas sedan om och om igen. Detta är hur nätverket tränar på data och lär sig associationer mellan inmatningsfunktioner och utgångsklasser.

Neuronerna i de mellersta fullt anslutna lagren kommer att ge ut binära värden som relaterar till de möjliga klasserna. Om du har fyra olika klasser (låt oss säga en hund, en bil, ett hus och en person) kommer neuronen att ha ett ”1”-värde för den klass som den tror att bilden representerar och ett ”0”-värde för de andra klasserna.

Det sista fullt sammankopplade lagret kommer att ta emot utdata från lagret före det och leverera en sannolikhet för var och en av klasserna, som summeras till ett. Om det finns ett värde på 0,75 i kategorin ”hund” representerar det en 75-procentig säkerhet att bilden är en hund.

Bildklassificatorn har nu tränats och bilderna kan skickas in i CNN, som nu kommer att ge ut en gissning om innehållet i bilden.

Arbetsflödet för maskininlärning

Innan vi hoppar in i ett exempel på hur man tränar en bildklassificator, ska vi ta ett ögonblick för att förstå arbetsflödet eller pipelinen för maskininlärning. Processen för att träna en modell av ett neuralt nätverk är ganska standardiserad och kan delas upp i fyra olika faser.

Dataförberedelse

Först måste du samla in dina data och lägga dem i en form som nätverket kan träna på. Detta innebär att samla in bilder och märka dem. Även om du har laddat ner en datamängd som någon annan har förberett finns det sannolikt en förbehandling eller förberedelse som du måste göra innan du kan använda den för träning. Förberedelse av data är en konst i sig. Det handlar om att hantera saker som saknade värden, skadade data, data i fel format, felaktiga etiketter etc.

I den här artikeln kommer vi att använda ett förbehandlat dataset.

Skapande av modellen

Skapandet av modellen för det neurala nätverket innebär att man måste göra val om olika parametrar och hyperparametrar. Du måste fatta beslut om hur många lager som ska användas i din modell, hur stora ingångar och utgångar lagren ska ha, vilken typ av aktiveringsfunktioner du ska använda, om du ska använda dropout eller inte osv.

Att lära sig vilka parametrar och hyperparametrar som ska användas kommer med tiden (och en hel del studier), men redan från början finns det några heuristiker som du kan använda för att komma igång och vi kommer att ta upp några av dessa under implementeringsexemplet.

Träning av modellen

När du har skapat din modell skapar du helt enkelt en instans av modellen och anpassar den med dina träningsdata. Det största övervägandet när du tränar en modell är hur lång tid det tar att träna modellen. Du kan ange längden på träningen för ett nätverk genom att ange antalet epoker att träna över. Ju längre du tränar en modell, desto mer kommer dess prestanda att förbättras, men för många träningsepoker och du riskerar att överanpassa.

Att välja antalet epoker att träna under är något som du får en känsla för, och det är vanligt att spara vikterna i ett nätverk mellan träningspassen så att du inte behöver börja om från början när du väl har gjort vissa framsteg med att träna nätverket.

Modellutvärdering

Det finns flera steg för att utvärdera modellen. Det första steget i utvärderingen av modellen är att jämföra modellens prestanda mot en valideringsdatamängd, en datamängd som modellen inte har tränats på. Du kommer att jämföra modellens prestanda mot denna valideringsuppsättning och analysera dess prestanda med hjälp av olika mått.

Det finns olika mått för att bestämma prestandan hos en modell för neurala nätverk, men det vanligaste måttet är ”noggrannhet”, antalet korrekt klassificerade bilder dividerat med det totala antalet bilder i din datauppsättning.

När du har sett modellens noggrannhet på en valideringsdatamängd går du vanligtvis tillbaka och tränar nätverket igen med något justerade parametrar, eftersom det är osannolikt att du blir nöjd med nätverkets prestanda första gången du tränar. Du fortsätter att justera parametrarna för ditt nätverk, träna om det och mäta dess prestanda tills du är nöjd med nätverkets noggrannhet.

Slutligen testar du nätverkets prestanda på en testuppsättning. Denna testuppsättning är en annan uppsättning data som din modell aldrig har sett förut.

Kanske undrar du:

Varför bry sig om testuppsättningen? Om du får en uppfattning om modellens noggrannhet, är inte det syftet med valideringsuppsättningen?

Det är en bra idé att behålla en uppsättning data som nätverket aldrig har sett för testning, eftersom alla justeringar av parametrarna som du gör, i kombination med omtestning av valideringsuppsättningen, kan innebära att ditt nätverk har lärt sig några egenheter hos valideringsuppsättningen som inte kommer att generaliseras till data som inte ingår i urvalet.

Syftet med testuppsättningen är därför att kontrollera problem som överanpassning och vara mer säker på att din modell verkligen är anpassad för att fungera i den verkliga världen.

Bildigenkänning med CNN

Vi har behandlat mycket hittills, och om all denna information har varit lite överväldigande bör det göra begreppen mer konkreta att se dem sammanföras i ett exempel på en klassificerare som tränats på en datamängd. Så låt oss titta på ett fullständigt exempel på bildigenkänning med Keras, från laddning av data till utvärdering.

Credit: www.cs.toronto.edu

För att börja behöver vi ett dataset att träna på. I det här exemplet kommer vi att använda det berömda datasetet CIFAR-10. CIFAR-10 är ett stort bilddataset som innehåller över 60 000 bilder som representerar 10 olika klasser av objekt som katter, flygplan och bilar.

Bilderna är RGB-färg i fullfärg, men de är ganska små, endast 32 x 32. En bra sak med CIFAR-10-dataset är att det levereras färdigpaketerat med Keras, så det är mycket enkelt att ladda datasetetet och bilderna behöver mycket lite förbehandling.

Det första vi bör göra är att importera de nödvändiga biblioteken. Jag kommer att visa hur dessa importer används allteftersom, men för tillfället vet du att vi kommer att använda oss av Numpy och olika moduler som är kopplade till Keras:

import numpyfrom keras.models import Sequentialfrom keras.layers import Dense, Dropout, Flatten, BatchNormalization, Activationfrom keras.layers.convolutional import Conv2D, MaxPooling2Dfrom keras.constraints import maxnormfrom keras.utils import np_utils

Vi kommer att använda oss av ett slumpmässigt frö här så att de resultat som uppnås i den här artikeln kan replikeras av dig, vilket är anledningen till att vi behöver numpy:

# Set random seed for purposes of reproducibilityseed = 21

Förberedelser för data

Vi behöver ytterligare en import: datasetetet.

from keras.datasets import cifar10

Nu ska vi ladda in datasetet. Det kan vi göra helt enkelt genom att ange vilka variabler vi vill ladda in data i och sedan använda funktionen load_data():

# loading in the data (X_train, y_train), (X_test, y_test) = cifar10.load_data()

I de flesta fall måste du göra en viss förbehandling av dina data för att få dem redo att användas, men eftersom vi använder en förpaketerad dataset behöver mycket lite förbehandling göras. En sak vi vill göra är att normalisera indata.

Om värdena i indata ligger inom ett för stort intervall kan det ha en negativ inverkan på hur nätverket presterar. I det här fallet är ingångsvärdena pixlarna i bilden, som har ett värde mellan 0 och 255.

För att normalisera data kan vi alltså helt enkelt dividera bildvärdena med 255. För att göra detta måste vi först göra data till en floattyp, eftersom de för närvarande är heltal. Vi kan göra detta genom att använda kommandot astype() Numpy och sedan deklarera vilken datatyp vi vill ha:

# normalize the inputs from 0-255 to between 0 and 1 by dividing by 255 X_train = X_train.astype('float32')X_test = X_test.astype('float32')X_train = X_train / 255.0X_test = X_test / 255.0

En annan sak som vi måste göra för att göra data redo för nätverket är att one-hot-koda värdena. Jag kommer inte att gå in på detaljerna kring one-hot-kodning här, men för tillfället ska du veta att bilderna inte kan användas av nätverket som de är, de måste kodas först och one-hot-kodning används bäst när man gör binär klassificering.

Vi gör i praktiken binär klassificering här eftersom en bild antingen tillhör en klass eller inte, den kan inte hamna någonstans däremellan. Numpy-kommandot to_categorical() används för en snabbkodning. Det är därför vi importerade funktionen np_utils från Keras, eftersom den innehåller to_categorical().

Vi måste också ange antalet klasser som finns i datasetet, så att vi vet hur många neuroner vi ska komprimera det sista lagret ner till:

# one hot encode outputsy_train = np_utils.to_categorical(y_train)y_test = np_utils.to_categorical(y_test)class_num = y_test.shape

Design av modellen

Vi har kommit fram till det stadium där vi designar CNN-modellen. Det första vi måste göra är att definiera vilket format vi vill använda för modellen, Keras har flera olika format eller ritningar för att bygga modeller på, men Sequential är det vanligaste och därför har vi importerat det från Keras.

Skapa modellen

model = Sequential()

Det första lagret i vår modell är ett konvolutionellt lager. Det kommer att ta emot inmatningarna och köra konvolutionella filter på dem.

När vi implementerar dessa i Keras måste vi ange antalet kanaler/filter vi vill ha (det är de 32 nedan), storleken på filtret vi vill ha (3 x 3 i det här fallet), formen på inmatningen (när vi skapar det första lagret) och den aktivering och utfyllnad vi behöver.

Som nämnts är relu den vanligaste aktiveringen, och padding='same' betyder bara att vi inte ändrar storleken på bilden alls:

model.add(Conv2D(32, (3, 3), input_shape=X_train.shape, padding='same'))model.add(Activation('relu'))

Notera: Du kan också rada upp aktiveringarna och poolningarna tillsammans, så här:

model.add(Conv2D(32, (3, 3), input_shape=(3, 32, 32), activation='relu', padding='same'))

Nu kommer vi att göra ett dropout-lager för att förhindra överanpassning, vilket fungerar genom att slumpmässigt eliminera några av kopplingarna mellan lagren (0.2 innebär att den slopar 20 % av de befintliga förbindelserna):

model.add(Dropout(0.2))

Vi kanske också vill göra en normalisering av partierna här. Batch Normalization normaliserar ingångarna på väg in i nästa lager, vilket säkerställer att nätverket alltid skapar aktiveringar med samma fördelning som vi önskar:

model.add(BatchNormalization())

Nu kommer ytterligare ett konvolutionellt lager, men filterstorleken ökar så att nätverket kan lära sig mer komplexa representationer:

model.add(Conv2D(64, (3, 3), padding='same'))model.add(Activation('relu'))

Här kommer poolinglagret, som vi diskuterat tidigare hjälper det här till att göra bildklassificatorn mer robust så att den kan lära sig relevanta mönster. Där finns också bortfallet och normaliseringen av partierna:

model.add(MaxPooling2D(pool_size=(2, 2)))model.add(Dropout(0.2))model.add(BatchNormalization())

Detta är det grundläggande flödet för den första halvan av en CNN-implementering: Konvolutionär, aktivering, bortfall, pooling. Du kan nu se varför vi har importerat Dropout, BatchNormalization, Activation, Conv2d och MaxPooling2d.

Du kan variera det exakta antalet konvolutionella lager som du har efter eget tycke, även om varje lager ger mer beräkningskostnader. Observera att när du lägger till konvolutionella lager ökar du vanligtvis deras antal filter så att modellen kan lära sig mer komplexa representationer. Om de antal som valts för dessa lager verkar något godtyckligt är det bara att veta att du i allmänhet ökar antalet filter allteftersom du fortsätter och att det rekommenderas att göra dem till potenser av 2, vilket kan ge en liten fördel när du tränar på en GPU.

Det är viktigt att inte ha för många poolningslager, eftersom varje poolning kastar bort en del data. Om du poolar för ofta kommer det att leda till att det nästan inte finns något för de tätt sammankopplade lagren att lära sig om när data når dem.

Det exakta antalet poolningslager som du bör använda kommer att variera beroende på vilken uppgift du utför, och det är något som du kommer att få en känsla för med tiden. Eftersom bilderna är så små här redan kommer vi inte att poola mer än två gånger.

Du kan nu upprepa dessa lager för att ge ditt nätverk fler representationer att arbeta utifrån:

model.add(Conv2D(64, (3, 3), padding='same'))model.add(Activation('relu'))model.add(MaxPooling2D(pool_size=(2, 2)))model.add(Dropout(0.2))model.add(BatchNormalization()) model.add(Conv2D(128, (3, 3), padding='same'))model.add(Activation('relu'))model.add(Dropout(0.2))model.add(BatchNormalization())

När vi är färdiga med de konvolutionella lagren behöver vi Flatten data, vilket är anledningen till att vi importerade funktionen ovan. Vi lägger också till ett lager med bortfall igen:

model.add(Flatten())model.add(Dropout(0.2))

Nu utnyttjar vi Dense importen och skapar det första tätt sammankopplade lagret. Vi måste ange antalet neuroner i det täta lagret. Observera att antalet neuroner i efterföljande lager minskar och slutligen närmar sig samma antal neuroner som det finns klasser i datasetet (i det här fallet 10). Kärnbegränsningen kan reglera data när den lär sig, vilket är ytterligare en sak som hjälper till att förhindra överanpassning. Det är därför vi importerade maxnorm tidigare.

model.add(Dense(256, kernel_constraint=maxnorm(3)))model.add(Activation('relu'))model.add(Dropout(0.2))model.add(BatchNormalization()) model.add(Dense(128, kernel_constraint=maxnorm(3)))model.add(Activation('relu'))model.add(Dropout(0.2))model.add(BatchNormalization())

I det här sista lagret skickar vi in antalet klasser för antalet neuroner. Varje neuron representerar en klass, och utgången från det här lagret blir en vektor med 10 neuroner där varje neuron lagrar en viss sannolikhet för att bilden i fråga tillhör den klass den representerar.

Slutligt väljer aktiveringsfunktionen softmax neuronen med den högsta sannolikheten som utgång, vilket röstar för att bilden tillhör den klassen:

model.add(Dense(class_num))model.add(Activation('softmax'))

Nu när vi har utformat den modell vi vill använda, behöver vi bara kompilera den. Låt oss ange antalet epoker vi vill träna för, samt vilken optimerare vi vill använda.

Optimeraren är det som kommer att ställa in vikterna i ditt nätverk för att närma sig den punkt där förlusten är lägst. Algoritmen Adam är en av de vanligaste optimerarna eftersom den ger bra prestanda på de flesta problem:

epochs = 25optimizer = 'adam'

Låt oss nu kompilera modellen med våra valda parametrar. Låt oss också ange en metrik som ska användas.

model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=)

Vi kan skriva ut modellsammanfattningen för att se hur hela modellen ser ut.

print(model.summary())

Att skriva ut sammanfattningen ger oss en hel del information:

Results: Layer (type) Output Shape Param #=================================================================conv2d_1 (Conv2D) (None, 32, 32, 32) 896_________________________________________________________________activation_1 (Activation) (None, 32, 32, 32) 0_________________________________________________________________dropout_1 (Dropout) (None, 32, 32, 32) 0_________________________________________________________________batch_normalization_1 (Batch (None, 32, 32, 32) 128_________________________________________________________________conv2d_2 (Conv2D) (None, 32, 32, 64) 18496_________________________________________________________________activation_2 (Activation) (None, 32, 32, 64) 0_________________________________________________________________max_pooling2d_1 (MaxPooling2 (None, 16, 16, 64) 0_________________________________________________________________dropout_2 (Dropout) (None, 16, 16, 64) 0_________________________________________________________________batch_normalization_2 (Batch (None, 16, 16, 64) 256_________________________________________________________________conv2d_3 (Conv2D) (None, 16, 16, 64) 36928_________________________________________________________________activation_3 (Activation) (None, 16, 16, 64) 0_________________________________________________________________max_pooling2d_2 (MaxPooling2 (None, 8, 8, 64) 0_________________________________________________________________dropout_3 (Dropout) (None, 8, 8, 64) 0_________________________________________________________________batch_normalization_3 (Batch (None, 8, 8, 64) 256_________________________________________________________________conv2d_4 (Conv2D) (None, 8, 8, 128) 73856_________________________________________________________________activation_4 (Activation) (None, 8, 8, 128) 0_________________________________________________________________dropout_4 (Dropout) (None, 8, 8, 128) 0_________________________________________________________________batch_normalization_4 (Batch (None, 8, 8, 128) 512_________________________________________________________________flatten_1 (Flatten) (None, 8192) 0_________________________________________________________________dropout_5 (Dropout) (None, 8192) 0_________________________________________________________________dense_1 (Dense) (None, 256) 2097408_________________________________________________________________activation_5 (Activation) (None, 256) 0_________________________________________________________________dropout_6 (Dropout) (None, 256) 0_________________________________________________________________batch_normalization_5 (Batch (None, 256) 1024_________________________________________________________________dense_2 (Dense) (None, 128) 32896_________________________________________________________________activation_6 (Activation) (None, 128) 0_________________________________________________________________dropout_7 (Dropout) (None, 128) 0_________________________________________________________________batch_normalization_6 (Batch (None, 128) 512_________________________________________________________________dense_3 (Dense) (None, 10) 1290_________________________________________________________________activation_7 (Activation) (None, 10) 0=================================================================Total params: 2,264,458Trainable params: 2,263,114Non-trainable params: 1,344

Nu kommer vi till att träna modellen. För att göra detta behöver vi bara anropa fit()-funktionen på modellen och skicka in de valda parametrarna.

Här använder jag det frö som jag valde, för reproducerbarhetens skull.

numpy.random.seed(seed)model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=epochs, batch_size=64)

Vi kommer att träna på 50000 prover och validera på 10000 prover.

Körning av den här koden ger:

Epoch 1/2564/50000 - ETA: 16:57 - loss: 3.1479 - acc: 0.0938128/50000 - ETA: 10:12 - loss: 3.0212 - acc: 0.0938192/50000 - ETA: 7:57 - loss: 2.9781 - acc: 0.1250256/50000 - ETA: 6:48 - loss: 2.8830 - acc: 0.1484320/50000 - ETA: 6:07 - loss: 2.8878 - acc: 0.1469384/50000 - ETA: 5:40 - loss: 2.8732 - acc: 0.1458448/50000 - ETA: 5:20 - loss: 2.8842 - acc: 0.1406.........49664/50000 - ETA: 1s - loss: 1.5160 - acc: 0.461149728/50000 - ETA: 1s - loss: 1.5157 - acc: 0.461249792/50000 - ETA: 1s - loss: 1.5153 - acc: 0.461449856/50000 - ETA: 0s - loss: 1.5147 - acc: 0.461549920/50000 - ETA: 0s - loss: 1.5144 - acc: 0.461749984/50000 - ETA: 0s - loss: 1.5141 - acc: 0.461750000/50000 - 262s 5ms/step - loss: 1.5140 - acc: 0.4618 - val_loss: 1.0715 - val_acc: 0.6195End of Epoch 1

Notera att du i de flesta fall vill ha en valideringsuppsättning som skiljer sig från testuppsättningen, och därför anger du en procentandel av träningsdata som ska användas som valideringsuppsättning. I det här fallet skickar vi bara in testdata för att se till att testdata sätts åt sidan och inte tränas på. Vi kommer bara att ha testdata i det här exemplet för att hålla det enkelt.

Nu kan vi utvärdera modellen och se hur den presterade. Det är bara att ringa model.evaluate():

# Model evaluationscores = model.evaluate(X_test, y_test, verbose=0)print("Accuracy: %.2f%%" % (scores*100))

Och vi möts av resultatet:

Accuracy: 83.01%

Och det var allt! Vi har nu en tränad CNN för bildigenkänning. Inte dåligt för den första körningen, men du skulle förmodligen vilja leka lite med modellens struktur och parametrar för att se om du inte kan få bättre prestanda.

Slutsats

Nu när du har implementerat ditt första bildigenkänningsnätverk i Keras vore det en bra idé att leka lite med modellen och se hur det påverkar prestandan om du ändrar dess parametrar.

Detta kommer att ge dig en viss intuition om vilka val som är bäst för olika modellparametrar. Du bör också läsa på om de olika valen av parametrar och hyperparametrar medan du gör det. När du känner dig bekväm med dessa kan du försöka implementera din egen bildklassificator på ett annat dataset.

Om du vill leka med koden eller helt enkelt studera den lite djupare, finns projektet uppladdat på GitHub!