Tripla pitagoreică

septembrie 2, 2021
| Niciun comentariu
Geometrie > Geometrie plană > Triunghiuri > Proprietăți ale triunghiurilor >
Teoria numerelor >. DiophantineEquations >
MathWorld Contributors > Knott >
MathWorld Contributors > Noe >

Less…

DOWNLOAD Mathematica NotebookContribuie la această intrare

Un triplu pitagoreic este un triplu de numere întregi pozitive a, b și c astfel încât să existe un triunghi dreptunghic cu picioarele a,b și ipotenuza c. Prin teorema lui Pitagora, acest lucru este echivalent cu găsirea numerelor întregi pozitive a, b și c care să satisfacă

a^2+b^2=c^2.
(1)

Cea mai mică și cea mai cunoscută triplă pitagoreică este (a,b,c)=(3,4,5). Triunghiul dreptunghic având aceste lungimi ale laturilor se numește uneori triunghiul 3, 4, 5.

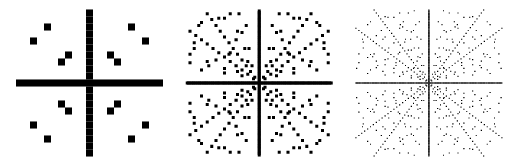
PythagoreanTriples

Ploacele punctelor din planul (a,b) astfel încât (a,b,sqrt(a^2+b^2)) să fie o triplă pitagoreică sunt prezentate mai sus pentru limite succesiv mai mari. Aceste diagrame includ valorile negative ale lui a și b și, prin urmare, sunt simetrice atât în raport cu axa x, cât și cu axa y.

PythagoreanTriplesAC

În mod similar, diagramele punctelor din planul (a,c) astfel încât (a,sqrt(c^2-a^2),c) este un triplu pitagoreic sunt prezentate mai sus pentru limite succesiv mai mari.

PrimitivePythagoreanTriple

Se obișnuiește să se considere doar triplele pitagoreice primitive (numite și triple „reduse”) în care a și b sunt relativ prime, deoarece alte soluții pot fi generate trivial din cele primitive. Triplurile primitive sunt ilustrate mai sus și se poate observa imediat că liniile radiale corespunzătoare triplurilor primitive din graficul original sunt absente în această figură. Pentru soluțiile primitive, una dintre a sau b trebuie să fie pară, iar cealaltă impară (Shanks 1993, p. 141), cu c întotdeauna impară.

În plus, o latură a fiecărei triple pitagoreice este divizibilă cu 3, alta cu 4 și alta cu 5. O latură poate avea doi dintre acești divizori, ca în (8, 15, 17), (7, 24, 25) și (20, 21, 29), sau chiar toți trei, ca în (11, 60, 61).

Dată o triplă primitivă (a_0,b_0,c_0), se obțin trei noi triple primitive din

(a_1,b_1,c_1) = (a_0,b_0,c_0)U
(2)
(a_2,b_2,c_2) = (a_0,b_0,c_0)A
(3)
(a_3,b_3,c_3) = (a_0,b_0,c_0)D,
(4)

unde

.

U =
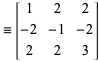(5)
A =
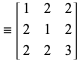(6)
D =.
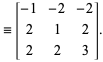(7)

Hall (1970) și Roberts (1977) demonstrează că (a,b,c) este o triplă pitagoreică primitivă dacă

(a,b,c)=(3,4,5)M,
(8)

unde M este un produs finit al matricelor U, A, D. Prin urmare, rezultă că fiecare triplă pitagoreică primitivă trebuie să fie un membru al matricei infinite

( 7, 24, 25); ( 5, 12, 13) ( 55, 48, 73); ( 45, 28, 53); ( 39, 80, 89); (3, 4, 5) ( 21, 20, 29) ( 119, 120, 169); ( 77, 36, 85); ( 33, 56, 65); ( 15, 8, 17) ( 65, 72, 97); ( 35, 12, 37).
(9)

Pitagora și babilonienii au dat o formulă de generare a triplurilor (nu neapărat primitive) ca

(2m,m^2-1,m^2+1),
(10)

pentru m1, care generează un set de triple distincte care nu conține nici toate triplurile primitive, nici toate triplurile imprimitive (și unde în cazul special m=2, m^2-12m).

Primarii greci au dat

(v^2-u^2,2uv,u^2+v^2),
(11)

unde u și vu sunt relativ prime și de paritate opusă (Shanks 1993, p. 141), ceea ce generează un set de triple distincte care conține exact triplele primitive (după sortarea corespunzătoare a v^2-u^2 și 2uv).

Să fie F_n un număr Fibonacci. Atunci

(F_nF_(n+3),2F_(n+1)F_(n+2),F_(n+1)^2+F_(n+2)^2)
(12)

generează triple pitagoreice distincte (Dujella 1995), deși nu în mod exhaustiv nici pentru triplele primitive, nici pentru cele imprimitive. Mai general, pornind de la numerele întregi pozitive a, b, și construind secvența de tip Fibonacci {F_n^'} cu termenii a, b, a+b, a+2b, 2a+3b, … generează triple pitagoreice distincte

(F_n^'F_(n+3)^',2F_(n+1)^'F_(n+2)^',F_(n+1)^'^2+F_(n+2)^'^2)
(13)

(Horadam 1961), unde

F_n^'=1/2 pentru a_0=0; 1/2 pentru a_0=1
(24)

(Beiler 1966, p. 116). Observați că L(s)=1 dacă s este prim sau de două ori prim. Primele numere pentru s=1, 2, … sunt 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1, 1, 4, 1, … (OEIS A046079).

Pentru a afla numărul de moduri H_p(s) în care un număr s poate fi ipotenuza unui triunghi dreptunghic primitiv, scrieți factorizarea sa sub forma

s=2^(a_0)(p_1^(a_1)...p_n^(a_n))(q_1^(b_1)...q_r^(b_r)),
(25)

unde ps sunt de forma x-1, iar qs sunt de forma 4x+1. Numărul de triunghiuri dreptunghice primitive posibile este atunci

H_p(s)={2^(r-1) pentru n=0 și a_0=0; 0 în caz contrar,.
(26)

De exemplu, H_p(65)=2 întrucât

.

65^2 = 16^2+63^2
(27)
= 33^2+56^2.
(28)

Valorile lui H_p(n) pentru n=1, 2, … sunt 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, … (OEIS A024362). Primele numere prime de forma 4x+1 sunt 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, … (OEIS A002144), deci cele mai mici lungimi ale laturilor care sunt ipotenuzele triunghiurilor dreptunghice primitive 1, 2, 4, 8, 16, … sunt 5, 65, 1105, 32045, 1185665, 48612265, … (OEIS A006278).

Numărul triunghiurilor dreptunghice primitive sau neprimitive posibile având ca ipotenuză s este

.

H(s) = 1/2
(29)
= 1/8
(30)

(corectând greșeala de scriere din Beiler 1966, p. 117, care afirmă că această formulă oferă doar numărul de soluții neprimitive), unde r_k(n) este funcția sumă de pătrate. De exemplu, există patru triunghiuri întregi distincte cu ipotenuza 65, deoarece

65^2=16^2+63^2=25^2+60^2=33^2+56^2=39^2+52^2.
(31)

Primele numere pentru s=1, 2, … sunt 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, … (OEIS A046080). Cele mai mici ipotenuze care au n triple distincte sunt 1, 5, 25, 25, 125, 65, 3125, … (OEIS A006339). Tabelul următor prezintă ipotenuzele pentru care există exact n triunghiuri drepte întregi distincte pentru n=0, 1, …, 5.

n OEIS hipotecile pentru care există n triunghiuri întregi distincte
0 A004144 1, 2, 3, 4, 6, 7, 8, 8, 9, 11, 12, 14, 16, 18, ….
1 A084645 5, 10, 13, 15, 17, 20, 26, 29, 30, 34, 35, …
2 A084646 25, 50, 75, 100, 150, 169, 175, 200, 225, ….
3 A084647 125, 250, 375, 500, 750, 875, 1000, 1125, 1375, …
4 A084648 65, 85, 130, 145, 170, 185, 195, 205, 221, 255, …
5 A084649 3125, 6250, 9375, 12500, 18750, 21875, 25000, …

Din acest motiv, numărul total de moduri în care s poate fi fie un picior, fie ipotenuza unui triunghi dreptunghic este dat de

T(s)=L(s)+H(s).
(32)

Valorile pentru s=1, 2, … sunt 0, 0, 1, 1, 1, 2, 1, 1, 1, 1, 2, 2, 2, 2, 1, 1, 4, 2, 2, 1, 5, 3, … (OEIS A046081). Cele mai mici numere s care pot fi laturile unor T triunghiuri dreptunghice generale pentru T=1, 2, … sunt 3, 5, 16, 12, 15, 125, 24, 40, … (OEIS A006593; Beiler 1966, p. 114).

Există 50 de triple pitagoreice cu ipotenuza mai mică de 100, dintre care primele, ordonate crescător c, sunt (3, 4, 5), (6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083, A046084 și A009000).

Dintre acestea, doar 16 sunt triplete primitive cu ipotenuza mai mică de 100: (3, 4,5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65), (16, 63, 65), (48, 55, 73), (36, 77, 85), (13, 84, 85), (39, 80, 89) și (65, 72, 97) (OEIS A046086, A046087 și A020882).

Să se noteze numărul de triple cu ipotenuza N prin Delta(N), numărul de triple cu ipotenuza =N prin Delta^'(N), iar numărul de triple primitive mai mici decât N prin Delta_p(N). Apoi, tabelul următor sintetizează valorile pentru puterile lui 10.

Delta OEIS Delta(10), Delta(10^2), …
Delta(N) A101929 1, 50, 878, 12467, …
Delta^'(N) A101930 2, 52, 881, 12471, …
Delta^'(N) A101930 2, 52, 881, 12471, ….
Delta_p(N) A101931 1, 16, 158, 1593, …

Lehmer (1900) a demonstrat că numărul de soluții primitive cu ipotenuza mai mică decât N satisface

lim_(N-infty)(Delta_p(N))/N=1/(2pi)=0,1591549...
(33)

(OEIS A086201).

PythagoreanIncircles

Inradiile primelor câteva triunghiuri pitagoreice primitive ordonate crescător c sunt date de 1, 2, 3, 3, 3, 6, 5, 4, 4, 10, 5, … (OEIS A014498).

Există o metodă generală de obținere a tripletelor de triunghiuri pitagoreice cu arii egale. Se iau cele trei seturi de generatoare ca

.

.

.

.

m_1 = r^2+rs+s^2
(34)
n_1 = r^2-s^2
(35)
m_2 = r^2+rs+s^2
(36)
n_2 = 2rs+s^2 2rs+s^2
(37)
m_3 = r^2+2rs
(38)
n_3 = r^2+rs+s^2.
(39)

Apoi triunghiul dreptunghic generat de fiecare triplă (m_i^2-n_i^2,2m_in_i,m_i^2+n_i^2) are aria comună

A=rs(2r+s)(r+2s)(r+s)(r+s)(r-s)(r^2+rs+s^2)
(40)

(Beiler 1966, pp. 126-127). Singurul extremum al acestei funcții apare la (r,s)=(0,0). Deoarece A(r,s)=0 pentru r=s, cea mai mică arie comună a trei triunghiuri dreptunghice neprimitive este dată de (r,s)=(1,2), ceea ce duce la o arie de 840 și corespunde tripletelor (24, 70, 74), (40, 42, 58) și (15, 112, 113) (Beiler 1966, p. 126).

Triunghiurile dreptunghice ale căror arii constau dintr-o singură cifră includ (3,4,5) (aria de 6) și (693,1924,2045) (aria de 666666; Wells 1986, p. 89).

În 1643, Fermat l-a provocat pe Mersenne să găsească un triplet pitagoreic a cărui ipotenuză și sumă a catetelor să fie pătrate. Fermat a găsit cea mai mică soluție de acest fel:

.

X = 4565486027761
(41)
Y = 1061652293520
(42)
Z = 4687298610289,
(43)

cu

.

Z =
(44)
X+Y = 2372159^2.
(45)

O problemă conexă este de a determina dacă un număr întreg specificat N poate fi aria unui triunghi dreptunghic cu laturile raționale. 1, 2, 3 și 4 nu sunt ariile niciunui triunghi dreptunghic cu laturile raționale, dar 5 este (3/2, 20/3, 41/6), la fel ca și 6 (3, 4, 5). Soluția problemei implică curba eliptică

y^2=x^3-N^2x.
(46)

O soluție (a, b, c) există dacă (46) are o soluție rațională, caz în care

x = 1/4c^2
(47)
y = 1/8(a^2-b^2)c
(48)

(Koblitz 1993). Nu se cunoaște o metodă generală pentru a determina dacă există o soluție pentru N arbitrară, dar o tehnică elaborată de J. Tunnell în 1983 permite excluderea anumitor valori (Cipra 1996).

.

Articles