Peste 90% din solidele naturale și artificiale sunt cristaline. Majoritatea solidelor se formează cu o dispunere regulată a particulelor lor deoarece interacțiunile atractive globale dintre particule sunt maximizate, iar energia intermoleculară totală este minimizată, atunci când particulele se împachetează în modul cel mai eficient. Aranjamentul regulat la nivel atomic este adesea reflectat la nivel macroscopic. În acest modul, vom explora unele detalii despre structurile solidelor cristaline metalice și ionice și vom învăța cum se determină experimental aceste structuri.

Structurile metalelor

Vom începe discuția noastră despre solidele cristaline luând în considerare metalele elementare, care sunt relativ simple deoarece fiecare conține un singur tip de atom. Un metal pur este un solid cristalin cu atomi de metal împachetați strâns împreună într-un model repetitiv. Unele dintre proprietățile metalelor în general, cum ar fi maleabilitatea și ductilitatea lor, se datorează în mare parte faptului că au atomi identici dispuși într-un model regulat. Proprietățile diferite ale unui metal în comparație cu un altul depind parțial de dimensiunile atomilor și de specificul aranjamentelor spațiale ale acestora. Vom explora asemănările și diferențele a patru dintre cele mai comune geometrii cristaline ale metalelor în secțiunile care urmează.

Celulele unitare ale metalelor

Structura unui solid cristalin, fie că este un metal sau nu, este cel mai bine descrisă prin luarea în considerare a celei mai simple unități repetitive a acestuia, care este denumită celula sa unitară. Celula unitară este formată din puncte de rețea care reprezintă locațiile atomilor sau ionilor. Întreaga structură constă apoi din această celulă unitară care se repetă în trei dimensiuni, așa cum este ilustrat în figura 1.

Figura 1. O celulă unitară arată locațiile punctelor de rețea care se repetă în toate direcțiile.

Să începem investigația noastră asupra structurii rețelei cristaline și a celulelor unitare cu cea mai simplă structură și cea mai elementară celulă unitară. Pentru a vizualiza acest lucru, imaginați-vă că luați un număr mare de sfere identice, cum ar fi mingile de tenis, și că le aranjați uniform într-un recipient. Cel mai simplu mod de a face acest lucru ar fi de a face straturi în care sferele dintr-un strat se află direct deasupra celor din stratul de mai jos, așa cum este ilustrat în figura 2. Această dispunere se numește structură cubică simplă, iar celula unitară se numește celulă unitară cubică simplă sau celulă unitară cubică primitivă.

Figura 2. Atunci când atomii de metal sunt aranjați cu sferele dintr-un strat direct deasupra sau sub sferele din alt strat, structura rețelei se numește cubică simplă. Observați că sferele sunt în contact.

Într-o structură cubică simplă, sferele nu sunt împachetate atât de strâns pe cât ar putea fi și ele „umplu” doar aproximativ 52% din volumul recipientului. Acesta este un aranjament relativ ineficient și doar un singur metal (poloniul, Po) cristalizează într-o structură cubică simplă. După cum se arată în figura 3, un solid cu acest tip de aranjament este format din planuri (sau straturi) în care fiecare atom intră în contact doar cu cei patru vecini cei mai apropiați din stratul său; un atom aflat direct deasupra sa în stratul de deasupra; și un atom aflat direct sub el în stratul de dedesubt. Numărul de alte particule cu care intră în contact fiecare particulă dintr-un solid cristalin este cunoscut sub numele de numărul său de coordonare. Pentru un atom de poloniu într-o matrice cubică simplă, numărul de coordonare este, prin urmare, șase.

Figura 3. Un atom dintr-o structură de rețea cubică simplă intră în contact cu alți șase atomi, deci are un număr de coordonare de șase.

Într-o rețea cubică simplă, celula unitară care se repetă în toate direcțiile este un cub definit de centrele a opt atomi, așa cum se arată în figura 4. Atomii din colțurile adiacente ale acestei celule unitare se contactează între ei, astfel încât lungimea marginilor acestei celule este egală cu două raze atomice sau cu un diametru atomic. O celulă unitară cubică conține doar părțile din acești atomi care se află în interiorul ei. Deoarece un atom aflat într-un colț al unei celule unitare cubice simple este conținut de un total de opt celule unitare, doar o optime din acest atom se află în interiorul unei celule unitare specifice. Și din moment ce fiecare celulă unitară cubică simplă are câte un atom la fiecare dintre cele opt „colțuri” ale sale, există 8 \ ori \frac{1}{8}=1 atom în interiorul unei celule unitare cubice simple.

Figura 4. O celulă unitară de rețea cubică simplă conține o optime de atom în fiecare dintre cele opt colțuri ale sale, deci conține un atom în total.

Exemplu 1: Calculul razei atomice și al densității atomice pentru metale, Partea 1

Lungimea marginii celulei unitare a poloniului alfa este de 336 pm.

1. Determinați raza unui atom de poloniu.
2. Determinați densitatea poloniului alfa.

Afișați soluția

Poloniul alfa cristalizează într-o celulă unitară cubică simplă:

1. Doi atomi de Po adiacenți intră în contact unul cu celălalt, astfel încât lungimea marginii acestei celule este egală cu două raze atomice Po: l=2r. Prin urmare, raza lui Po este r=\dfrac{\text{l}}{2}=\dfrac{\text{336 pm}}{2}=\text{168 pm}.
2. Densitatea este dată de \text{densitate}=\dfrac{\text{masă}}{\text{volum}}. Densitatea poloniului poate fi găsită prin determinarea densității celulei sale unitare (masa conținută într-o celulă unitară împărțită la volumul celulei unitare). Deoarece o celulă unitară Po conține o optime de atom Po în fiecare dintre cele opt colțuri ale sale, o celulă unitară conține un atom Po.

Masa unei celule unitare Po poate fi găsită prin:

\text{1 celulă unitară Po}\ ori \dfrac{\text{1 atom Po}}{\text{1 celulă unitară Po}}\ ori \dfrac{\text{\text{1 mol Po}}{6.022\times {10}^{23}\text{atomii de Po}}\times \dfrac{208.998\text{g}}{\text{1 mol Po}}=3.47\times {10}^{-22}\text{g}

Volumul unei celule unitare de Po poate fi găsit prin:

V={l}^{3}={(336\times {10}^{-10}\text{cm})}^{3}=3.79\times {10}^{-23}{\text{cm}}^{3}

(Observați că lungimea marginii a fost convertită din pm în cm pentru a obține unitățile de volum obișnuite pentru densitate.)

Din acest motiv, densitatea lui \text{Po}=\dfrac{3.471\ ori {10}^{{-22}\text{g}}}{3,79\ ori {10}^{-23}{\text{cm}}^{3}}={\text{9,16 g/cm}}^{3}

Check Your Learning

Lungimea marginii celulei unitare pentru nichel este de 0,3524 nm. Densitatea Ni este de 8,90 g/cm3. Nichelul cristalizează într-o structură cubică simplă? Explicați.

Arată soluția

Nu. Dacă Ni ar fi cubic simplu, densitatea sa ar fi dată de:

\text{1 atom de Ni}\times \dfrac{\text{1 mol Ni}}{6.022\times {10}^{23}\text{atomi de Ni}}\times \dfrac{58.693\text{g}}{\text{1 mol Ni}}=9.746\times {10}^{-23}\text{g}
V={l}^{3}={(3.524\times {10}^{-8}\text{cm})}^{3}=4.376\times {10}^{-23}{\text{cm}}^{3}

Atunci densitatea de Ni ar fi =\dfrac{9.746\times {10}^{-23}\text{g}}{4.376\times {10}^{-23}{\text{cm}}^{3}}={\text{2.23 g/cm}}^{3}^{3}

Deoarece densitatea reală a Ni nu este apropiată de aceasta, Ni nu formează o structură cubică simplă.

Majoritatea cristalelor metalice reprezintă unul dintre cele patru tipuri majore de celule unitare. Deocamdată, ne vom concentra asupra celor trei celule unitare cubice: cubică simplă (pe care am văzut-o deja), celulă unitară cubică centrată pe corp și celulă unitară cubică centrată pe față – toate acestea fiind ilustrate în figura 5. (Rețineți că există de fapt șapte sisteme de rețele diferite, dintre care unele au mai mult de un tip de rețea, pentru un total de 14 tipuri diferite de celule unitare. Lăsăm geometriile mai complicate pentru mai târziu în acest modul.)

Figura 5. Celulele unitare cubice ale metalelor arată (în figurile de sus) locațiile punctelor de rețea și (în figurile de jos) atomii de metal localizați în celula unitară.

Câteva metale cristalizează într-un aranjament care are o celulă unitară cubică cu atomi în toate colțurile și un atom în centru, așa cum se arată în figura 6. Acest lucru se numește un solid cubic centrat pe corp (BCC). Atomii din colțurile unei celule unitare BCC nu intră în contact între ei, ci intră în contact cu atomul din centru. O celulă unitară BCC conține doi atomi: o optime de atom la fiecare dintre cele opt colțuri ( 8\ ori \frac{1}{8}=1 atom din colțuri) plus un atom din centru. Orice atom din această structură atinge patru atomi din stratul de deasupra sa și patru atomi din stratul de sub el. Astfel, un atom dintr-o structură BCC are un număr de coordinare de opt.

Figura 6. Într-o structură cubică centrată pe corp, atomii dintr-un anumit strat nu se ating între ei. Fiecare atom atinge patru atomi din stratul de deasupra lui și patru atomi din stratul de dedesubt.

Atomii din aranjamentele BCC sunt mult mai eficient împachetați decât într-o structură cubică simplă, ocupând aproximativ 68% din volumul total. Metalele izomorfe cu o structură BCC includ K, Ba, Cr, Mo, W și Fe la temperatura camerei. (Elementele sau compușii care cristalizează cu aceeași structură se spune că sunt izomorfe.)

Multe alte metale, cum ar fi aluminiul, cuprul și plumbul, cristalizează într-un aranjament care are o celulă unitară cubică cu atomi în toate colțurile și în centrele fiecărei fețe, așa cum este ilustrat în figura 7. Acest aranjament se numește un solid cubic cu fețe centrate (FCC). O celulă unitară FCC conține patru atomi: o optime de atom la fiecare dintre cele opt colțuri ( 8 ori \frac{1}{8}=1 atom de la colțuri) și o jumătate de atom pe fiecare dintre cele șase fețe (6 ori \frac{1}{2}=3 atomi de la fețe). Atomii de la colțuri ating atomii din centrele fețelor adiacente de-a lungul diagonalelor fețelor cubului. Deoarece atomii se află pe puncte identice ale rețelei, ei au medii identice.

Figura 7. Un solid cubic cu fețe centrate are atomi la colțuri și, așa cum sugerează și numele, în centrele fețelor celulelor sale unitare.

Atomii dintr-un aranjament FCC sunt împachetați cât mai strâns posibil, atomii ocupând 74% din volum. Această structură se mai numește și împachetarea cea mai apropiată cubică (CCP). În CCP, există trei straturi repetitive de atomi aranjați hexagonal. Fiecare atom intră în contact cu șase atomi din propriul strat, trei din stratul de deasupra și trei din stratul de dedesubt. În acest aranjament, fiecare atom atinge 12 vecini apropiați și, prin urmare, are un număr de coordonare de 12. Faptul că aranjamentele FCC și CCP sunt echivalente poate să nu fie imediat evident, dar motivul pentru care acestea sunt de fapt aceeași structură este ilustrat în figura 8.

Figura 8. Un aranjament CCP este format din trei straturi repetitive (ABCABC…) de atomi dispuși hexagonal. Atomii dintr-o structură CCP au un număr de coordonare de 12, deoarece intră în contact cu șase atomi din stratul lor, plus trei atomi din stratul de deasupra și trei atomi din stratul de dedesubt. Prin rotirea perspectivei, putem vedea că o structură CCP are o celulă unitară cu o față care conține un atom din stratul A într-un colț, atomi din stratul B de-a lungul unei diagonale (la două colțuri și în mijlocul feței) și un atom din stratul C în colțul rămas. Acesta este același lucru cu un aranjament cubic cu fețe centrate.

Pentru că o împachetare mai strânsă maximizează atracțiile globale dintre atomi și minimizează energia intermoleculară totală, atomii din majoritatea metalelor se împachetează în acest mod. Găsim două tipuri de împachetare mai strânsă în structurile cristaline metalice simple: CCP, pe care l-am întâlnit deja, și împachetarea cea mai apropiată hexagonală (HCP), prezentată în figura 9. Ambele constau în straturi repetate de atomi aranjați hexagonal. În ambele tipuri, un al doilea strat (B) este plasat pe primul strat (A), astfel încât fiecare atom din cel de-al doilea strat să fie în contact cu trei atomi din primul strat. Al treilea strat este poziționat într-unul din cele două moduri. În HCP, atomii din cel de-al treilea strat se află direct deasupra atomilor din primul strat (adică al treilea strat este, de asemenea, de tip A), iar suprapunerea constă în alternarea straturilor de tip A și de tip B strâns împachetate (adică ABABAB⋯). În cazul CCP, atomii din cel de-al treilea strat nu se află deasupra atomilor din niciunul dintre primele două straturi (adică al treilea strat este de tip C), iar stivuirea constă în straturi apropiate de tip A, tip B și tip C alternativ (de exemplu, ABCABCABC⋯). Aproximativ două treimi din toate metalele cristalizează în aranjamente cel mai strâns împachetate cu numere de coordonare de 12. Printre metalele care cristalizează într-o structură HCP se numără Cd, Co, Li, Mg, Na și Zn, iar printre metalele care cristalizează într-o structură CCP se numără Ag, Al, Ca, Ca, Cu, Ni, Pb și Pt.

Figura 9. În ambele tipuri de împachetare cea mai apropiată, atomii sunt împachetați cât mai compact posibil. Ambalajul cel mai apropiat hexagonal constă din două straturi alternante (ABABABAB…). Împachetarea cea mai apropiată cubică constă din trei straturi alternante (ABCABCABC…).

Exemplu 2: Calculul razei atomice și al densității pentru metale, Partea 2

Calciul cristalizează într-o structură cubică cu fețe centrate. Lungimea marginii celulei sale unitare este de 558,8 pm.

1. Care este raza atomică a Ca în această structură?
2. Calculați densitatea Ca.

Afișați soluția

Partea 1

Într-o structură FCC, atomii de Ca se contactează între ei de-a lungul diagonalei feței, astfel încât lungimea diagonalei este egală cu patru raze atomice de Ca (d = 4r). Două muchii adiacente și diagonala feței formează un triunghi dreptunghic, cu lungimea fiecărei laturi egală cu 558,8 pm și lungimea ipotenuzei egală cu patru raze atomice de Ca:

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}^{2}\longrightarrow {(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}={(4r)}^{2}

Solving this gives r=\sqrt{\dfrac{{(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}}}{16}}=\text{197,6 pmg pentru o rază de Ca}.

Partea 2

Densitatea este dată de \text{densitate}=\dfrac{\text{masă}}{{text{volum}}. Densitatea calciului poate fi găsită prin determinarea densității celulei sale unitare: de exemplu, masa conținută într-o celulă unitară împărțită la volumul celulei unitare. O celulă unitară de Ca cu fețe centrate are o optime de atom la fiecare dintre cele opt colțuri \left(8\times \dfrac{1}{8}=1\text{ atom}\right) și o jumătate de atom pe fiecare dintre cele șase fețe \left(6\times \dfrac{1}{2}=3\text{ atomi}\right), pentru un total de patru atomi în celulă.

Masa celulei unitare poate fi găsită prin:

\text{1 celulă unitară de Ca}\times \dfrac{\text{4 atomi de Ca}}{\text{1 celulă unitară de Ca}\times \dfrac{\text{1 mol Ca}}{6.022\times {10}^{23}\text{atomi de Ca}}\times \dfrac{40.078\text{g}}{\text{1 mol Ca}}=2.662\times {10}^{-22}\text{g}

Volumul unei celule unitare de Ca poate fi găsit prin:

V={a}^{3}={(558.8\times {10}^{-10}\text{cm})}^{3}=1.745\times {10}^{{-22}}{\text{cm}}^{3}

(Rețineți că lungimea marginii a fost convertită din pm în cm pentru a obține unitățile de volum obișnuite pentru densitate.)

Atunci, densitatea de \text{Ca}=\dfrac{2.662\times {10}^{-22}\text{g}}{1.745\times {10}^{-22}{\text{cm}}^{3}}={\text{1.53 g/cm}}^{3}^{3}

Check Your Learning

Argintul cristalizează într-o structură FCC. Lungimea marginii celulei sale unitare este de 409 pm.

1. Care este raza atomică a Ag în această structură?
2. Calculați densitatea Ag.

Afișați soluțiile

1. 144 pm
2. 10.5 g/cm3

În general, o celulă unitară este definită de lungimile a trei axe (a, b și c) și de unghiurile (α, β și γ) dintre ele, așa cum este ilustrat în figura 10. Axele sunt definite ca fiind lungimile dintre punctele din rețeaua spațială. În consecință, axele celulei unitare unesc puncte cu medii identice.

Figura 10. O celulă unitară este definită de lungimile celor trei axe ale sale (a, b și c) și de unghiurile (α, β și γ) dintre axe.

Există șapte sisteme de zăbrele diferite, dintre care unele au mai multe tipuri de zăbrele, pentru un total de paisprezece celule unitare diferite, care au formele prezentate în figura 11.

Figura 11. Există șapte sisteme reticulare diferite și 14 celule unitare diferite.

Structurile cristalelor ionice

Cristalele ionice sunt formate din două sau mai multe tipuri diferite de ioni care au, de obicei, dimensiuni diferite. Împachetarea acestor ioni într-o structură cristalină este mai complexă decât împachetarea atomilor metalici care au aceeași mărime.

Majoritatea ionilor monatomici se comportă ca sfere încărcate, iar atracția lor pentru ionii de sarcină opusă este aceeași în orice direcție. În consecință, structurile stabile pentru compușii ionici rezultă (1) atunci când ionii de o sarcină sunt înconjurați de cât mai mulți ioni posibil de sarcină opusă și (2) atunci când cationii și anionii sunt în contact unul cu celălalt. Structurile sunt determinate de doi factori principali: dimensiunile relative ale ionilor și raportul dintre numărul de ioni pozitivi și negativi din compus.

Figura 12. Cationii pot ocupa două tipuri de găuri între anioni: găuri octaedrice sau găuri tetraedrice.

În structurile ionice simple, găsim de obicei anionii, care sunt în mod normal mai mari decât cationii, dispuși într-o matrice cât mai bine împachetată. (După cum s-a văzut anterior, electronii suplimentari atrași de același nucleu fac ca anionii să fie mai mari, iar electronii mai puțini atrași de același nucleu fac ca cationii să fie mai mici în comparație cu atomii din care sunt formați). Cationii mai mici ocupă în mod obișnuit unul dintre cele două tipuri de găuri (sau interstiții) rămase între anioni. Cel mai mic dintre găuri se găsește între trei anioni într-un plan și un anion într-un plan adiacent. Cei patru anioni care înconjoară această gaură sunt dispuși la colțurile unui tetraedru, astfel încât gaura se numește gaură tetraedrică. Tipul mai mare de gaură se găsește în centrul a șase anioni (trei într-un strat și trei într-un strat adiacent) situați la colțurile unui octaedru; aceasta se numește gaură octaedrică. Figura 12 ilustrează aceste două tipuri de găuri.

În funcție de dimensiunile relative ale cationilor și anionilor, cationii unui compus ionic pot ocupa găuri tetraedrice sau octaedrice, așa cum este ilustrat în figura 13. Cationii relativ mici ocupă găuri tetraedrice, iar cationii mai mari ocupă găuri octaedrice. În cazul în care cationii sunt prea mari pentru a încăpea în găurile octaedrice, anionii pot adopta o structură mai deschisă, cum ar fi o matrice cubică simplă. Cationii mai mari pot ocupa atunci găurile cubice mai mari, făcute posibile de spațierea mai deschisă.

Figura 13. Dimensiunea unui cation și forma găurii ocupate de compus sunt direct legate.

Există două găuri tetraedrice pentru fiecare anion într-o matrice de anioni HCP sau CCP. Un compus care cristalizează într-o matrice de anioni cel mai strâns împachetată cu cationi în găurile tetraedrice poate avea un raport maxim de cationi:anioni de 2:1; toate găurile tetraedrice sunt ocupate în acest raport. Printre exemple se numără Li2O, Na2O, Li2S și Na2S. Compușii cu un raport mai mic de 2:1 pot, de asemenea, să cristalizeze într-o matrice de anioni cel mai strâns împachetată cu cationi în găurile tetraedrice, dacă dimensiunile ionice se potrivesc. Cu toate acestea, în acești compuși, unele dintre găurile tetraedrice rămân libere.

Raportul dintre găurile octaedrice și anioni într-o structură HCP sau CCP este de 1:1. Astfel, compușii cu cationi în găuri octaedrice într-o matrice de anioni cel mai strâns împachetată pot avea un raport maxim de 1:1 între cationi și anioni. În NiO, MnS, NaCl și KH, de exemplu, toate găurile octaedrice sunt umplute. Rapoarte mai mici de 1:1 sunt observate atunci când unele dintre găurile octaedrice rămân goale.

Într-o matrice cubică simplă de anioni, există o gaură cubică ce poate fi ocupată de un cation pentru fiecare anion din matrice. În CsCl, precum și în alți compuși cu aceeași structură, toate găurile cubice sunt ocupate. Jumătate din găurile cubice sunt ocupate în SrH2, UO2, SrCl2 și CaF2.

Diferite tipuri de compuși ionici cristalizează adesea în aceeași structură atunci când dimensiunile relative ale ionilor lor și stoichiometriile lor (cele două caracteristici principale care determină structura) sunt similare.

Celulele unitare ale compușilor ionici

Mulți compuși ionici cristalizează cu celule unitare cubice, iar noi vom folosi acești compuși pentru a descrie caracteristicile generale ale structurilor ionice.

Când un compus ionic este alcătuit din cationi și anioni de dimensiuni similare într-un raport 1:1, el formează de obicei o structură cubică simplă. Clorura de cesiu, CsCl, (ilustrată în figura 14) este un exemplu în acest sens, Cs+ și Cl- având raze de 174 pm și, respectiv, 181 pm. Ne putem gândi la aceasta ca la ioni de clorură care formează o celulă unitară cubică simplă, cu un ion de cesiu în centru; sau ca la ioni de cesiu care formează o celulă unitară cu un ion de clorură în centru; sau ca la celule unitare cubice simple formate de ioni Cs+ care se suprapun peste celule unitare formate de ioni Cl-. Ionii de cesiu și ionii de clorură se ating de-a lungul diagonalelor corpului celulelor unitare. Un ion de cesiu și un ion de clorură sunt prezenți în fiecare celulă unitară, ceea ce dă stoichiometria l:l cerută de formula pentru clorura de cesiu. Rețineți că nu există nici un punct de rețea în centrul celulei, iar CsCl nu este o structură BCC deoarece un ion de cesiu nu este identic cu un ion clorură.

Figura 14. Compușii ionici cu cationi și anioni de dimensiuni similare, cum ar fi CsCl, formează de obicei o structură cubică simplă. Ei pot fi descriși prin celule unitare cu cationi la colțuri sau cu anioni la colțuri.

Am spus că amplasarea punctelor rețelei este arbitrară. Acest lucru este ilustrat de o descriere alternativă a structurii CsCl în care punctele de rețea sunt situate în centrele ionilor de cesiu. În această descriere, ionii de cesiu sunt localizați pe punctele de rețea în colțurile celulei, iar ionul de clorură este localizat în centrul celulei. Cele două celule unitare sunt diferite, dar descriu structuri identice.

Când un compus ionic este alcătuit dintr-un raport 1:1 de cationi și anioni care diferă semnificativ în mărime, acesta cristalizează de obicei cu o celulă unitară FCC, precum cea prezentată în figura 15. Clorura de sodiu, NaCl, este un exemplu în acest sens, Na+ și Cl- având raze de 102 pm și, respectiv, 181 pm. Ne putem gândi la aceasta ca la ionii de clorură care formează o celulă FCC, cu ioni de sodiu localizați în găurile octaedrice din mijlocul marginilor celulei și în centrul celulei. Ionii de sodiu și de clorură se ating între ei de-a lungul marginilor celulei. Celula unitară conține patru ioni de sodiu și patru ioni de clorură, ceea ce dă stoichiometria 1:1 cerută de formula, NaCl.

Figura 15. Compușii ionici cu anioni care sunt mult mai mari decât cationii, cum ar fi NaCl, formează de obicei o structură FCC. Ele pot fi descrise prin celule unitare FCC cu cationi în găurile octaedrice.

Forma cubică a sulfurii de zinc, blenda de zinc, cristalizează, de asemenea, într-o celulă unitară FCC, așa cum este ilustrat în figura 16. Această structură conține ioni de sulfură pe punctele de rețea ale unei rețele FCC. (Aranjamentul ionilor de sulfură este identic cu aranjamentul ionilor de clorură din clorura de sodiu). Raza unui ion de zinc reprezintă doar aproximativ 40% din raza unui ion de sulfură, astfel încât acești mici ioni Zn2+ sunt localizați în găurile tetraedrice alternante, adică în jumătate din găurile tetraedrice. În celula unitară există patru ioni de zinc și patru ioni de sulfură, ceea ce dă formula empirică ZnS.

Figura 16. ZnS, sulfura de zinc (sau blenda de zinc) formează o celulă unitară FCC cu ioni de sulfură în punctele de rețea și ioni de zinc mult mai mici care ocupă jumătate din găurile tetraedrice din structură.

O celulă unitară de fluorură de calciu, ca cea prezentată în figura 17, este de asemenea o celulă unitară FCC, dar în acest caz, cationii sunt localizați pe punctele de rețea; ionii de calciu echivalenți sunt localizați pe punctele de rețea ale unei rețele FCC. Toate situsurile tetraedrice din rețeaua FCC a ionilor de calciu sunt ocupate de ionii de fluorură. Există patru ioni de calciu și opt ioni de fluorură într-o celulă unitară, ceea ce dă un raport calciu:fluor de 1:2, conform formulei chimice CaF2. O examinare atentă a figurii 17 va dezvălui o matrice cubică simplă de ioni de fluor, cu ioni de calciu în jumătate din găurile cubice. Structura nu poate fi descrisă în termenii unei rețele spațiale de puncte pe ionii de fluor, deoarece ionii de fluor nu au toți medii identice. Orientarea celor patru ioni de calciu în jurul ionilor de fluor diferă.

Figura 17. Fluorura de calciu, CaF2, formează o celulă unitară FCC cu ioni de calciu (verzi) în punctele de rețea și ioni de fluorură (roșii) ocupând toate locurile tetraedrice dintre ei.

Calcularea razelor ionice

Dacă cunoaștem lungimea marginii unei celule unitare a unui compus ionic și poziția ionilor în celulă, putem calcula razele ionice pentru ionii din compus dacă facem presupuneri despre formele și contactele ionice individuale.

Exemplu 5: Calculul razelor ionice

Lungimea marginii celulei unitare a LiCl (structură asemănătoare NaCl, FCC) este 0.514 nm sau 5,14 Å. Presupunând că ionul de litiu este suficient de mic pentru ca ionii de clorură să fie în contact, ca în figura 15, calculați raza ionică pentru ionul de clorură.

Nota: Unitatea de lungime angstrom, Å, este adesea folosită pentru a reprezenta dimensiunile la scară atomică și este echivalentă cu 10-10 m.

Afișați soluția

Pe fața unei celule unitare LiCl, ionii de clorură intră în contact unul cu celălalt de-a lungul diagonalei feței:

Desenând un triunghi dreptunghic pe fața celulei unitare, vedem că lungimea diagonalei este egală cu patru raze de clorură (o rază de la fiecare clorură din colț și un diametru – care este egal cu două raze – de la ionul de clorură din centrul feței), deci d = 4r. Din teorema lui Pitagora, avem:

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}^{2}

ceea ce dă:

\stânga(0,514\text{ nm}\dreapta)^{2}+\stânga(0.514\text{ nm}\right)^{2}={\left(4r\right)}^{2}=16{r}^{2}

Solving this gives:

r=\sqrt{\dfrac{{(0.514\text{nm})}^{2}+{(0.514\text{nm})}^{2}}{16}}=\text{0.182 nm} (1,82 Å) pentru o rază a Cl-

Controlați-vă cunoștințele

Lungimea marginii celulei unitare a KCl (structură asemănătoare NaCl, FCC) este de 6,28 Å. Presupunând un contact anion-cation de-a lungul marginii celulei, calculați raza ionului de potasiu. Raza ionului clorură este de 1,82 Å.

Arată soluția

Raza ionului potasiu este de 1,33 Å.

Este important să ne dăm seama că valorile pentru razele ionice calculate din lungimile marginilor celulelor unitare depind de numeroase ipoteze, cum ar fi o formă sferică perfectă pentru ioni, care sunt, în cel mai bun caz, aproximări. Prin urmare, astfel de valori calculate sunt ele însele aproximative și comparațiile nu pot fi împinse prea departe. Cu toate acestea, această metodă s-a dovedit utilă pentru calcularea razelor ionice din măsurători experimentale, cum ar fi determinările cristalografice cu raze X.

Cristalografia cu raze X

Dimensiunea celulei unitare și aranjamentul atomilor într-un cristal pot fi determinate din măsurători ale difracției razelor X de către cristal, numită cristalografie cu raze X. Difracția este schimbarea direcției de deplasare suferită de o undă electromagnetică atunci când aceasta întâlnește o barieră fizică ale cărei dimensiuni sunt comparabile cu cele ale lungimii de undă a luminii. Razele X sunt radiații electromagnetice cu lungimi de undă aproximativ la fel de mari ca distanța dintre atomii vecini din cristale (de ordinul a câtorva Å).

Când un fascicul de raze X monocromatice lovește un cristal, razele sale sunt împrăștiate în toate direcțiile de către atomii din cristal. Atunci când undele împrăștiate care călătoresc în aceeași direcție se întâlnesc între ele, ele suferă interferențe, un proces prin care undele se combină pentru a produce fie o creștere, fie o scădere a amplitudinii (intensității) în funcție de măsura în care maximele undelor care se combină sunt separate (a se vedea figura 18).

Figura 18. Undele luminoase care ocupă același spațiu suferă interferențe, combinându-se pentru a produce unde de intensitate mai mare (a) sau mai mică (b), în funcție de separarea maximelor și minimelor lor.

Când razele X cu o anumită lungime de undă, λ, sunt împrăștiate de atomii din planuri cristaline adiacente separate de o distanță, d, ele pot suferi interferențe constructive atunci când diferența dintre distanțele parcurse de cele două unde înainte de combinarea lor este un factor întreg, n, al lungimii de undă. Această condiție este îndeplinită atunci când unghiul fasciculului difractat, θ, este legat de lungimea de undă și de distanța interatomică prin ecuația:

n{\lambda }=2d\text{sin}\theta

Această relație este cunoscută sub numele de ecuația Bragg, în onoarea lui W. H. Bragg, fizicianul englez care a explicat primul acest fenomen. Figura 19 ilustrează două exemple de unde difractate din aceleași două planuri cristaline. Figura din stânga descrie undele difractate la unghiul Bragg, rezultând o interferență constructivă, în timp ce cea din dreapta arată difracția și un unghi diferit care nu satisface condiția Bragg, rezultând o interferență distructivă.

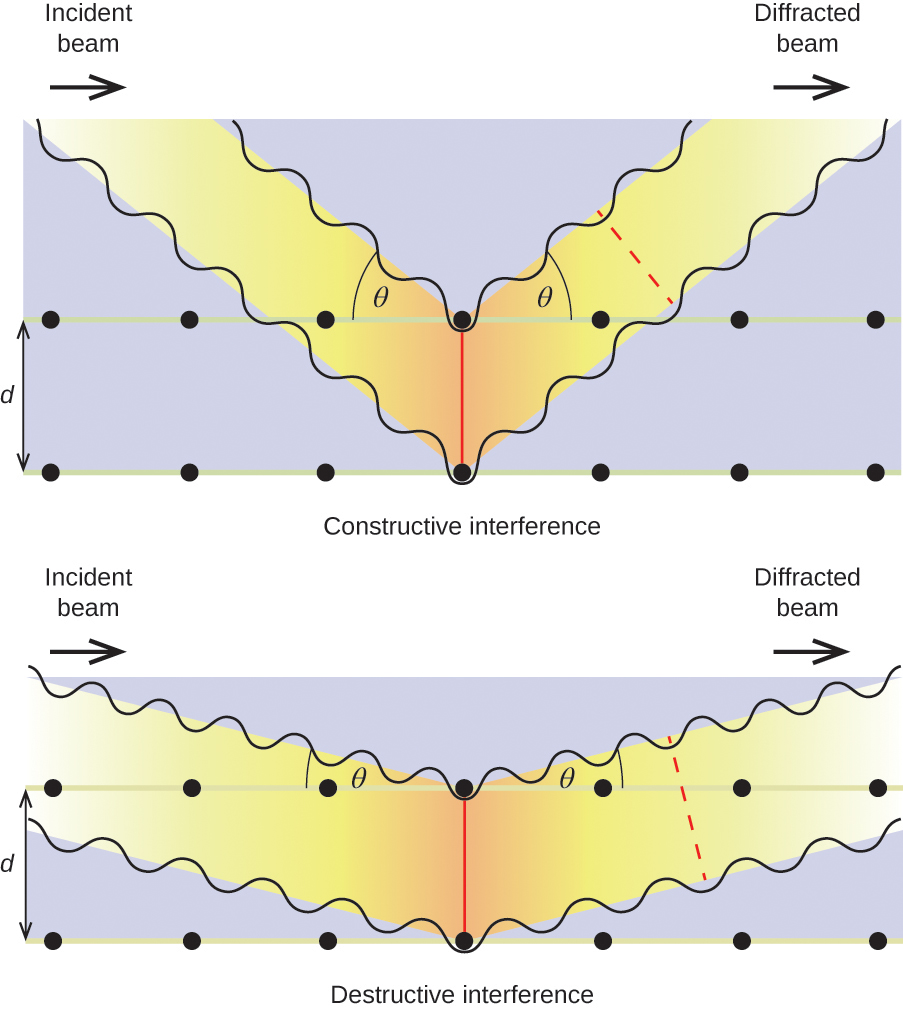
Figura 19. Difracția razelor X împrăștiate de atomii din interiorul unui cristal permite determinarea distanței dintre atomi. Imaginea de sus înfățișează interferența constructivă dintre două unde împrăștiate și o undă difractată rezultată de intensitate mare. Imaginea de jos descrie interferența distructivă și o undă difractată de intensitate scăzută.

Un difractometru de raze X, cum ar fi cel ilustrat în figura 20, poate fi utilizat pentru a măsura unghiurile la care sunt difractate razele X atunci când interacționează cu un cristal, așa cum este descris mai sus. Pornind de la astfel de măsurători, ecuația Bragg poate fi utilizată pentru a calcula distanțele dintre atomi, așa cum se demonstrează în următorul exemplu de exercițiu.

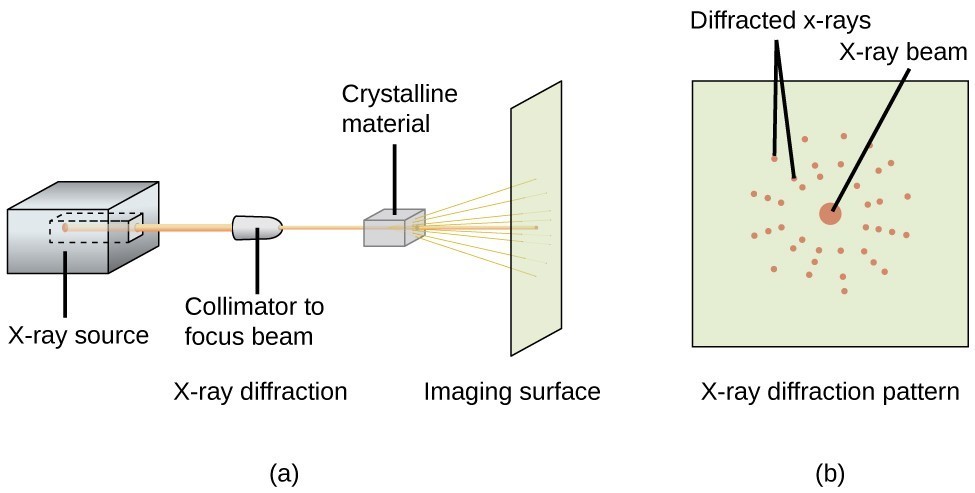
Figura 20. Într-un difractometru (a), un fascicul de raze X lovește un material cristalin, producând un model de difracție a razelor X (b) care poate fi analizat pentru a determina structura cristalină.

Puteți vizualiza transcriptul pentru „Celebrating Crystallography – An animated adventure” aici (se deschide într-o fereastră nouă).

Portretul unui chimist: Cristalograful cu raze X Rosalind Franklin

Figura 21. Această ilustrație arată o imagine de difracție a razelor X similară cu cea pe care Franklin a găsit-o în cercetările sale. (credit: National Institutes of Health)

Descoperirea structurii ADN-ului în 1953 de către Francis Crick și James Watson este una dintre marile realizări din istoria științei. Aceștia au primit Premiul Nobel pentru Fiziologie sau Medicină în 1962, împreună cu Maurice Wilkins, care a furnizat dovada experimentală a structurii ADN-ului. Chimista britanică Rosalind Franklin a adus o contribuție neprețuită la această realizare monumentală prin munca sa de măsurare a imaginilor de difracție cu raze X ale ADN-ului. La începutul carierei sale, cercetările lui Franklin privind structura cărbunilor s-au dovedit utile pentru efortul de război britanic. După ce și-a mutat atenția asupra sistemelor biologice la începutul anilor 1950, Franklin și studentul doctorand Raymond Gosling au descoperit că ADN-ul este format din două forme: o fibră lungă și subțire care se formează atunci când este umedă (tip „B”) și o fibră scurtă și lată care se formează atunci când este uscată (tip „A”). Imaginile sale de difracție cu raze X ale ADN-ului (Figura 21) au furnizat informațiile cruciale care le-au permis lui Watson și Crick să confirme că ADN-ul formează un dublu helix și să determine detaliile dimensiunii și structurii sale.

Franklin a efectuat, de asemenea, cercetări de pionierat asupra virușilor și ARN-ului care conține informația lor genetică, descoperind noi informații care au schimbat radical ansamblul de cunoștințe în acest domeniu. După ce a dezvoltat un cancer ovarian, Franklin a continuat să lucreze până la moartea sa în 1958, la vârsta de 37 de ani. Printre numeroasele recunoașteri postume ale muncii sale, Școala de Medicină din Chicago a Universității Finch de Științe ale Sănătății și-a schimbat numele în Universitatea de Medicină și Știință Rosalind Franklin în 2004 și a adoptat ca logo oficial al universității o imagine a faimoasei sale imagini a ADN-ului prin difracție de raze X.

Glosar

Solid cubic centrat pe corp (BCC): structură cristalină care are o celulă unitară cubică cu puncte de rețea la colțuri și în centrul celulei

celulă unitară cubică centrată pe corp: cea mai simplă unitate de repetiție a unui cristal cubic centrat pe corp; este un cub care conține puncte de rețea la fiecare colț și în centrul cubului

Ecuația Bragg: ecuație care relaționează unghiurile la care razele X sunt difractate de atomii dintr-un cristal

Numărul de coordinare: numărul de atomi cel mai apropiat de un anumit atom dintr-un cristal sau de atomul metalic central dintr-un complex

Cubic closest packing (CCP): structură cristalină în care planurile de atomi sau ioni strâns împachetați sunt stivuite ca o serie de trei straturi alternante cu orientări relative diferite (ABC)

difuzie: redirecționarea radiației electromagnetice care apare atunci când aceasta întâlnește o barieră fizică de dimensiuni corespunzătoare

Solid cubic centrat pe fețe (FCC): structură cristalină formată dintr-o celulă unitară cubică cu puncte de rețea în colțurile și în centrul fiecărei fețe

Celulă unitară cubică centrată pe fețe: cea mai simplă unitate de repetiție a unui cristal cubic cu fețe centrate; este un cub care conține puncte de rețea la fiecare colț și în centrul fiecărei fețe

ambalare hexagonală cea mai apropiată (HCP): structură cristalină în care straturi apropiate de atomi sau ioni sunt stivuite ca o serie de două straturi alternante cu orientări relative diferite (AB)

gaura: (de asemenea, interstițiu) spațiu între atomi în cadrul unui cristal

isomorfă: care posedă aceeași structură cristalină

gaura octaedrică: spațiu deschis într-un cristal în centrul a șase particule situate în colțurile unui octaedru

celulă unitară cubică simplă: (de asemenea, celulă unitară cubică primitivă) celulă unitară din structura cubică simplă

structură cubică simplă: structură cristalină cu o celulă unitară cubică cu puncte de rețea numai la colțuri

rețea spațială: totalitatea punctelor dintr-un cristal care au medii identice

gaura tetraedrică: spațiu tetraedric format de patru atomi sau ioni într-un cristal

celulă unitară: cea mai mică porțiune a unei rețele spațiale care se repetă în trei dimensiuni pentru a forma întreaga rețea

Cristalografie cu raze X: tehnică experimentală pentru determinarea distanțelor dintre atomii dintr-un cristal prin măsurarea unghiurilor la care sunt difractate razele X la trecerea prin cristal

.