Ce rost au tabelele de caractere?

În acest punct, o întrebare bună este: ce rost are să învățăm despre tabelele de caractere? Răspunsul simplu este că simetria și tabelul de caractere asociat unei molecule pot fi folosite pentru a interpreta și prezice multe aspecte ale spectroscopiilor semnificative din punct de vedere chimic, precum și ale legăturilor. Vom ilustra acest lucru în cele ce urmează, concentrându-ne asupra modurilor vibraționale ale unei molecule.

În laborator putem aduna date experimentale utile folosind spectroscopia în infraroșu (IR) și Raman. Aceste date pot fi comparate cu numărul de benzi active IR și/sau Raman prezise în urma aplicării teoriei grupurilor și a tabelului corect al caracterelor. Matematica (teoria grupurilor și algebra matricială) care stă la baza acestui tratament servește ca bază teoretică solidă. Manipulările descrise mai jos funcționează deoarece toate operațiile de simetrie ale unei molecule cuprind un grup matematic și se supun regulilor grupului. După cum s-a menționat anterior, nu trebuie să stăpânim acest domeniu al matematicii pentru a utiliza bine tabelele de caractere.

Degrese de libertate și vibrații în molecule

Aici vom discuta inițial despre gradele de libertate pentru o moleculă simplă (apa). Vom vedea foarte repede de ce este foarte benefică utilizarea simetriei atunci când investigăm molecule mai mari.

Pentru o moleculă cu „N” atomi există 3N grade de libertate (amintiți-vă că trăim într-o lume tridimensională de coordonate x, y, z). Pentru o moleculă neliniară 3 grade de libertate pot fi semnate la translații – mișcarea unui corp în ansamblu (Tx, Ty, Tz) și 3 la rotații (Rx, Ry, Rz). Celelalte mișcări ale atomilor sunt deplasări ale atomilor față de pozițiile lor medii – centrul de greutate nu se modifică. Aceste vibrații fundamentale sunt denumite „moduri normale”. Astfel, o moleculă neliniară are 3N-6 moduri normale. Pentru apă, numărul de moduri normale este 3 (3 x 3 – 6 = 3). Pentru moleculele liniare există 3N-5 moduri normale.

Pentru apă, care, desigur, a fost intens studiată, știm că cele 3 vibrații sunt următoarele.

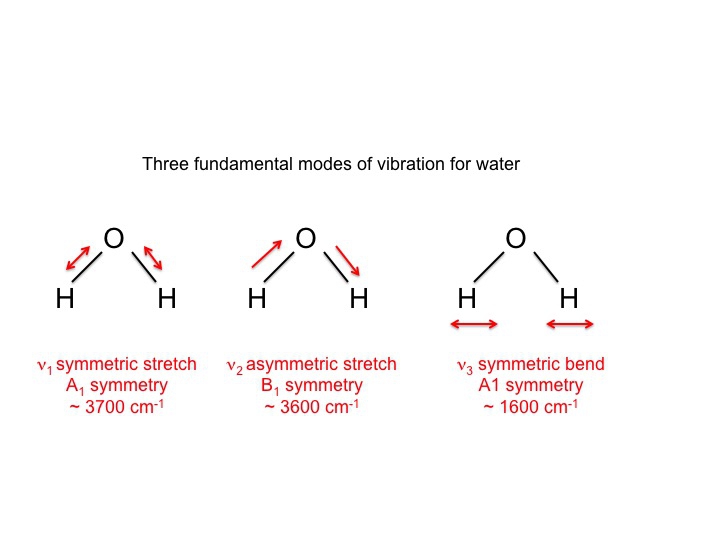
Simbolurile folosite pentru a descrie aceste moduri (A1, B1) sunt aceleași simboluri Mulliken pe care le-am întâlnit în discuția noastră despre tabelele de caractere. Cu alte cuvinte, vibrațiile, care sunt proprietăți moleculare, pot fi descrise prin specii de simetrie sau reprezentări ireductibile. De fapt, o mare parte din literatura de specialitate care implică spectroscopia vibrațională folosește aceste simboluri ca o modalitate prescurtată de comunicare a informațiilor.

Ar trebui să fie destul de evident că numărul de vibrații crește rapid chiar și cu creșteri modeste ale numărului de atomi din moleculă. Determinarea tipurilor de vibrații prin inspecție (așa cum am făcut pentru apă) devine acum mult mai dificilă. De exemplu, luați în considerare următorii compuși:

H2O 3 atomi 3 vibrații

PH3 4 atomi 6 vibrații

CO22-. 4 atomi 6 vibrații

XeF4 5 atomi 9 vibrații

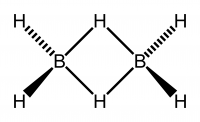
B2H6 8 atomi 18 vibrații

Pentru diboran (B2H6) care are simetria D2h aflarea naturii și a speciei de simetrie a tuturor celor 18 vibrații prin inspecție ar fi o sarcină descurajantă. Cu toate acestea, înarmați cu tabelul de caractere pentru D2h și cunoașterea proprietăților de simetrie, sarcina de a determina specia de simetrie a tuturor vibrațiilor este simplă.

Pentru cazul apei am putea prezenta tabelul de caractere (C2v) cu cele 3 vibrații (ν1, v2, v3) enumerate în coloana proprietăților moleculare, așa cum se arată mai jos. (ν = simbolul grecesc „nu”)

Cu toate acestea, în general, această abordare este nepractică. Să luăm ca exemplu piridina (C5H5N). Grupa punctiformă este, de asemenea, C2v, dar molecula are 11 atomi. Numărul de moduri fundamentale de vibrație este de 27 ( 3 x 11 – 6 = 27).

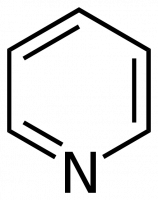
În acest caz ar trebui să întocmim un tabel de caractere C2v care să prezinte simetriile tuturor celor 27 de vibrații. Din acest motiv, vibrațiile nu sunt în mod normal incluse în tabelele de caractere. În schimb, este la latitudinea utilizatorului (dumneavoastră) să determine numărul și tipul de vibrații (așa cum sunt definite de speciile lor de simetrie) pentru toate moleculele pe care le întâlnește. Modul în care facem acest lucru este descris mai jos.

Reprezentări Redutabile

După cum s-a menționat anterior, una dintre proprietățile importante ale tabelelor de caractere este că operațiile de simetrie sunt membre ale unui grup matematic și există relații importante între ele. În general, același lucru se poate spune și despre speciile de simetrie sau reprezentările ireductibile ale proprietăților moleculare. Produsele rezultate din combinarea caracterelor reprezentărilor ireductibile, fie prin înmulțire, fie prin adunare/substracție, se supun, de asemenea, regulilor grupului. Noile reprezentări nu mai sunt cele mai simple posibile și sunt denumite „reprezentări reductibile”, deoarece pot fi „reduse” la părțile lor componente.

De exemplu, pentru apă, simetriile de translație (Tx, Ty, Tz) pot fi desprinse direct din tabelul de caractere C2v. Acestea sunt A1, B1 și B2. Putem reprezenta toate aceste trei grade de libertate printr-o reprezentare ΓT și putem scrie expresia de mai jos. (Γ = litera grecească majusculă „gamma”).

ΓT = A1 + B1 + B2

Știm că A1, B1 și B2 sunt doar notații prescurtate pentru speciile de simetrie (reprezentări ireductibile). Prin urmare, putem scrie pur și simplu caracterele lui ΓT prin adăugarea caracterelor individuale pentru A1, B1 și B2 din tabelul de caractere C2v.

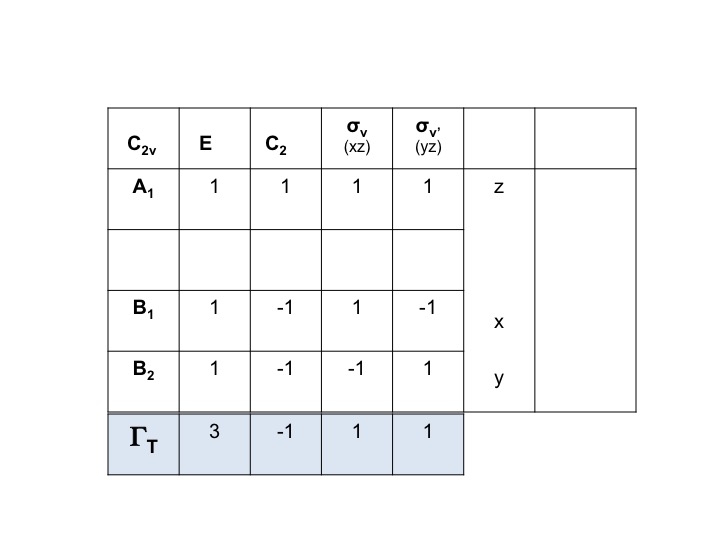
Atunci ΓT = 3 -1 1 1 1.

Aceasta este o reprezentare redutabilă validă și un membru al grupului C2v.

În mod similar putem scrie reprezentarea redutabilă pentru toate cele trei rotații și toate vibrațiile.

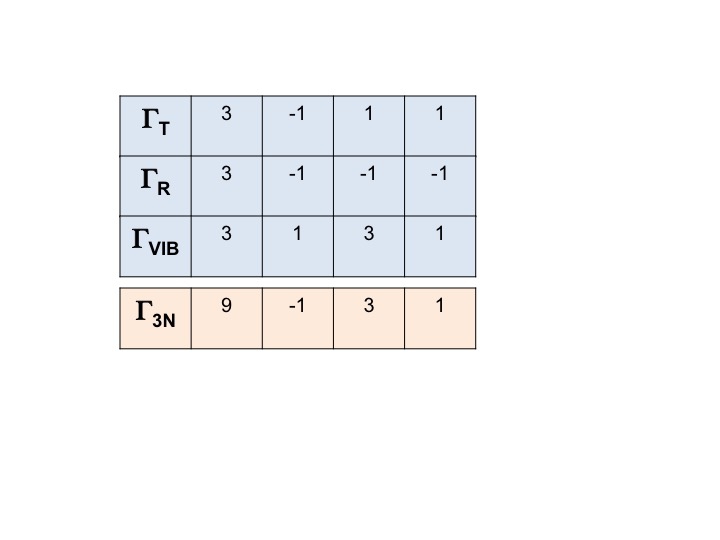
Reprezentarea pentru TOATE gradele de libertate pentru molecula (3N) poate fi scrisă sub forma

Γ3N = ΓT + ΓR + ΓVIB

și reprezentarea redutabilă pentru aceasta se obține prin simpla însumare a caracterelor pentru ΓT, ΓR și ΓVIB.

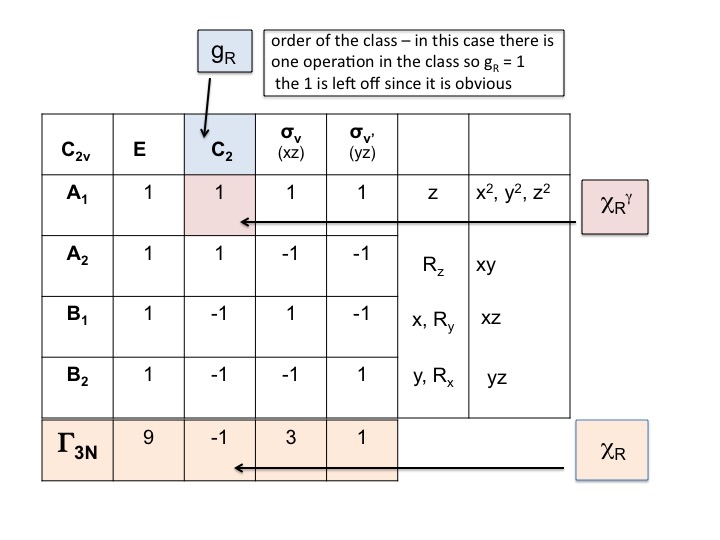
Γ3N = 9 -1 3 1

Rețineți acest lucru – va apărea mai târziu!

Deși setul de caractere 9 -1 3 1 este un membru valabil al grupului C2v, acesta nu este deosebit de util atunci când se discută despre proprietățile moleculare. Ceea ce este cu adevărat necesar este limbajul speciilor de simetrie stenografiată (simbolurile Mulliken, A1, B1 etc.). Cu alte cuvinte, dorim să exprimăm Γ3N în termeni de A1, B1 etc. Din informațiile acoperite mai sus se poate arăta cu ușurință prin inspecție că:

Γ3N = 3A1 +A2 + 3B1 +2B2

Veste bună este că pentru alte molecule mai complexe nu trebuie să efectuăm această sarcină prin inspecție deoarece:

1. Putem genera cu ușurință Γ3N ca reprezentare redutabilă pentru o moleculă (dacă îi cunoaștem simetria grupului punctiform).

2. Putem converti cu ușurință reprezentarea redutabilă Γ3N în suma speciilor sale de simetrie (simboluri Mulliken) folosind o formulă „simplă” cunoscută sub numele de formula de reducere.

Metoda generală de obținere a Γ3N

Pasul 1

Se ia tabelul de caractere pentru moleculă și se adaugă un rând în partea de jos. În acest rând generați reprezentarea redutabilă pentru ΓT (sau Γxyz) așa cum am făcut mai sus, pur și simplu adăugând caracterele pentru fiecare operație care corespund proprietăților moleculare pentru x, y și z. Pentru C2v am arătat deja că acestea sunt caracterele care corespund lui A1, B1 și B2.

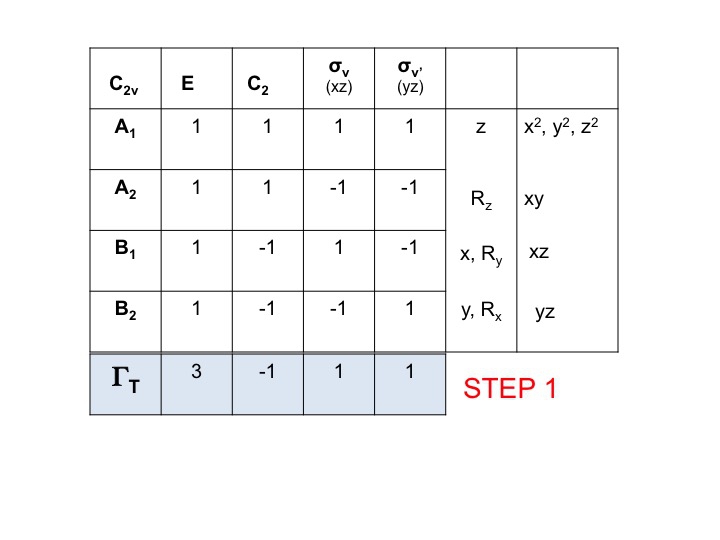
Pasul 2

Adaugați un alt rând sub ΓT și notați numărul de atomi care NU-și SCHIMBĂ poziția în timpul fiecărei operații de simetrie. Acesta este momentul în care vă dați seama cât de util este un set de modele moleculare reale. Pentru a face acest lucru, va trebui, de asemenea, să știți unde se află elementele de simetrie și cum afectează molecula operațiile de simetrie. Desigur, știți deja cum să faceți acest lucru, deoarece ați studiat notația Schönflies și știți cum să atribuiți grupul de puncte al unei molecule. Tabelul de caractere are, de asemenea, toate operațiile de simetrie listate în funcție de clasă de-a lungul rândului de sus.

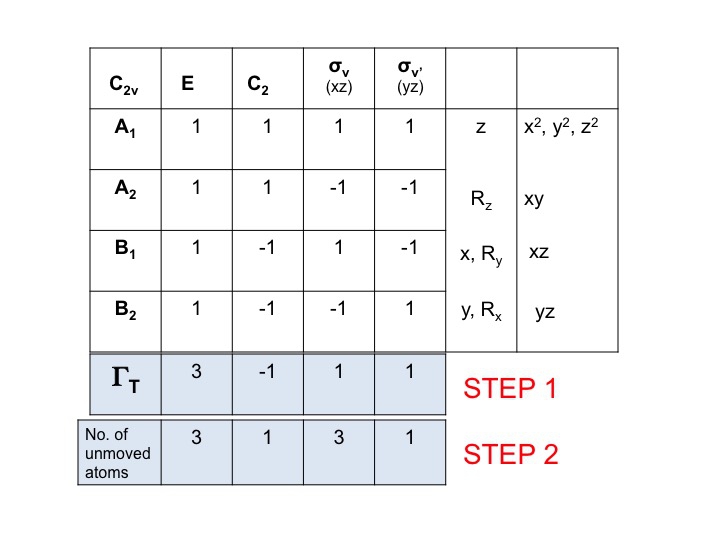
Așa, pentru apă (3 atomi) sub E sunt 3 atomi nemișcați, dar pentru C2 ambii H se mișcă, dar cum atomul O stă pe axa C2 nu-și schimbă poziția și astfel înregistrăm 1 sub coloana C2. Noul set de numere generat în etapa 2 (3 1 3 3 1) este, de asemenea, o reprezentare redutabilă în C2v și se supune regulilor grupului.

Etapa 3

În această etapă pur și simplu înmulțim împreună caracterele care au fost generate în etapele 1 și 2. Rezultatul (al treilea rând) este reprezentarea redutabilă pentru Γ3N (sau ΓTOT). Este atât de simplu.

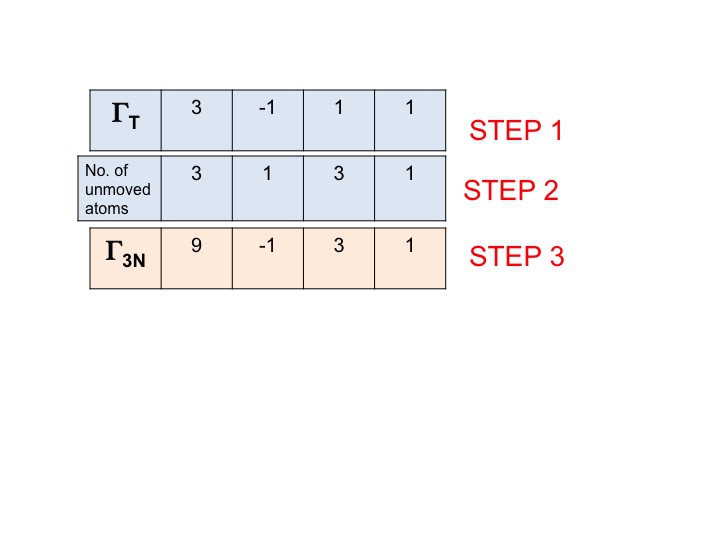
Vă veți observa că noua reprezentare redutabilă (9 -1 1 1 3) este identică cu reprezentarea pentru Γ3N pe care am obținut-o anterior prin inspecție.

Reducerea reprezentării reductibile

Pentru a converti ORICE reprezentare reductibilă în suma reprezentărilor sale ireductibile (specii de simetrie sau simboluri Mulliken) folosim o formulă de reducere:

Puteți găsi cu ușurință această informație în tabelul de caractere:

Înapoi la exemplul nostru pentru apă: Grupa punctiformă C2v, ordin (g) = 4

Reprezentarea redutabilă pentru Γ3N = 9 -1 3 1

Numărul de apariții ale lui A1 în această reprezentare este deci

aA1 = 1/4 { 1,1,9 + 1,1. (-1) + 1.1.3 +1.1.1} = 3

deci Γ3N conține 3 specii de simetrie A1. Numărul celorlalte specii de simetrie se calculează după cum urmează:

aA2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1).3 + 1.(-1).1 } = 1 o specie A2 prezentă

aB1 = 1/4 { 1.1.9 + 1.(-1).(-1) + 1.1.3 + 1.(-1).1}. = 3 3 3 B1 prezent

aB2 = 1/4 {1.1.9 + 1.(-1)(-1)(-1) + 1.(-1).3 + 1.1.1} = 2 2 2 B2 prezent

Acum putem scrie Γ3N = 3A1 + A2 + 3B1 + 2B2 (exact ceea ce am obținut prin „inspecția” de mai sus. Putem acum să scădem speciile de simetrie pentru translații și rotații și astfel vom obține numărul și speciile de simetrie ale modurilor fundamentale de vibrație. ΓT și ΓR pot fi obținute direct din tabelul de caractere.

Γ3N = 3A1 + A2 + 3B1 + 2B2

ΓT = A1 + B1 + B2

ΓR = A2 + B1 + B2

ΓVIB = Γ3N – ΓT – ΓR = 2A1 +B1

Înseamnă că cele trei moduri normale de vibrație pentru apă au simetriile A1, A1 și B1.

Dispunem acum de o metodă generală de determinare a tuturor modurilor fundamentale de vibrație pentru o moleculă și de exprimare a acestor moduri în limbajul prescurtat al simbolurilor Mulliken. Acesta este unul dintre exercițiile la care veți fi testați la examenul 1. Cel mai bun mod de a deveni încrezător în această metodă este să exersați cât mai multe exemple posibile!

Urmatorul: Reguli de selecție

.