Química para mayores

agosto 5, 2021
| No hay comentarios

Resultados de aprendizaje

  • Describir la disposición de los átomos e iones en las estructuras cristalinas
  • Calcular los radios iónicos utilizando las dimensiones de la celda unitaria
  • Explicar el uso de las mediciones de difracción de rayos X para determinar las estructuras cristalinas

Más del 90% de los sólidos naturales y artificiales son cristalinos.de rayos X para determinar las estructuras cristalinas

Más del 90% de los sólidos naturales y artificiales son cristalinos. La mayoría de los sólidos se forman con una disposición regular de sus partículas porque las interacciones atractivas globales entre las partículas se maximizan, y la energía intermolecular total se minimiza, cuando las partículas se empaquetan de la manera más eficiente. La disposición regular a nivel atómico suele reflejarse a nivel macroscópico. En este módulo, exploraremos algunos de los detalles sobre las estructuras de los sólidos cristalinos metálicos e iónicos, y aprenderemos cómo se determinan estas estructuras experimentalmente.

Las estructuras de los metales

Empezaremos nuestra discusión sobre los sólidos cristalinos considerando los metales elementales, que son relativamente simples porque cada uno contiene sólo un tipo de átomo. Un metal puro es un sólido cristalino con átomos metálicos empaquetados estrechamente en un patrón repetitivo. Algunas de las propiedades de los metales en general, como su maleabilidad y ductilidad, se deben en gran medida a que tienen átomos idénticos dispuestos en un patrón regular. Las diferentes propiedades de un metal en comparación con otro dependen en parte del tamaño de sus átomos y de las particularidades de su disposición espacial. En las siguientes secciones exploraremos las similitudes y diferencias de cuatro de las geometrías cristalinas más comunes de los metales.

Celdas unitarias de los metales

La estructura de un sólido cristalino, ya sea un metal o no, se describe mejor considerando su unidad de repetición más simple, que se denomina celda unitaria. La celda unitaria consiste en puntos de la red que representan las ubicaciones de los átomos o iones. La estructura completa está formada por esta celda unitaria que se repite en tres dimensiones, como se ilustra en la figura 1.

Se ofrecen dos dibujos. A la izquierda, se representa un cubo con puntos de red en cada esquina y células unitarias como lados. A la derecha, el mismo cubo se muestra replicado en letra gris, para mostrar una red infinita de cubos similares.

Figura 1. Una celda unitaria muestra las ubicaciones de los puntos de la red que se repiten en todas las direcciones.

Empecemos nuestra investigación sobre la estructura de la red cristalina y las celdas unitarias con la estructura más sencilla y la celda unitaria más básica. Para visualizarlo, imaginemos que tomamos un gran número de esferas idénticas, como pelotas de tenis, y las disponemos uniformemente en un recipiente. La forma más sencilla de hacerlo sería hacer capas en las que las esferas de una capa estén directamente encima de las de la capa inferior, como se ilustra en la figura 2. Esta disposición se denomina estructura cúbica simple, y la celda unitaria se llama celda unitaria cúbica simple o celda unitaria cúbica primitiva.

Tres dibujos del mismo cubo de 10.44. A la izquierda, se dibujan círculos alrededor de los puntos de la red. En el centro, estos círculos de los puntos de celosía se convierten en esferas marrones impuestas a la caja. A la derecha, vemos la misma representación de cajas infinitas que en 10.44.

Figura 2. Cuando los átomos de metal están dispuestos con esferas en una capa directamente encima o debajo de esferas en otra capa, la estructura de la red se llama cúbica simple. Obsérvese que las esferas están en contacto.

En una estructura cúbica simple, las esferas no están empaquetadas tan estrechamente como podrían estarlo, y sólo «llenan» alrededor del 52% del volumen del recipiente. Esta es una disposición relativamente ineficiente, y sólo un metal (el polonio, Po) cristaliza en una estructura cúbica simple. Como se muestra en la figura 3, un sólido con este tipo de disposición consta de planos (o capas) en los que cada átomo contacta sólo con los cuatro vecinos más cercanos de su capa; un átomo directamente por encima de él en la capa de arriba; y un átomo directamente por debajo en la capa de abajo. El número de otras partículas con las que contacta cada partícula de un sólido cristalino se conoce como su número de coordinación. Para un átomo de polonio en un conjunto cúbico simple, el número de coordinación es, por tanto, seis.

Se muestran dos dibujos. A la izquierda aparece la pila infinita de cubos de 10.44, esta vez sólo en blanco y negro. Se hace mucho hincapié en un punto de la red y en las líneas inmediatamente adyacentes a él en las aristas del cubo. A la derecha, aparece el mismo dibujo, esta vez con el punto de red en rojo y las líneas que irradian desde él etiquetadas como 1-6.

Figura 3. Un átomo en una estructura de red cúbica simple contacta con otros seis átomos, por lo que tiene un número de coordinación de seis.

En una red cúbica simple, la celda unitaria que se repite en todas las direcciones es un cubo definido por los centros de ocho átomos, como se muestra en la figura 4. Los átomos de las esquinas adyacentes de esta celda unidad están en contacto entre sí, por lo que la longitud de las aristas de esta celda es igual a dos radios atómicos, o a un diámetro atómico. Una celda unitaria cúbica contiene sólo las partes de estos átomos que están dentro de ella. Como un átomo en una esquina de una celda unitaria cúbica simple está contenido por un total de ocho celdas unitarias, sólo un octavo de ese átomo está dentro de una celda unitaria específica. Y puesto que cada celda unitaria cúbica simple tiene un átomo en cada una de sus ocho «esquinas», hay 8 veces \frac{1}{8}=1 átomo dentro de una celda unitaria cúbica simple.

Se muestran dos dibujos. A la izquierda, aparece la unidad cúbica de 10.45, con moléculas esféricas grises superpuestas sobre cada punto de la red, etiquetada como "celda cúbica simple de la red". A la derecha, etiquetada como "8 esquinas", está la misma unidad cúbica, mostrando sólo las porciones de las esferas de las moléculas que aparecerían dentro de esta unidad cúbica.

Figura 4. Una celda unitaria de celosía cúbica simple contiene un octavo de átomo en cada una de sus ocho esquinas, por lo que contiene un átomo en total.

Ejemplo 1: Cálculo del radio y la densidad atómica de los metales, parte 1

La longitud de arista de la celda unitaria del polonio alfa es de 336 pm.

  1. Determine el radio de un átomo de polonio.
  2. Determine la densidad del polonio alfa.
Muestre la solución

El polonio alfa cristaliza en una celda unitaria cúbica simple:

Un diagrama muestra un cubo con una octava parte de ocho esferas dentro del cubo, una sección en cada esquina. A lo largo de la parte inferior derecha del cubo hay dos flechas de doble terminación que se extienden cada una a lo largo de la mitad de la distancia total a través del cubo. Cada flecha está etiquetada como
  1. Dos átomos de Po adyacentes están en contacto entre sí, por lo que la longitud de la arista de esta celda es igual a dos radios atómicos de Po: l=2r. Por lo tanto, el radio de Po es r=\dfrac{l}{2}=\dfrac{text{336 pm}{2}=\text{168 pm}.
  2. La densidad viene dada por \text{densidad}=\dfrac{text{masa}{volumen}. La densidad del polonio se puede encontrar determinando la densidad de su celda unitaria (la masa contenida en una celda unitaria dividida por el volumen de la celda unitaria). Dado que una celda unitaria de Po contiene un octavo de un átomo de Po en cada una de sus ocho esquinas, una celda unitaria contiene un átomo de Po.

La masa de una celda unitaria de Po puede hallarse mediante:

{text{1 celda unitaria de Po}}veces {dfrac{text{1 átomo de Po}} {text{1 celda unitaria de Po}}veces {dfrac{text{1 mol de Po}}{6.022 veces {10}^{23}{ átomos de Po}} {veces {dfrac{208,998}{texto{1 mol de Po}}=3.47 veces {10}^-22}{text{g}

El volumen de una célula unitaria de Po puede hallarse mediante:

V={l}^{3}=(336 veces {10}^-10}{text{cm})}^{3}=3.79 veces {10}^-23}{texto{cm}}^{3}

(Nótese que la longitud del borde fue convertida de pm a cm para obtener las unidades de volumen habituales para la densidad.)

Por lo tanto, la densidad de \text{Po}=dfrac{3.471 veces {10}^{-22}{texto{g}}{3,79 veces {10}^{-23}{texto{cm}}^{3}={texto{9,16 g/cm}^{3}

Comprueba tu aprendizaje

La longitud del borde de la celda unitaria del níquel es de 0,3524 nm. La densidad del Ni es de 8,90 g/cm3. Cristaliza el níquel en una estructura cúbica simple? Explique.

Mostrar solución

No. Si el Ni fuera cúbico simple, su densidad vendría dada por:

{texto{1 átomo de Ni} {veces{dfrac{texto{1 mol de Ni}}{6.022 veces {10}^{23}{cubos de Ni}{58,693}{texto{1 mol de Ni}}=9,746 veces {10}^{-23}{texto{g}
V={l}^{3}=(3,524 veces {10}^-8}{texto{cm})}^{3}=4.376 veces {10}^-23}{texto{cm}^{3}

Entonces la densidad del Ni sería ={dfrac}{9,746}{10}^-23}{texto{g}{4,376}{10}^-23}{texto{cm}^{3}={texto{2.23 g/cm}^{3}

Como la densidad real del Ni no se aproxima a ésta, el Ni no forma una estructura cúbica simple.

La mayoría de los cristales metálicos presentan uno de los cuatro tipos principales de células unitarias. Por ahora, nos centraremos en las tres celdas unitarias cúbicas: el cúbico simple (que ya hemos visto), la celda unitaria cúbica centrada en el cuerpo y la celda unitaria cúbica centrada en la cara, todas ellas ilustradas en la figura 5. (Obsérvese que, en realidad, hay siete sistemas de red diferentes, algunos de los cuales tienen más de un tipo de red, para un total de 14 tipos diferentes de celdas unitarias. Dejamos las geometrías más complicadas para más adelante en este módulo.)

La primera fila de dibujos está etiquetada como "ubicaciones de puntos de celosía". Debajo de ella hay tres imágenes. A la izquierda está el cubo unitario simple con 6 puntos de celosía. En el centro hay un cubo unitario un poco más grande con un punto rojo en el centro. A la derecha hay una unidad cúbica aún mayor con 6 puntos rojos en su interior, dispuestos en dos filas diagonales de 3. La fila inferior de dibujos está etiquetada como "Celdas unitarias cúbicas". A la izquierda está la unidad cúbica simple con moléculas grises superpuestas. En el centro está el mismo dibujo, con una molécula roja centrada en la caja. A la derecha está el mismo dibujo, con seis moléculas rojas en 2 líneas diagonales dentro de la caja.

Figura 5. Las celdas unitarias cúbicas de los metales muestran (en las figuras superiores) las ubicaciones de los puntos de la red y (en las figuras inferiores) los átomos metálicos situados en la celda unitaria.

Algunos metales cristalizan en una disposición que tiene una celda unitaria cúbica con átomos en todas las esquinas y un átomo en el centro, como se muestra en la figura 6. Esto se llama un sólido cúbico centrado en el cuerpo (BCC). Los átomos de las esquinas de una celda unitaria BCC no están en contacto entre sí, sino con el átomo del centro. Una celda unitaria BCC contiene dos átomos: un octavo de átomo en cada una de las ocho esquinas (8 veces \frac{1}{8}=1 átomo de las esquinas) más un átomo del centro. Cualquier átomo de esta estructura toca cuatro átomos de la capa superior y cuatro átomos de la capa inferior. Así, un átomo en una estructura BCC tiene un número de coordinación de ocho.

Aparecen tres dibujos. A la izquierda está el mismo dibujo de una unidad cúbica con un punto rojo en el centro, de la figura 10.48. En el centro está el mismo cubo con moléculas grises superpuestas, con una molécula roja en el centro, como la fila inferior de la Figura 10.48. A la izquierda vemos las partes de las moléculas fuera del cubo raspadas, y sólo quedan trozos de las moléculas grises y la molécula roja entera.

Figura 6. En una estructura cúbica centrada en el cuerpo, los átomos de una determinada capa no se tocan entre sí. Cada átomo toca cuatro átomos de la capa superior y cuatro átomos de la capa inferior.

Los átomos en las disposiciones BCC se empaquetan de forma mucho más eficiente que en una estructura cúbica simple, ocupando aproximadamente el 68% del volumen total. Entre los metales isomorfos con estructura BCC se encuentran el K, el Ba, el Cr, el Mo, el W y el Fe a temperatura ambiente. (Se dice que los elementos o compuestos que cristalizan con la misma estructura son isomorfos.)

Muchos otros metales, como el aluminio, el cobre y el plomo, cristalizan en una disposición que tiene una celda unitaria cúbica con átomos en todas las esquinas y en los centros de cada cara, como se ilustra en la figura 7. Esta disposición se denomina sólido cúbico centrado en la cara (FCC). Una celda unitaria FCC contiene cuatro átomos: un octavo de un átomo en cada una de las ocho esquinas (8 veces \frac{1}{8}=1 átomo de las esquinas) y la mitad de un átomo en cada una de las seis caras (6 veces \frac{1}{2}=3 átomos de las caras). Los átomos de las esquinas tocan los átomos de los centros de las caras adyacentes a lo largo de las diagonales de las caras del cubo. Debido a que los átomos están en puntos idénticos de la red, tienen entornos idénticos.

Aparecen tres dibujos. A la izquierda está la misma unidad cúbica con 6 puntos rojos en su interior, como en la figura 10.48. En el centro está la misma unidad cúbica con moléculas esféricas superpuestas, como en la fila inferior de la figura 10.48. A la derecha, las moléculas grises que están fuera del cubo están raspadas, dejando sólo porciones de moléculas grises y seis mitades de moléculas rojas (ya que fueron divididas por la mitad).

Figura 7. Un sólido cúbico centrado en las caras tiene átomos en las esquinas y, como su nombre indica, en los centros de las caras de sus celdas unitarias.

Los átomos en una disposición FCC están empaquetados lo más cerca posible, con átomos que ocupan el 74% del volumen. Esta estructura también se denomina empaquetamiento cúbico más cercano (CCP). En el CCP, hay tres capas repetidas de átomos dispuestos de forma hexagonal. Cada átomo entra en contacto con seis átomos de su propia capa, tres de la capa superior y tres de la inferior. En esta disposición, cada átomo toca a 12 vecinos cercanos y, por tanto, tiene un número de coordinación de 12. El hecho de que las disposiciones FCC y CCP sean equivalentes puede no ser inmediatamente obvio, pero en la Figura 8 se ilustra por qué son realmente la misma estructura.

Se muestran tres imágenes. En la primera imagen, una vista lateral muestra una capa de esferas azules, etiquetadas como

Figura 8. Una disposición CCP consiste en tres capas repetidas (ABCABC…) de átomos dispuestos de forma hexagonal. Los átomos de una estructura CCP tienen un número de coordinación de 12 porque están en contacto con seis átomos de su capa, más tres átomos de la capa superior y tres átomos de la capa inferior. Girando nuestra perspectiva, podemos ver que una estructura CCP tiene una celda unidad con una cara que contiene un átomo de la capa A en una esquina, átomos de la capa B a través de una diagonal (en dos esquinas y en el centro de la cara), y un átomo de la capa C en la esquina restante. Esto es lo mismo que un arreglo cúbico centrado en la cara.

Debido a que el empaquetamiento más cercano maximiza las atracciones generales entre los átomos y minimiza la energía intermolecular total, los átomos en la mayoría de los metales se empaquetan de esta manera. Encontramos dos tipos de empaquetamiento más cercano en las estructuras cristalinas metálicas simples: El CCP, que ya hemos encontrado, y el empaquetamiento más cercano hexagonal (HCP) que se muestra en la figura 9. Ambos consisten en la repetición de capas de átomos dispuestos de forma hexagonal. En ambos tipos, una segunda capa (B) se coloca sobre la primera capa (A) de forma que cada átomo de la segunda capa está en contacto con tres átomos de la primera capa. La tercera capa se coloca de dos maneras. En HCP, los átomos de la tercera capa están directamente por encima de los átomos de la primera capa (es decir, la tercera capa también es de tipo A), y el apilamiento consiste en alternar capas de tipo A y de tipo B con empaquetamiento cerrado (es decir, ABABAB⋯). En el CCP, los átomos de la tercera capa no están por encima de los átomos de ninguna de las dos primeras capas (es decir, la tercera capa es de tipo C), y el apilamiento consiste en la alternancia de capas de tipo A, de tipo B y de tipo C (es decir, ABCABCABC⋯). Alrededor de dos tercios de todos los metales cristalizan en arreglos de paquetes cercanos con números de coordinación de 12. Los metales que cristalizan en una estructura HCP incluyen Cd, Co, Li, Mg, Na y Zn, y los metales que cristalizan en una estructura CCP incluyen Ag, Al, Ca, Cu, Ni, Pb y Pt.

Se muestran dos imágenes. La primera imagen, etiquetada como

Figura 9. En ambos tipos de empaquetamiento más cercano, los átomos se empaquetan de la forma más compacta posible. El empaquetamiento más cercano hexagonal consiste en dos capas alternas (ABABAB…). El empaquetamiento cúbico más cercano consiste en tres capas alternas (ABCABCABC…).

Ejemplo 2: Cálculo del radio y la densidad atómica de los metales, Parte 2

El calcio cristaliza en una estructura cúbica centrada en la cara. La longitud de la arista de su celda unitaria es de 558,8 pm.

  1. ¿Cuál es el radio atómico del Ca en esta estructura?
  2. Calcule la densidad del Ca.
Mostrar Solución

Parte 1

Se muestran dos dibujos. En el de la derecha, "hexagonal closest packed", vemos una vista lateral de 4 filas de esferas. La capa superior y la tercera son verdes, mientras que la segunda y la cuarta son azules. A la derecha, "cubic closest packed", vemos una vista lateral de cuatro filas de esferas. La fila superior e inferior son azules (la superior está etiquetada como capa C). La segunda fila es verde y se denomina capa B. La tercera fila es púrpura y se denomina capa A.

En una estructura FCC, los átomos de Ca están en contacto entre sí a través de la diagonal de la cara, por lo que la longitud de la diagonal es igual a cuatro radios atómicos de Ca (d = 4r). Dos bordes adyacentes y la diagonal de la cara forman un triángulo rectángulo, con la longitud de cada lado igual a 558,8 pm y la longitud de la hipotenusa igual a cuatro radios atómicos de Ca:

{text{a}^{2}+{text{a}^{2}={text{d}^{2}{longrightarrow {(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}={(4r)}^{2}

Solving this gives r=\sqrt{\dfrac{{(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}{16}}={text{197,6 pmg para un radio de Ca}.

Parte 2

La densidad viene dada por \text{densidad}={dfrac{text{masa}}{text{volumen}}. La densidad del calcio puede encontrarse determinando la densidad de su celda unitaria: por ejemplo, la masa contenida en una celda unitaria dividida por el volumen de la celda unitaria. Una celda unitaria de Ca centrada en una cara tiene un octavo de átomo en cada una de las ocho esquinas (8 veces dfrac{1}{8}=1\text{ átomo} {derecha) y la mitad de un átomo en cada una de las seis caras (6 veces dfrac{1}{2}=3\text{ átomos} {derecha), para un total de cuatro átomos en la celda unitaria.

La masa de la celda unitaria se puede encontrar por:

{célula unitaria de Ca} {veces dfrac {4 átomos de Ca} {célula unitaria de Ca} {veces dfrac {mol de Ca} {6.022 veces {10}^{23} {a átomos de Ca} {a veces {dfrac{40,078}{texto{1 mol de Ca}}=2.662 veces {10}^-22}{texto{g}}

El volumen de una célula unitaria de Ca puede hallarse mediante:

V={a}^{3}={(558,8 veces {10}^-10}{texto{cm})}^{3}=1.745 veces {10}^22}{text{cm}}^{3}

(Obsérvese que la longitud del borde se convirtió de pm a cm para obtener las unidades de volumen habituales para la densidad.)

Entonces, la densidad de \text{Ca}={dfrac{2,662} veces {10}^{-22}{text{g}}{1,745} veces {10}^{text{cm}}^{3}}={text{153 g/cm}^{3}

Comprueba tu aprendizaje

La plata cristaliza en una estructura FCC. La longitud del borde de su celda unitaria es de 409 pm.

  1. ¿Cuál es el radio atómico de la Ag en esta estructura?
  2. Calcule la densidad de la Ag.
Muestre las soluciones

  1. 144 pm
  2. 10.5 g/cm3

En general, una celda unitaria se define por las longitudes de tres ejes (a, b y c) y los ángulos (α, β y γ) entre ellos, como se ilustra en la figura 10. Los ejes se definen como las longitudes entre los puntos de la red espacial. En consecuencia, los ejes de la celda unidad unen puntos con entornos idénticos.

Se muestra un dibujo de una unidad cúbica, con puntos de la red. Los planos de la superficie del cubo están etiquetados como a, b y c. Alrededor de un punto de celosía aparece un círculo de flechas, etiquetado como (α, β y γ).

Figura 10. Una celda unitaria se define por las longitudes de sus tres ejes (a, b y c) y los ángulos (α, β y γ) entre los ejes.

Hay siete sistemas de entramado diferentes, algunos de los cuales tienen más de un tipo de entramado, para un total de catorce celdas unitarias diferentes, que tienen las formas mostradas en la Figura 11.

Una tabla de 7 filas, con dos columnas tituladas Sistema/Ejes/Angulos y Celdas Unitarias.

Figura 11. Hay siete sistemas de red diferentes y 14 celdas unitarias distintas.

Las estructuras de los cristales iónicos

Los cristales iónicos están formados por dos o más tipos diferentes de iones que suelen tener tamaños distintos. El empaquetamiento de estos iones en una estructura cristalina es más complejo que el empaquetamiento de átomos metálicos del mismo tamaño.

La mayoría de los iones monatómicos se comportan como esferas cargadas, y su atracción por los iones de carga opuesta es la misma en todas las direcciones. En consecuencia, las estructuras estables de los compuestos iónicos resultan (1) cuando los iones de una carga están rodeados por tantos iones como sea posible de la carga opuesta y (2) cuando los cationes y los aniones están en contacto entre sí. Las estructuras están determinadas por dos factores principales: los tamaños relativos de los iones y la relación entre el número de iones positivos y negativos en el compuesto.

Una imagen muestra una vista superior de una capa de esferas azules dispuestas en una lámina que se encuentra encima de otra lámina igual, excepto que las esferas son verdes. La segunda hoja está un poco desplazada, de modo que las esferas de la hoja superior se encuentran en las ranuras de la segunda hoja. En la parte inferior hay una tercera hoja compuesta por esferas de color morado. Los espacios creados entre las esferas de cada capa están etiquetados como

Figura 12. Los cationes pueden ocupar dos tipos de agujeros entre los aniones: agujeros octaédricos o agujeros tetraédricos.

En las estructuras iónicas sencillas, solemos encontrar los aniones, que normalmente son más grandes que los cationes, dispuestos en un conjunto lo más parecido posible. (Como se ha visto anteriormente, los electrones adicionales atraídos por el mismo núcleo hacen que los aniones sean más grandes y los electrones menos atraídos por el mismo núcleo hacen que los cationes sean más pequeños en comparación con los átomos de los que están formados). Los cationes más pequeños suelen ocupar uno de los dos tipos de huecos (o intersticios) que quedan entre los aniones. El más pequeño de los agujeros se encuentra entre tres aniones en un plano y un anión en un plano adyacente. Los cuatro aniones que rodean este agujero están dispuestos en las esquinas de un tetraedro, por lo que el agujero se denomina agujero tetraédrico. El tipo de agujero más grande se encuentra en el centro de seis aniones (tres en una capa y tres en una capa adyacente) situados en las esquinas de un octaedro; esto se denomina agujero octaédrico. La figura 12 ilustra ambos tipos de agujeros.

Dependiendo de los tamaños relativos de los cationes y aniones, los cationes de un compuesto iónico pueden ocupar agujeros tetraédricos u octaédricos, como se ilustra en la figura 13. Los cationes relativamente pequeños ocupan agujeros tetraédricos y los cationes más grandes ocupan agujeros octaédricos. Si los cationes son demasiado grandes para encajar en los agujeros octaédricos, los aniones pueden adoptar una estructura más abierta, como un simple conjunto cúbico. Los cationes más grandes pueden entonces ocupar los agujeros cúbicos más grandes que hace posible el espacio más abierto.

Se dan tres dibujos de cubos de celosía. A la izquierda, la unidad cúbica de abajo a la izquierda tiene puntos de celosía verdes, y todos los demás cubos los tienen morados (etiquetados como agujero tetraédrico). En el centro, los puntos de la red son verdes o naranjas, en una línea diagonal (etiquetada como agujero octaédrico). A la derecha, todos los puntos de la red son de color púrpura, etiquetados como agujero cúbico.

Figura 13. El tamaño de un catión y la forma del agujero ocupado por el compuesto están directamente relacionados.

Hay dos agujeros tetraédricos para cada anión en un conjunto de aniones HCP o CCP. Un compuesto que cristaliza en una matriz de aniones con los cationes en los agujeros tetraédricos puede tener una relación catión:anión máxima de 2:1; todos los agujeros tetraédricos se llenan en esta proporción. Algunos ejemplos son Li2O, Na2O, Li2S y Na2S. Los compuestos con una relación inferior a 2:1 también pueden cristalizar en un conjunto de aniones con cationes en los agujeros tetraédricos, si los tamaños iónicos encajan. En estos compuestos, sin embargo, algunos de los agujeros tetraédricos permanecen vacantes.

Ejemplo 3: Ocupación de los agujeros tetraédricos

El sulfuro de zinc es una importante fuente industrial de zinc y también se utiliza como pigmento blanco en la pintura. El sulfuro de zinc cristaliza con iones de zinc que ocupan la mitad de los agujeros tetraédricos en un conjunto de iones de sulfuro con el empaquetamiento más cercano. ¿Cuál es la fórmula del sulfuro de zinc?

Mostrar solución

Como hay dos agujeros tetraédricos por cada anión (ion sulfuro) y la mitad de estos agujeros están ocupados por iones de zinc, debe haber \frac{1}{2}{2} veces 2, o 1, ion de zinc por ion sulfuro. Por lo tanto, la fórmula es ZnS.

Comprueba tu aprendizaje

El seleniuro de litio puede describirse como un conjunto de iones de seleniuro con iones de litio en todos los agujeros tetraédricos. ¿Cuál es la fórmula del seleniuro de litio?

Mostrar solución

Li2Se

La proporción de agujeros octaédricos y aniones en una estructura HCP o CCP es de 1:1. Por lo tanto, los compuestos con cationes en agujeros octaédricos en un conjunto de aniones con el empaquetamiento más cercano pueden tener una relación catión:anión máxima de 1:1. En NiO, MnS, NaCl y KH, por ejemplo, todos los agujeros octaédricos están llenos. Se observan proporciones inferiores a 1:1 cuando algunos de los agujeros octaédricos permanecen vacíos.

Ejemplo 4: Estequiometría de los compuestos iónicos

El zafiro es óxido de aluminio. El óxido de aluminio cristaliza con iones de aluminio en dos tercios de los agujeros octaédricos en un conjunto de iones de óxido con el empaquetamiento más cercano. ¿Cuál es la fórmula del óxido de aluminio?

Mostrar solución

Debido a que hay un agujero octaédrico por cada anión (ion de óxido) y a que sólo dos tercios de estos agujeros están ocupados, la relación entre el aluminio y el oxígeno debe ser \frac{2}{3} :1, lo que daría {\text{Al}}_{2\text{/}}\frac{O}. La proporción de números enteros más sencilla es 2:3, por lo que la fórmula es Al2O3.

Comprueba tu aprendizaje

El pigmento blanco óxido de titanio cristaliza con iones de titanio en la mitad de los agujeros octaédricos de un conjunto de iones de óxido lo más empaquetado posible. ¿Cuál es la fórmula del óxido de titanio?

Mostrar solución

TiO2

En una matriz cúbica simple de aniones, hay un agujero cúbico que puede ser ocupado por un catión por cada anión en la matriz. En el CsCl, y en otros compuestos con la misma estructura, todos los agujeros cúbicos están ocupados. La mitad de los agujeros cúbicos están ocupados en el SrH2, UO2, SrCl2 y CaF2.

Diferentes tipos de compuestos iónicos a menudo cristalizan en la misma estructura cuando los tamaños relativos de sus iones y sus estequiometrías (las dos características principales que determinan la estructura) son similares.

Células unitarias de compuestos iónicos

Muchos compuestos iónicos cristalizan con células unitarias cúbicas, y utilizaremos estos compuestos para describir las características generales de las estructuras iónicas.

Cuando un compuesto iónico está formado por cationes y aniones de tamaño similar en una proporción 1:1, suele formar una estructura cúbica simple. El cloruro de cesio, CsCl, (ilustrado en la Figura 14) es un ejemplo de esto, con Cs+ y Cl- con radios de 174 pm y 181 pm, respectivamente. Podemos pensar en esto como si los iones de cloruro formaran una celda unitaria cúbica simple, con un ion de cesio en el centro; o como si los iones de cesio formaran una celda unitaria con un ion de cloruro en el centro; o como si las celdas unitarias cúbicas simples formadas por los iones Cs+ se superpusieran a las celdas unitarias formadas por los iones Cl-. Los iones de cesio y los iones de cloruro se tocan a lo largo de las diagonales del cuerpo de las celdas unitarias. Un ion cesio y un ion cloruro están presentes por celda unidad, dando la estequiometría l:l requerida por la fórmula del cloruro de cesio. Nótese que no hay ningún punto de red en el centro de la celda, y que CsCl no es una estructura BCC porque un ion cesio no es idéntico a un ion cloruro.

Se muestran tres dibujos. A la izquierda hay una representación de una unidad cúbica infinita, con el cubo inferior izquierdo que contiene un punto rojo en su centro. En el centro, aparece este único cubo, con los puntos de la red como grandes esferas moradas. La molécula central es más pequeña y verde. A la derecha, aparece un cubo apilado de esferas púrpuras, con pequeñas esferas verdes entre ellas mostrando un lado.

Figura 14. Los compuestos iónicos con cationes y aniones de tamaño similar, como el CsCl, suelen formar una estructura cúbica simple. Pueden describirse mediante celdas unitarias con cationes en las esquinas o aniones en las esquinas.

Hemos dicho que la ubicación de los puntos de la red es arbitraria. Esto se ilustra con una descripción alternativa de la estructura de CsCl en la que los puntos de red están situados en los centros de los iones de cesio. En esta descripción, los iones de cesio están situados en los puntos de la red en las esquinas de la celda, y el ion cloruro está situado en el centro de la celda. Las dos celdas unitarias son diferentes, pero describen estructuras idénticas.

Cuando un compuesto iónico está formado por una proporción 1:1 de cationes y aniones que difieren significativamente en tamaño, suele cristalizar con una celda unitaria FCC, como la que se muestra en la figura 15. El cloruro de sodio, NaCl, es un ejemplo de ello, ya que el Na+ y el Cl- tienen radios de 102 pm y 181 pm, respectivamente. Podemos pensar que los iones de cloruro forman una celda FCC, con los iones de sodio situados en los agujeros octaédricos en medio de los bordes de la celda y en el centro de la misma. Los iones de sodio y cloruro se tocan a lo largo de los bordes de la celda. La celda unidad contiene cuatro iones de sodio y cuatro iones de cloruro, dando la estequiometría 1:1 requerida por la fórmula, NaCl.

Se muestran tres imágenes. La primera imagen muestra un cubo con puntos negros en cada esquina y un punto rojo en el centro. Este cubo está apilado con otros siete que no están coloreados para formar un cubo más grande. La segunda imagen está compuesta por ocho esferas que se agrupan para formar un cubo con una esfera mucho más grande en el centro. El nombre bajo esta imagen dice

Figura 15. Los compuestos iónicos con aniones mucho más grandes que los cationes, como el NaCl, suelen formar una estructura FCC. Pueden describirse mediante celdas unitarias FCC con cationes en los huecos octaédricos.

La forma cúbica del sulfuro de zinc, la blenda de zinc, también cristaliza en una celda unitaria FCC, como se ilustra en la figura 16. Esta estructura contiene iones de sulfuro en los puntos de red de una red FCC. (La disposición de los iones de sulfuro es idéntica a la de los iones de cloruro en el cloruro de sodio). El radio de un ion de zinc es sólo un 40% del radio de un ion de sulfuro, por lo que estos pequeños iones Zn2+ están situados en agujeros tetraédricos alternos, es decir, en una mitad de los agujeros tetraédricos. Hay cuatro iones de zinc y cuatro iones de sulfuro en la celda unitaria, lo que da la fórmula empírica ZnS.

Aparecen dos dibujos. A la izquierda, se representa una estructura cúbica infinita, con el cubo inferior izquierdo que contiene seis puntos rojos. A la derecha, este cubo se amplía y aparecen puntos amarillos a intervalos aleatorios en los bordes y en el interior del cubo, para representar los puntos de la red.

Figura 16. ZnS, el sulfuro de zinc (o blenda de zinc) forma una celda unitaria FCC con iones de sulfuro en los puntos de la red y iones de zinc mucho más pequeños que ocupan la mitad de los agujeros tetraédricos de la estructura.

Una celda unitaria de fluoruro de calcio, como la que se muestra en la figura 17, es también una celda unitaria FCC, pero en este caso, los cationes están situados en los puntos de la red; los iones de calcio equivalentes están situados en los puntos de la red de una red FCC. Todos los sitios tetraédricos de la red FCC de iones de calcio están ocupados por iones de fluoruro. Hay cuatro iones de calcio y ocho iones de flúor en una celda unitaria, lo que da una relación calcio:flúor de l:2, tal y como requiere la fórmula química, CaF2. Un examen minucioso de la figura 17 revelará una simple matriz cúbica de iones de fluoruro con iones de calcio en una mitad de los huecos cúbicos. La estructura no puede describirse en términos de un entramado espacial de puntos en los iones de fluoruro porque los iones de fluoruro no tienen todos entornos idénticos. La orientación de los cuatro iones de calcio sobre los iones de flúor es diferente.

Aparecen dos dibujos. A la izquierda hay una representación de una estructura cúbica infinita, con el cubo inferior izquierdo que contiene seis puntos rojos. A la derecha, este único cubo se amplía para mostrar muchas esferas verdes, en las esquinas del cubo y en el interior. Todas están conectadas con líneas. Celda unitaria cara-centrada de CaF2 etiquetada.

Figura 17. El fluoruro de calcio, CaF2, forma una celda unitaria FCC con los iones de calcio (verde) en los puntos de la red y los iones de fluoruro (rojo) ocupando todos los sitios tetraédricos entre ellos.

Cálculo de los radios iónicos

Si conocemos la longitud de los bordes de una celda unitaria de un compuesto iónico y la posición de los iones en la celda, podemos calcular los radios iónicos de los iones del compuesto si hacemos suposiciones sobre las formas y los contactos iónicos individuales.

Ejemplo 5: Cálculo de radios iónicos

La longitud del borde de la celda unitaria del LiCl (estructura tipo NaCl, FCC) es de 0.514 nm o 5,14 Å. Suponiendo que el ion de litio es lo suficientemente pequeño como para que los iones de cloruro estén en contacto, como en la figura 15, calcule el radio iónico para el ion de cloruro.

Nota: La unidad de longitud angstrom, Å, se utiliza a menudo para representar dimensiones a escala atómica y equivale a 10-10 m.

Mostrar solución

En la cara de una celda unitaria de LiCl, los iones cloruro contactan entre sí a través de la diagonal de la cara:

Se muestran tres imágenes. La primera muestra un cubo de esferas alternas de color verde y púrpura. Se perfila un cubo más pequeño dentro de ese cubo y a continuación aparece una versión más grande del mismo. Esta figura es un cubo gris que parece estar formado por esferas. Hay pequeños espacios entre cada esfera. Hay un triángulo rectángulo delineado en este cubo y a continuación aparece una versión más grande del mismo. Este triángulo rectángulo tiene dos lados etiquetados

Dibujando un triángulo rectángulo en la cara de la celda unitaria, vemos que la longitud de la diagonal es igual a cuatro radios de cloruro (un radio desde cada cloruro de la esquina y un diámetro -que equivale a dos radios- desde el ion cloruro del centro de la cara), por lo que d = 4r. A partir del teorema de Pitágoras, tenemos:

{{texto{a}^{2}+{texto{a}^{2}={texto{d}^{2}

lo que da como resultado:

{Izquierda(0,514{texto{nm}{d})^{2}+{Izquierda(0.514\text{ nm}\right)^{2}={\left(4r\right)}^{2}=16{r}^{2}

Solving this gives:

r=\sqrt{\dfrac{{(0.514\text{nm})}^{2}+{(0.514\text{nm})}^{2}}{16}}=\text{0.182 nm} (1,82 Å) para un radio de Cl-

Comprueba tu aprendizaje

La longitud del borde de la celda unitaria de KCl (estructura tipo NaCl, FCC) es de 6,28 Å. Suponiendo un contacto anión-catión a lo largo del borde de la celda, calcula el radio del ion potasio. El radio del ion cloruro es de 1,82 Å.

Mostrar solución

El radio del ion potasio es de 1,33 Å.

Es importante darse cuenta de que los valores de los radios iónicos calculados a partir de las longitudes de los bordes de las celdas unitarias dependen de numerosas suposiciones, como una forma esférica perfecta para los iones, que son aproximaciones en el mejor de los casos. Por lo tanto, estos valores calculados son en sí mismos aproximados y las comparaciones no pueden llevarse demasiado lejos. No obstante, este método ha demostrado ser útil para calcular los radios iónicos a partir de mediciones experimentales como las determinaciones cristalográficas de rayos X.

Cristalografía de rayos X

El tamaño de la celda unitaria y la disposición de los átomos en un cristal pueden determinarse a partir de mediciones de la difracción de los rayos X por el cristal, lo que se denomina cristalografía de rayos X. La difracción es el cambio de dirección que experimenta una onda electromagnética cuando encuentra una barrera física cuyas dimensiones son comparables a las de la longitud de onda de la luz. Los rayos X son radiaciones electromagnéticas con longitudes de onda aproximadamente tan largas como la distancia entre los átomos vecinos en los cristales (del orden de unos pocos Å).

Cuando un haz de rayos X monocromáticos incide en un cristal, sus rayos son dispersados en todas las direcciones por los átomos dentro del cristal. Cuando las ondas dispersas que viajan en la misma dirección se encuentran entre sí, sufren interferencia, un proceso por el cual las ondas se combinan para producir un aumento o una disminución de la amplitud (intensidad), dependiendo de la medida en que los máximos de las ondas combinadas estén separados (véase la figura 18).

Se muestra un par de imágenes que tiene cuatro secciones. En la primera sección, se muestran dos ondas sinusoidales, una dibujada encima de la otra, y se marca una sección desde la parte superior de una curva hasta la parte superior de la siguiente curva

Figura 18. Las ondas luminosas que ocupan el mismo espacio experimentan interferencia, combinándose para dar lugar a ondas de mayor (a) o menor (b) intensidad, dependiendo de la separación de sus máximos y mínimos.

Cuando los rayos X de una determinada longitud de onda, λ, son dispersados por átomos en planos cristalinos adyacentes separados por una distancia, d, pueden sufrir interferencia constructiva cuando la diferencia entre las distancias recorridas por las dos ondas antes de su combinación es un factor entero, n, de la longitud de onda. Esta condición se satisface cuando el ángulo del haz difractado, θ, se relaciona con la longitud de onda y la distancia interatómica mediante la ecuación:

n{lambda}=2d{text{sin}\theta

Esta relación se conoce como ecuación de Bragg en honor a W. H. Bragg, el físico inglés que explicó por primera vez este fenómeno. La figura 19 ilustra dos ejemplos de ondas difractadas desde los mismos dos planos de cristal. La figura de la izquierda representa las ondas difractadas en el ángulo de Bragg, dando lugar a una interferencia constructiva, mientras que la de la derecha muestra la difracción y un ángulo diferente que no satisface la condición de Bragg, dando lugar a una interferencia destructiva.

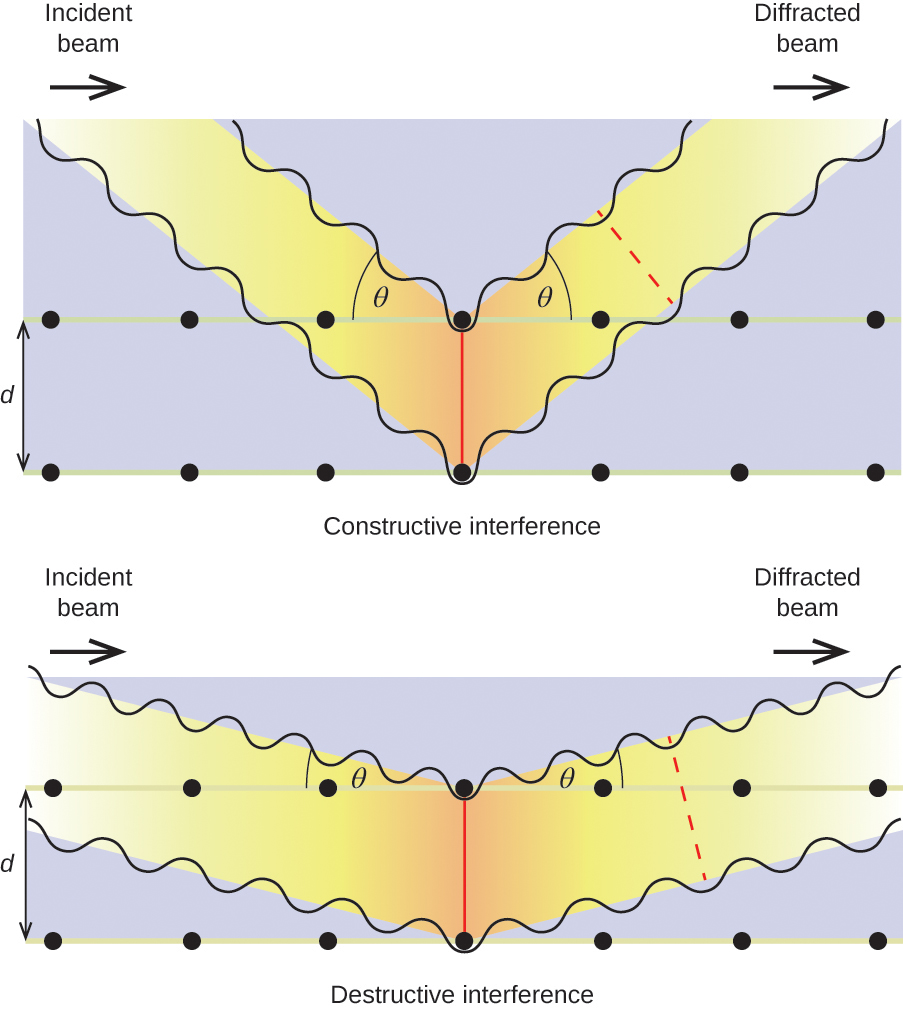
Se muestran dos figuras similares. La primera figura, etiquetada como

Figura 19. La difracción de los rayos X dispersados por los átomos dentro de un cristal permite determinar la distancia entre los átomos. La imagen superior muestra la interferencia constructiva entre dos ondas dispersas y una onda difractada resultante de alta intensidad. La imagen inferior muestra la interferencia destructiva y una onda difractada de baja intensidad.

Visite «¿Qué es la ley de Bragg y por qué es importante?» para obtener más detalles sobre la ecuación de Bragg y un simulador que le permite explorar el efecto de cada variable sobre la intensidad de la onda difractada.

Un difractómetro de rayos X, como el que se ilustra en la Figura 20, puede utilizarse para medir los ángulos a los que se difractan los rayos X cuando interactúan con un cristal como se ha descrito anteriormente. A partir de estas mediciones, la ecuación de Bragg puede utilizarse para calcular las distancias entre los átomos, como se demuestra en el siguiente ejercicio de ejemplo.

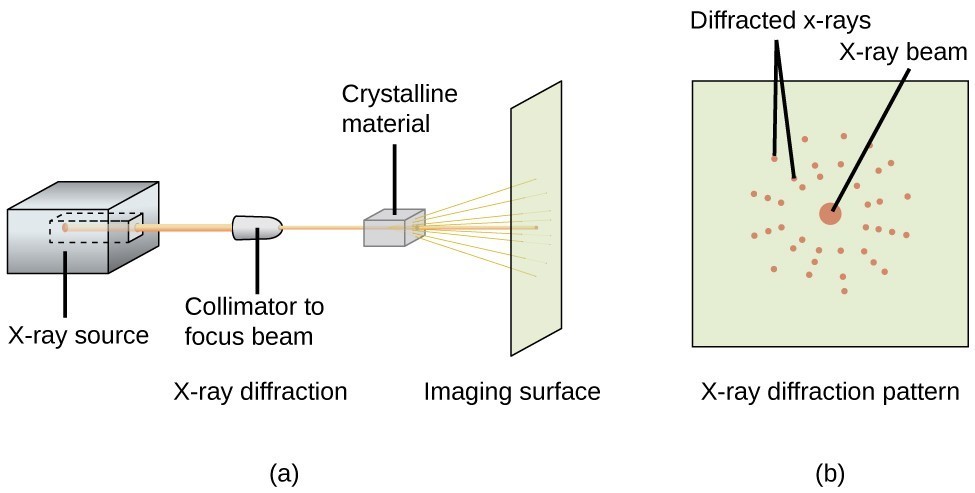
Se dan dos conjuntos de dibujos. A la derecha, a) es una vista lateral de una proyección de rayos X desde una máquina a la pared, pasando a través de material cristalino. A la derecha, b) es una imagen frontal de la pared, mostrando el haz de rayos X y los rayos X difractados que resultan.

Figura 20. En un difractómetro (a), un haz de rayos X incide sobre un material cristalino, produciendo un patrón de difracción de rayos X (b) que puede ser analizado para determinar la estructura cristalina.

Puede ver la transcripción de «Celebrando la Cristalografía – Una aventura animada» aquí (se abre en una nueva ventana).

Ejemplo 6: Uso de la ecuación de Bragg

En un difractómetro, se utilizaron rayos X con una longitud de onda de 0,1315 nm para producir un patrón de difracción para el cobre. La difracción de primer orden (n = 1) se produjo con un ángulo θ = 25,25°. Determine el espaciamiento entre los planos difractantes en el cobre.

Mostrar Solución

La distancia entre los planos se encuentra resolviendo la ecuación de Bragg, nλ = 2d sin θ, para d.

Esto da: d=\dfrac{n\lambda}{2\sin\theta}=\dfrac{1\\año(0.1315{text{nm}{derecho})}{2{sin{izquierda}(25,25^{circ}{derecho})}=0,154{text{nm}

Comprueba tu aprendizaje

Un cristal con separación entre planos igual a 0,394 nm difracta rayos X con una longitud de onda de 0,147 nm. ¿Cuál es el ángulo de difracción de primer orden?

Mostrar solución

10,8°

Retrato de una química: La cristalógrafa de rayos X Rosalind Franklin

Una imagen muestra una ilustración circular con anillos de puntos que se difuminan entre sí.

Figura 21. Esta ilustración muestra una imagen de difracción de rayos X similar a la que Franklin encontró en su investigación. (crédito: National Institutes of Health)

El descubrimiento de la estructura del ADN en 1953 por Francis Crick y James Watson es uno de los grandes logros de la historia de la ciencia. Fueron galardonados con el Premio Nobel de Fisiología o Medicina en 1962, junto con Maurice Wilkins, que aportó la prueba experimental de la estructura del ADN. La química británica Rosalind Franklin hizo una contribución inestimable a este monumental logro gracias a su trabajo de medición de imágenes de difracción de rayos X del ADN. Al principio de su carrera, las investigaciones de Franklin sobre la estructura del carbón fueron útiles para el esfuerzo bélico británico. A principios de la década de 1950, Franklin y su estudiante de doctorado Raymond Gosling descubrieron que el ADN tiene dos formas: una fibra larga y fina que se forma cuando está húmeda (tipo «B») y una fibra corta y ancha que se forma cuando se seca (tipo «A»). Sus imágenes de difracción de rayos X del ADN (Figura 21) proporcionaron la información crucial que permitió a Watson y Crick confirmar que el ADN forma una doble hélice y determinar los detalles de su tamaño y estructura.

Franklin también llevó a cabo una investigación pionera sobre los virus y el ARN que contiene su información genética, descubriendo nueva información que cambió radicalmente el conjunto de conocimientos en este campo. Tras desarrollar un cáncer de ovario, Franklin siguió trabajando hasta su muerte en 1958, a los 37 años. Entre los muchos reconocimientos póstumos a su trabajo, la Facultad de Medicina de Chicago de la Universidad Finch de Ciencias de la Salud cambió su nombre por el de Universidad Rosalind Franklin de Medicina y Ciencia en 2004, y adoptó una imagen de su famosa imagen de difracción de rayos X del ADN como logotipo oficial de la universidad.

Conceptos clave y resumen

Las estructuras de los metales cristalinos y los compuestos iónicos simples pueden describirse en términos de empaquetamiento de esferas. Los átomos metálicos pueden empaquetarse en estructuras hexagonales de empaquetamiento más cercano, estructuras cúbicas de empaquetamiento más cercano, estructuras centradas en el cuerpo y estructuras cúbicas simples. Los aniones de las estructuras iónicas simples suelen adoptar una de estas estructuras y los cationes ocupan los espacios que quedan entre los aniones. Los cationes pequeños suelen ocupar huecos tetraédricos en un conjunto de aniones lo más cercano posible. Los cationes más grandes suelen ocupar agujeros octaédricos. Los cationes más grandes pueden ocupar agujeros cúbicos en un conjunto cúbico simple de aniones. La estructura de un sólido puede describirse indicando el tamaño y la forma de una celda unitaria y el contenido de la misma. El tipo de estructura y las dimensiones de la celda unitaria pueden determinarse mediante mediciones de difracción de rayos X.

Ecuaciones clave

  • n{lambda}=2d{texto{sin} {theta

Inténtalo

  1. Describe la estructura cristalina del hierro, que cristaliza con dos átomos metálicos equivalentes en una celda unitaria cúbica.
  2. Describa la estructura cristalina del Pt, que cristaliza con cuatro átomos metálicos equivalentes en una celda unitaria cúbica.
  3. ¿Cuál es el número de coordinación de un átomo de cromo en la estructura cúbica centrada en el cuerpo del cromo?
  4. ¿Cuál es el número de coordinación de un átomo de aluminio en la estructura cúbica centrada en la cara del aluminio?
  5. El metal cobalto cristaliza en una estructura hexagonal de empaquetamiento más cercano. ¿Cuál es el número de coordinación de un átomo de cobalto?
  6. El níquel metálico cristaliza en una estructura cúbica de máximo empaquetamiento. ¿Cuál es el número de coordinación de un átomo de níquel?
  7. El tungsteno cristaliza en una celda unitaria cúbica centrada en el cuerpo con una longitud de arista de 3,165 Å.
    1. ¿Cuál es el radio atómico del tungsteno en esta estructura?
    2. Calcule la densidad del tungsteno.
  8. El platino (radio atómico = 1,38 Å) cristaliza en una estructura cúbica de empaquetamiento estrecho. Calcule la longitud de arista de la celda unitaria cúbica centrada en la cara y la densidad del platino.
  9. El bario cristaliza en una celda unitaria cúbica centrada en el cuerpo con una longitud de arista de 5.025 Å
    1. ¿Cuál es el radio atómico del bario en esta estructura?
    2. Calcule la densidad del bario.
  10. El aluminio (radio atómico = 1,43 Å) cristaliza en una estructura cúbica muy empaquetada. Calcule la longitud de la arista de la celda unitaria cúbica centrada en la cara y la densidad del aluminio.
  11. La densidad del aluminio es de 2,7 g/cm3; la del silicio es de 2,3 g/cm3. Explique por qué el Si tiene la densidad más baja a pesar de tener átomos más pesados.
  12. El espacio libre en un metal se puede encontrar restando el volumen de los átomos en una celda unitaria del volumen de la celda. Calcula el porcentaje de espacio libre en cada una de las tres celdas cúbicas si todos los átomos de cada una tienen el mismo tamaño y tocan a sus vecinos más cercanos. ¿Cuál de estas estructuras representa el empaquetamiento más eficiente? Es decir, ¿cuál empaqueta con la menor cantidad de espacio no utilizado?
  13. El sulfuro de cadmio, a veces utilizado como pigmento amarillo por los artistas, cristaliza con cadmio, ocupando la mitad de los agujeros tetraédricos en un conjunto de iones de sulfuro con el empaquetamiento más cercano. ¿Cuál es la fórmula del sulfuro de cadmio? Explique su respuesta.
  14. Un compuesto de cadmio, estaño y fósforo se utiliza en la fabricación de algunos semiconductores. Cristaliza con el cadmio ocupando una cuarta parte de los agujeros tetraédricos y el estaño ocupando una cuarta parte de los agujeros tetraédricos en un conjunto de iones de fosfuro muy empaquetado. Cuál es la fórmula del compuesto? Explique su respuesta.
  15. ¿Cuál es la fórmula del óxido magnético de cobalto, utilizado en las cintas de grabación, que cristaliza con átomos de cobalto ocupando un octavo de los agujeros tetraédricos y la mitad de los agujeros octaédricos en una matriz de iones de óxido estrechamente empaquetada?
  16. Un compuesto que contiene zinc, aluminio y azufre cristaliza con una matriz de iones de sulfuro estrechamente empaquetada. Los iones de zinc se encuentran en un octavo de los agujeros tetraédricos y los iones de aluminio en la mitad de los agujeros octaédricos. ¿Cuál es la fórmula empírica del compuesto?
  17. Un compuesto de talio y yodo cristaliza en una matriz cúbica simple de iones de yoduro con iones de talio en todos los agujeros cúbicos. ¿Cuál es la fórmula de este yoduro? Explique su respuesta.
  18. ¿Cuál de los siguientes elementos reacciona con el azufre para formar un sólido en el que los átomos de azufre forman un conjunto lo más parecido posible con todos los agujeros octaédricos ocupados: Li, Na, Be, Ca o Al?
  19. ¿Cuál es el porcentaje en masa de titanio en el rutilo, un mineral que contiene titanio y oxígeno, si la estructura puede describirse como un conjunto de iones de óxido con iones de titanio en la mitad de los agujeros octaédricos? ¿Cuál es el número de oxidación del titanio?
  20. Explique por qué los cloruros de metales alcalinos NaCl y CsCl, químicamente similares, tienen estructuras diferentes, mientras que el NaCl y el MnS, químicamente diferentes, tienen la misma estructura.
  21. Al formarse los minerales a partir del magma fundido, diferentes iones ocuparon los mismos cites en los cristales. El litio suele aparecer junto con el magnesio en los minerales a pesar de la diferencia de carga de sus iones. Sugiera una explicación.
  22. El yoduro de rubidio cristaliza con una celda unitaria cúbica que contiene iones de yoduro en las esquinas y un ion de rubidio en el centro. ¿Cuál es la fórmula del compuesto?
  23. Uno de los diversos óxidos de manganeso cristaliza con una celda unitaria cúbica que contiene iones de manganeso en las esquinas y en el centro. Los iones de óxido se encuentran en el centro de cada arista de la celda unitaria. ¿Cuál es la fórmula del compuesto?
  24. El NaH cristaliza con la misma estructura cristalina que el NaCl. La longitud de arista de la celda unitaria cúbica del NaH es de 4,880 Å.
    1. Calcule el radio iónico del H-. (El radio iónico del Li+ es 0,0,95 Å.)
    2. Calcule la densidad del NaH.
  25. El yoduro de Talio(I) cristaliza con la misma estructura que el CsCl. La longitud del borde de la celda unitaria del TlI es de 4,20 Å.
    1. Calcule el radio iónico del TI+. (El radio iónico del I- es de 2,16 Å.)
    2. Calcule la densidad del TlI.
  26. Una celda unitaria cúbica contiene iones de manganeso en las esquinas e iones de fluoruro en el centro de cada arista.
    1. ¿Cuál es la fórmula empírica de este compuesto? Explique su respuesta.
    2. ¿Cuál es el número de coordinación del ion Mn3+?
    3. Calcule la longitud del borde de la celda unitaria si el radio de un ion Mn3+ es de 0,65 A.
    4. Calcule la densidad del compuesto.
  27. ¿Cuál es el espaciamiento entre los planos del cristal que difractan rayos X con una longitud de onda de 1,541 nm a un ángulo θ de 15,55° (reflexión de primer orden)?
  28. Un difractómetro que utiliza rayos X con una longitud de onda de 0,2287 nm produce un pico de difracción de primer orden para un ángulo del cristal θ = 16,21°. Determine el espaciamiento entre los planos difractantes en este cristal.
  29. Un metal con espaciamiento entre planos igual a 0,4164 nm difracta rayos X con una longitud de onda de 0,2879 nm. ¿Cuál es el ángulo de difracción para el pico de difracción de primer orden?
  30. El oro cristaliza en una celda unitaria cúbica centrada en la cara. La reflexión de segundo orden (n = 2) de los rayos X para los planos que conforman las partes superior e inferior de las celdas unitarias está en θ = 22,20°. La longitud de onda de los rayos X es de 1,54 Å. ¿Cuál es la densidad del oro metálico?
  31. Cuando un electrón de un átomo excitado de molibdeno cae de la capa L a la K, se emite un rayo X. Estos rayos X se difractan en un ángulo de 7,75° por planos con una separación de 2,64 Å. ¿Cuál es la diferencia de energía entre la capa K y la capa L en el molibdeno suponiendo una difracción de primer orden?
Mostrar soluciones seleccionadas

1. La estructura de esta forma de hierro de baja temperatura (por debajo de 910 °C) es cúbica centrada en el cuerpo. Hay un octavo átomo en cada una de las ocho esquinas del cubo y un átomo en el centro del cubo.

3. El número de coordinación se refiere al número de vecinos más cercanos. Un átomo de cromo se encuentra en el centro de un cubo centrado en el cuerpo y tiene ocho vecinos más cercanos (en las esquinas del cubo): cuatro en un plano superior y cuatro en un plano inferior. El número de coordinación es, por tanto, ocho.

5. El empaquetamiento hexagonal más cercano se produce de forma que cada átomo toca a 12 vecinos más cercanos: 6 en su propia capa y 3 en cada capa adyacente. El número de coordinación es, por tanto, 12.

7. (a) En una celda unitaria cúbica centrada en el cuerpo, los átomos metálicos están en contacto a lo largo de la diagonal interior del cubo. La diagonal interior forma un triángulo rectángulo con la arista de la celda unidad y la diagonal de la cara. Utilice el teorema de Pitágoras para determinar la longitud de la diagonal, d, en la cara del cubo en términos de la arista, e.

d2 = e2 + e2 = 2e2

d = \sqrt{2} e

La diagonal interior del cubo es la longitud de cuatro radios atómicos y se puede calcular de nuevo utilizando el teorema de Pitágoras y la diagonal de la cara y la arista.

{comenzar{array}{rll} {Izquierda(\texto{diagonal}{derecha)^2&=&d^2+e^2 \\\N-&=& {Izquierda(\cuadrado{2} e\N-derecha)+e^2 \N-{5838>=& 2e^2+e^2 \N-{5838>=&3e^2 \text{diagonal}&=&\sqrt{3}e=4r{end{array}

radio del tungsteno = \frac{text{diagonal}{4}=\frac{sqrt{3}e}{4}=\frac{sqrt{3}{4}left(3.165mathring{{text{A}}right)=1,370mathring{{text{A}};

(b) Dada la estructura cúbica centrada en el cuerpo, cada celda unitaria contiene dos átomos. Utilice la longitud de la arista de la celda unitaria para calcular el volumen de la celda unitaria y el volumen ocupado por cada átomo. Multiplique para obtener el volumen molar y divida la masa atómica por este valor para obtener la densidad (e = longitud de arista):

V(celda) = e3 = (3,165 \times 10-8 cm)3 = 3,170 \times 10-23 cm3

V(átomo) = \frac{3,170\times {10}^{-23}{texto{cm}}^{3}{texto{2 átomos}}=1.585 veces {10}^23}{texto{cm}}^3}{texto{átomo}}^{-1}

V(mol) = 1,585 veces 10-23 cm3/átomo \Na 6,022 veces 1023 átomos/mol

= 9.546 cm3/mol

densidad = \frac{183,85{texto{g mol}^{-1}}{9,546{texto{cm}^{3}{texto{mol}^{-1}} = 19,26 g/cm

9. (a) En una celda unitaria cúbica centrada en el cuerpo, los átomos metálicos están en contacto a lo largo de la diagonal del cubo. La diagonal del cubo forma un triángulo rectángulo con la arista de la celda unitaria y la diagonal de una cara. Utilice el teorema de Pitágoras para determinar la longitud de la diagonal, d, en la cara del cubo en términos de e.

d2 = e2 + e2 = 2e2

d = \sqrt{2} e

La diagonal del cubo es la longitud de cuatro radios atómicos y se puede calcular utilizando de nuevo el teorema de Pitágoras:

(diagonal)2 = (4r)2 = (2e)2 + e2 = 16r2 = 3e2

diagonal = 4r = \sqrt{3\text{e}

r = \frac{sqrt{3}{4}text{e}=\frac{sqrt{3}{4} (5,025 Å) = 2,176 Å;

(b) Dada una estructura cúbica centrada en el cuerpo, cada celda unitaria contiene dos átomos. Utilice la longitud de la arista de la celda unitaria para calcular el volumen de la celda unitaria y el volumen ocupado por cada átomo. Multiplique para obtener el volumen molar y divida el peso atómico en gramos por este valor para obtener la densidad (e = longitud de arista):

V (celda) = e3 = (5,025 \times 10-8 cm)3 = 1,26884 \times 10-22 cm3

V (átomo) = 1.26884 \times \frac{10}^{-22}{text{cm}}^{3}{text{atom}}^{text{-1}} {{2 átomos}} = 6,3442 \times 10-23 cm3

V (mol) = 6.3442 \times 10-23 cm3 \times 6,022 \times 1023 átomos/mol = 38,205 cm3

d(Ba) = \frac{137,33 g}{38,204 cm}^{3} = 3,595 g/cm3

11. La estructura cristalina del Si muestra que está menos empaquetado (número de coordinación 4) en el sólido que el Al (número de coordinación 12).

13. En un conjunto de empaquetamiento más estrecho, existen dos agujeros tetraédricos por cada anión. Si sólo la mitad de los agujeros tetraédricos están ocupados, los números de aniones y cationes son iguales. La fórmula del sulfuro de cadmio es CdS.

15. En un conjunto de iones de óxido con el empaquetamiento más cercano, existe un agujero octaédrico y dos agujeros tetraédricos por cada ion de óxido. Si la mitad de los agujeros octaédricos están llenos, hay un ion de Co por cada dos iones de óxido. Si se llena un octavo de los agujeros tetraédricos, hay un ion Co por cada cuatro iones de óxido. Por cada cuatro iones de óxido, hay dos iones de Co en agujeros octaédricos y un Co en un agujero tetraédrico; por lo tanto, la fórmula es Co3O4.

17. En una matriz cúbica simple, sólo un agujero cúbico puede ser ocupado por un catión para cada anión en la matriz. La relación entre el talio y el yoduro debe ser de 1:1; por lo tanto, la fórmula del talio es TlI.

19. La relación entre los agujeros octaédricos y los aniones de oxígeno es de 1:1 en un conjunto con el empaquetamiento más cercano. Sólo la mitad de los agujeros octaédricos están ocupados. Por lo tanto, la relación entre el titanio y el oxígeno es de 1:2 y la fórmula es TiO2. El porcentaje en masa de Ti en la estructura es:

porcentaje de Ti = \frac{47,90}{47,90+\text{2(15,9994)}}=texto{100%}

El número de oxidación del titanio es +4 porque hay dos iones O2- por cada ion Ti.

21. Ambos iones tienen un tamaño cercano: Mg, 0,65; Li, 0,60. Esta similitud permite que ambos se intercambien con bastante facilidad. La diferencia de carga se compensa generalmente por el cambio de Si4+ por Al3+.

23. El número total de iones Mn se determina sumando las contribuciones de las esquinas y del centro. Mn (esquinas): 8 \N veces \frac{1}{8}; Mn (centro) = 1. Contribución total del Mn a la celda unitaria = 2.

Para el O, hay un total de 12 aristas en el cubo y cada ion en la arista contribuye un cuarto a la celda unitaria. Por lo tanto, hay 12 \Nveces \frac{1}{4} = 3 átomos de O. La relación es Mn:O = 2:3, y la fórmula es Mn2O3.

27. La ecuación de Bragg es: nλ = 2d sin θ

donde d es el espaciamiento entre planos.

d = \frac{n{lambda}}{text{2 sin}{theta}=\frac{1(1.541 A)}{2sin15,55^{circ}}=frac{1,541{mathring{{text{A}}{2(0,2681)} = 2,874 Å

29. \text{sin}\theta =\frac{n{lambda}}{2d}=\frac{1)(0,2879\text{nm})}{(2)(0,4164)}=0,3457, por lo que θ = sin-1(0,3457) = 20,2°

31. Utilice la ecuación de Bragg, donde n = 1,

λ = 2dsinθ =2(2,64 Å)sen 7,75 = 0,712 Å

Entonces E=\frac{hc}{lambda}=\frac{(6.626 veces {10}^-34} {texto{J})(2,998 veces {10}^8} {texto{m}}^{-1})}{0,712 veces {10}^-10} {texto{m}} =2,79 veces {10}^-15} {texto{J}=1.74 veces {10}^4}\texto{eV}

Glosario

Sólido cúbico centrado en el cuerpo (BCC): estructura cristalina que tiene una celda unitaria cúbica con puntos de red en las esquinas y en el centro de la celda

Cubo centrado en el cuerpo: unidad de repetición más simple de un cristal cúbico centrado en el cuerpo; es un cubo que contiene puntos de red en cada esquina y en el centro del cubo

Ecuación de Bragg: ecuación que relaciona los ángulos en los que los rayos X son difractados por los átomos dentro de un cristal

número de coordinación: número de átomos más cercanos a cualquier átomo dado en un cristal o al átomo de metal central en un complejo

empacamiento cúbico más cercano (CCP): estructura cristalina en la que los planos de átomos o iones estrechamente empaquetados se apilan como una serie de tres capas alternas de diferentes orientaciones relativas (ABC)

difracción: redirección de la radiación electromagnética que se produce cuando encuentra una barrera física de dimensiones adecuadas

sólido cúbico centrado en la cara (FCC): estructura cristalina formada por una celda unitaria cúbica con puntos de red en las esquinas y en el centro de cada cara

celda unitaria cúbica centrada en la cara: unidad de repetición más simple de un cristal cúbico centrado en la cara; es un cubo que contiene puntos de red en cada esquina y en el centro de cada cara

empaquetamiento hexagonal más cercano (HCP): estructura cristalina en la que las capas de átomos o iones estrechamente empaquetados se apilan como una serie de dos capas alternas de diferentes orientaciones relativas (AB)

agujero: (también, intersticio) espacio entre átomos dentro de un cristal

isomorfo: que posee la misma estructura cristalina

agujero octaédrico: espacio abierto en un cristal en el centro de seis partículas situadas en las esquinas de un octaedro

célula unitaria cúbica simple: (también, celda unitaria cúbica primitiva) celda unitaria en la estructura cúbica simple

estructura cúbica simple: estructura cristalina con una celda unitaria cúbica con puntos de entramado sólo en las esquinas

espacio de entramado: todos los puntos dentro de un cristal que tienen entornos idénticos

agujero tetraédrico: espacio tetraédrico formado por cuatro átomos o iones en un cristal

célula unitaria: porción más pequeña de una red espacial que se repite en tres dimensiones para formar toda la red

Cristalografía de rayos X: técnica experimental para determinar las distancias entre los átomos de un cristal midiendo los ángulos con los que se difractan los rayos X al atravesar el cristal

Articles