>

Um triplo pitagórico é um triplo de inteiros positivos , , e de tal forma que exista um triângulo direito com pernas e hipotenusa . Pelo teorema de Pitágoras, isto é equivalente a encontrar inteiros positivos , , e satisfazendo

O menor e mais conhecido triplo de Pitágoras é . O triângulo direito com estes comprimentos laterais é às vezes chamado de triângulo 3, 4, 5.

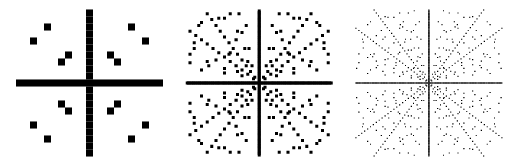
Lotes de pontos em -plano tal que é um triângulo pitágorico são mostrados acima para limites sucessivamente maiores. Estes gráficos incluem valores negativos de e , e são portanto simétricos em relação aos eixos x e y.

Similiarmente, gráficos de pontos no plano de tal forma que é um triplo pitágorico são mostrados acima para limites sucessivamente maiores.

>

É usual considerar apenas triplos pitagóricos primitivos (também chamados triplos “reduzidos”) nos quais e são relativamente primitivos, uma vez que outras soluções podem ser geradas trivialmente a partir dos primitivos. Os triplos primitivos são ilustrados acima, e pode-se ver imediatamente que as linhas radiais correspondentes aos triplos imprimitivos na trama original estão ausentes nesta figura. Para soluções primitivas, uma de ou deve ser par, e a outra ímpar (Shanks 1993, p. 141), com sempre ímpar.

Além disso, um lado de cada triplo de Pitágoras é divisível por 3, outro por 4, e outro por 5. Um lado pode ter dois destes divisores, como em (8, 15, 17), (7, 24, 25), e (20, 21, 29), ou mesmo os três, como em (11, 60, 61).

Dado um triplo primitivo , três novos triplos primitivos são obtidos de

			(2)
>			(3)
			(4)

where

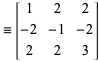		(5)
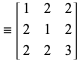		(6)
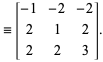		(7)

Hall (1970) e Roberts (1977) provam que é um triplo pitagórico primitivo iff

where é um produto finito das matrizes , , . Segue-se que cada triplo primitivo pitagórico deve ser um membro da matriz infinita

Pythagoras e os babilônios deram uma fórmula para gerar (não necessariamente primitivos) triplos como

para , o que gera um conjunto de triplos distintos contendo nem todos os triplos primitivos nem todos os triplos imprimitivos (e onde no caso especial , ).

Os primeiros gregos deram

onde e são relativamente primitivos e de paridade oposta (Shanks 1993, p. 141), que gera um conjunto de triplos distintos contendo precisamente os triplos primitivos (após a ordenação apropriada e ).

Let ser um número de Fibonacci. Então

genera triplos pitagóricos distintos (Dujella 1995), embora não exaustivamente para triplos primitivos ou imprimitivos. Mais genericamente, começando com inteiros positivos , , e construindo a sequência do tipo Fibonacci com termos , , , , , … gera triplos pitagóricos distintos

(Horadam 1961), onde

(Beiler 1966, p. 116). Note que iff é prime ou duas vezes um prime. Os primeiros números para , 2, … são 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1, 1, 4, 1, … (OEIS A046079).

Para encontrar o número de formas em que um número pode ser a hipotenusa de um triângulo primitivo direito, escreva a sua factorização como

onde os s são da forma e os s são da forma . O número de possíveis triângulos direitos primitivos é então

Por exemplo, desde

			(27)
			(28)

Os valores de para , 2, … são 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, … (OIS A024362). Os primeiros primes da forma são 5, 13, 17, 29, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, … (OEIS A002144), portanto os menores comprimentos laterais que são as hipotenas de 1, 2, 4, 8, 16, … triângulos primitivos direitos são 5, 65, 1105, 32045, 1185665, 48612265, … (OEIS A006278).

O número de possíveis triângulos direitos primitivos ou não primitivos tendo como hipotenusa é

			(29)
			(30)

(corrigindo a gralha do Beiler 1966, p. 117, que afirma que esta fórmula dá apenas o número de soluções não-primitivas), onde é a função soma dos quadrados. Por exemplo, existem quatro triângulos inteiros distintos com hipotenusa 65, desde

> Os primeiros números para , 2, … são 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, … (OIS A046080). As menores hipotenus com triplos distintos são 1, 5, 25, 125, 65, 3125, … (OEIS A006339). A tabela seguinte dá as hipotenas para as quais existem exactamente triângulos inteiros distintos para , 1, …, 5.

	OEIS	hypotenuses para os quais existem triângulos inteiros distintos
0	A004144	1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, ….
1	A084645	5, 10, 13, 15, 17, 20, 26, 29, 30, 34, 35, …
2	A084646	25, 50, 75, 100, 150, 169, 175, 200, 225, ….
	A084647	125, 250, 375, 500, 750, 875, 1000, 1125, 1375, …
4	A084648	65, 85, 130, 145, 170, 185, 195, 205, 221, 255, …
5	A084649	3125, 6250, 9375, 12500, 18750, 21875, 25000, …

Por isso, o número total de formas em que pode ser uma perna ou hipotenusa de um triângulo direito é dado por

> Os valores para , 2, … são 0, 0, 1, 1, 2, 1, 1, 2, 2, 2, 2, 1, 4, 2, 1, 5, 3, … (OIS A046081). Os números mais pequenos que podem ser os lados de triângulos direitos gerais para , 2, … são 3, 5, 16, 12, 15, 125, 24, 40, … (OEIS A006593; Beiler 1966, p. 114).

Existem 50 triplos pitagóricos com hipotenusa inferior a 100, os primeiros dos quais, ordenados por aumento , são (3, 4, 5), (6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083, A046084, e A009000).

Destes, apenas 16 são trigémeos primitivos com hipotenusa inferior a 100: (3, 4,5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65), (16, 63, 65), (48, 55, 73), (36, 77, 85), (13, 84, 85), (39, 80, 89), e (65, 72, 97) (OEIS A046086, A046087, e A020882).

Deixe o número de triplos com hipotenusa ser indicado , o número de triplos com hipotenusa ser indicado , e o número de triplos primitivos inferior a ser indicado . Então a tabela seguinte resume os valores para potências de 10,

	OEIS	, , …
	A101929	1, 50, 878, 12467, …
	A101930	2, 52, 881, 12471, …..
	A101931	1, 16, 158, 1593, …

Lehmer (1900) provou que o número de soluções primitivas com hipotenusa é inferior a satisfaz

(OEIS A086201).

Os inradii dos primeiros triângulos pitagóricos primitivos ordenados por aumento são dados por 1, 2, 3, 3, 6, 5, 4, 10, 5, … (OEIS A014498).

Existe um método geral para obter trigêmeos de triângulos pitagóricos com áreas iguais. Pegue os três conjuntos de geradores como

			(34)
			(35)
			(36)
			(37)
			(38)
			(39)

Então o triângulo direito gerado por cada triângulo () tem área comum

(Beiler 1966, pp. 126-127). O único extremo desta função ocorre em . Desde para , a menor área compartilhada por três triângulos direitos não-primitivos é dada por , que resulta em uma área de 840 e corresponde aos trigêmeos (24, 70, 74), (40, 42, 58), e (15, 112, 113) (Beiler 1966, p. 126).

Triângulos rectos cujas áreas consistem num único dígito incluem (área de 6) e (área de 666666; Wells 1986, p. 89).

Em 1643, Fermat desafiou Mersenne a encontrar um trigêmeo pitagórico cuja hipotenusa e soma das pernas fossem quadradas. Fermat encontrou a menor solução desse tipo:

			(41)
			(42)
			(43)

with

			(44)
			(45)

Um problema relacionado é determinar se um número inteiro especificado pode ser a área de um triângulo direito com lados racionais. 1, 2, 3, e 4 não são as áreas de qualquer triângulo direito com lados racionais, mas 5 é (3/2, 20/3, 41/6), assim como 6 é (3, 4, 5). A solução do problema envolve a curva elíptica

Uma solução (, , ) existe se (46) tiver uma solução racional, nesse caso

			(47)
>			(48)

(Koblitz 1993). Não existe um método geral conhecido para determinar se existe uma solução arbitrária , mas uma técnica concebida por J. Tunnell em 1983 permite descartar certos valores (Cipra 1996).