>
>
>
>
>
>
>
>
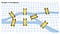
Uma área crescente de interesse para os cientistas que exploram a importância, o poder ou a influência entre as entidades é chamada de Teoria Gráfica. As raízes da Teoria Gráfica começaram em 1736 quando o matemático Carl Ehler apresentou Leonhard Euler ao problema das Pontes de Konigsberg.
O problema das Pontes de Konigsberg está baseado na antiga cidade alemã de Konigsberg, que se situa em ambos os lados do rio Pregel. No centro, havia duas grandes ilhas que estavam ligadas uma à outra e às margens do rio por sete pontes. Carl Ehler ficou obcecado em encontrar uma rota para percorrer cada uma das sete pontes sem passar por nenhuma delas mais do que uma vez. Ehler chegou a Leonhard Euler, um matemático suíço. Euler confirmou a hipótese de Ehler de que o problema não tinha solução, e a explicação de Euler informou um novo paradigma matemático chamado Geometria da Posição.
O novo paradigma geométrico de Euler afirmava que a localização das pontes não importava. O problema, ao invés disso, pode ser simplificado transformando cada ponte em um ponto (nó) com linhas (bordas) para representar as ligações entre elas. Esta prática de usar nós e bordas é agora conhecida como Teoria Gráfica.
Pode ler mais sobre o problema das Pontes em Konigsberg aqui.
Inicialmente, a Teoria Gráfica não serviu muito para a resolução de problemas e não foi muito considerada pelos matemáticos. Contudo, o moderno poder computacional para processar grandes permutações tornou os princípios da Teoria dos Gráficos mais práticos. Este artigo ensina a aplicar os princípios da Teoria Gráfica à análise baseada em Python.

 >
>
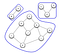
Nem todas as redes de um sistema gráfico estão interligadas. Esta desconexão é quando os componentes são formados. Como mostrado no gráfico abaixo, um componente só é formado quando cada nó tem um caminho para outros nós.
Teoria Aplicada de Gráficos em Python
Em Python, networkx é frequentemente usado para a teoria aplicada de gráficos também conhecida como análise de rede . O pacote tem funcionalidade útil para resumir rapidamente as características de um gráfico. Você pode revisar os passos abaixo e seguir os mesmos passos enquanto criamos um gráfico e entendemos sua composição.
Primeiro o código abaixo cria um objeto vazio no gráfico P. Os próximos passos adicionam nós e descrevem as bordas.
Argumentos como <object>.nodes() ou <object>.edges() são formas rápidas de visualizar todos os nós e bordas do sistema gráfico.
print(P.nodes())print(P.edges())
Finalmente, nx.draw é usado para visualizar a rede.
%matplotlib inline
import matplotlib.pyplot as plt
nx.draw(P, with_labels = True)
>
Exercícios 1:
Agora que os conceitos básicos dos gráficos são discutidos, os seguintes exercícios são um bom método para praticar:
- Quantos nós estão no gráfico acima?
- Quantos nós estão no gráfico acima?
- Qual é o Geodésico para E e C?
- Existe mais de 1 componente no gráfico?
Usando Dados Reais
O exercício abaixo usará dados para vôos dentro dos Estados Unidos em 2015. O conjunto de dados inclui os aeroportos de origem e destino, além de atributos que descrevem o tempo e os atrasos do voo (meteorologia, segurança ou relacionados com a companhia aérea).
Porque o conjunto de dados é grande, o exercício irá concentrar-se em voos originários dos aeroportos da área de Los Angeles (Los Angeles (LAX), Burbank (BUR), Orange County (SNA), e San Bernardino County (ONT)). Além disso, o foco será rever vôos que se assemelham ao meu horário de viagem Deloitte – voando aos domingos e retornando às quintas-feiras.
Desde que já temos dados de origem e destino, ****fields ORIGIN_AIRPORT e DESTINATION_AIRPORT servirão como campos de origem para nós e bordas – não há necessidade de criar nós ou bordas como fizemos no primeiro exercício. Uma vez definidos os nós, <object>.edges() irá fornecer todas as relações de par entre eles. Finalmente, nx.draw irá ajudar a produzir um gráfico para as arestas.

FG.edges()

nx.draw(FG, with_labels = True)

>
Na saída acima, Os nós são etiquetados com Códigos de Aeroportos. Todas as bordas levam a um dos quatro aeroportos da área de Los Angeles porque esses quatro foram os únicos selecionados para esse exercício. Los Angeles International (LAX) é o maior aeroporto entre os quatro e o gráfico mostra claramente que muitas cidades são acessíveis apenas para LAX e não a partir de outros aeroportos menores. Isto mostra a conectividade, ou centralidade de graus, de LAX. Em networkx, nx.algorithms.degree_centrality(<object>) **** é usado para encontrar a centralidade de cada nó no sistema gráfico.
# Calculating the centrality of each of the airports
nx.algorithms.degree_centrality(FG)
Podemos ir mais granular e usar um curto ‘for loop’ para produzir bordas entre duas áreas de interesse. Por exemplo, o seguinte código é usado para encontrar todos os voos possíveis do condado de San Bernardino (ONT) para Newark (EWR) no domingo ou quinta-feira.
Dentre as várias opções de voo entre o condado de San Bernardino e Newark, o nx.dijkstra_path pode ser usado para encontrar o caminho Euclidiano (ou o caminho mais curto).
#Finding the dijkstra path
djk_path = nx.dijkstra_path(FG, source='ONT', target='EWR')
djk_path
Exercícios 2:
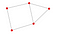
- Produzir o seguinte gráfico usando
nx.draw(). Nota: sua rede pode não parecer exatamente a mesma, mas os caminhos, bordas e nós devem corresponder à rede abaixo. - Imprimir todas as bordas.
- Qual é o caminho mais curto de L a F?

>