Durante os séculos XVII e especialmente XVIII, Impulsionados tanto pelo desejo de compreender a natureza como pela busca de fazer balões nos quais pudessem voar (Figura 1), vários cientistas estabeleceram as relações entre as propriedades físicas macroscópicas dos gases, ou seja, pressão, volume, temperatura e quantidade de gás. Embora suas medidas não fossem precisas pelos padrões atuais, eles foram capazes de determinar as relações matemáticas entre pares dessas variáveis (por exemplo, pressão e temperatura, pressão e volume) que sustentam para um gás ideal – uma construção hipotética que os gases reais se aproximam sob certas condições. Eventualmente, essas leis individuais foram combinadas em uma única equação – a lei do gás ideal – que relaciona quantidades de gás para gases e é bastante precisa para baixas pressões e temperaturas moderadas. Consideraremos os principais desenvolvimentos nas relações individuais (por razões pedagógicas não muito bem ordenadas historicamente) e depois os colocaremos juntos na lei do gás ideal.

Figure 1. Em 1783, ocorreu o primeiro (a) vôo de balão cheio de hidrogênio, (b) vôo de balão de ar quente tripulado, e (c) vôo de balão cheio de hidrogênio tripulado. Quando o balão cheio de hidrogênio descrito em (a) pousou, os moradores assustados de Gonesse supostamente o destruíram com forquilhas e facas. O lançamento deste último foi alegadamente visto por 400.000 pessoas em Paris.

Pressão e Temperatura: Lei de Gay-Lussac

Imagine encher um recipiente rígido ligado a um manómetro com gás e depois selar o recipiente para que nenhum gás possa escapar. Se o recipiente é resfriado, o gás no interior também fica mais frio e sua pressão é observada a diminuir. Como o recipiente é rígido e bem vedado, tanto o volume quanto o número de moles de gás permanecem constantes. Se aquecermos a esfera, o gás no interior fica mais quente (Figura 2) e a pressão aumenta.

Figure 2. O efeito da temperatura sobre a pressão do gás: Quando a placa quente está desligada, a pressão do gás na esfera é relativamente baixa. medida que o gás é aquecido, a pressão do gás na esfera aumenta.

Esta relação entre temperatura e pressão é observada para qualquer amostra de gás confinada a um volume constante. Um exemplo de dados experimentais de pressão-temperatura é mostrado para uma amostra de ar sob estas condições na Figura 3. Verificamos que a temperatura e a pressão estão linearmente relacionadas, e se a temperatura está na escala de kelvin, então P e T são diretamente proporcionais (novamente, quando o volume e moles de gás são mantidos constantes); se a temperatura na escala de kelvin aumenta por um determinado fator, a pressão do gás aumenta pelo mesmo fator.

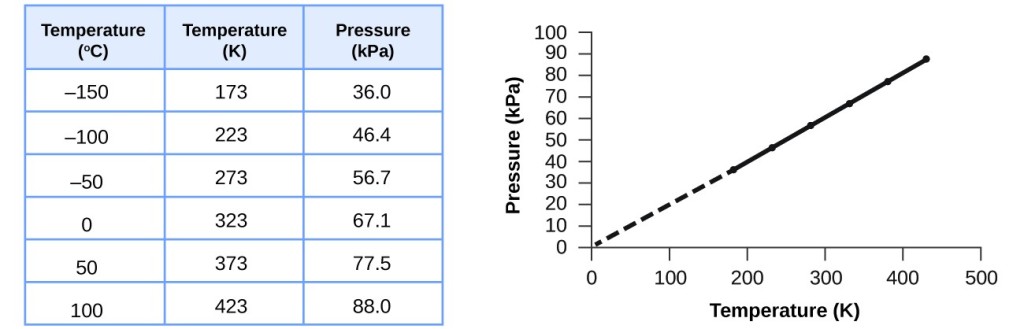
Figure 3. Para um volume e quantidade de ar constantes, a pressão e temperatura são diretamente proporcionais, desde que a temperatura esteja em kelvin. (As medições não podem ser feitas a temperaturas mais baixas por causa da condensação do gás). Quando esta linha é extrapolada para pressões mais baixas, atinge uma pressão de 0 a -273 °C, que é 0 na escala de kelvin e a temperatura mais baixa possível, chamada de zero absoluto.

Guillaume Amontons foi o primeiro a estabelecer empiricamente a relação entre a pressão e a temperatura de um gás (~1700), e Joseph Louis Gay-Lussac determinou a relação com maior precisão (~1800). Por causa disso, a relação P-T para gases é conhecida como a lei de Gay-Lussac ou Lei de Amontons. Sob qualquer dos nomes, ela afirma que a pressão de uma determinada quantidade de gás é diretamente proporcional à sua temperatura na escala de kelvin quando o volume é mantido constante. Matematicamente, isto pode ser escrito:

\larga P\propto T

\larga P=\texto{constante}\times T

\larga P=k\times T

where ∝ significa “é proporcional a”, e k é uma constante de proporcionalidade que depende da identidade, quantidade e volume do gás.

\larga\frac{{P}_{1}}{{T}_{1}}=\frac{{P}_{2}}{{T}_{2}}

Esta equação é útil para cálculos de pressão-temperatura para um gás confinado em volume constante. Note que as temperaturas devem estar na escala de kelvin para qualquer cálculo da lei do gás (0 na escala de kelvin e a temperatura mais baixa possível é chamada de zero absoluto). (Observe também que há pelo menos três maneiras de descrever como a pressão de um gás muda à medida que a sua temperatura muda: Podemos usar uma tabela de valores, um gráfico, ou uma equação matemática.)

Volume e Temperatura: Lei de Charles

Se enchermos um balão com ar e o selarmos, o balão contém uma quantidade específica de ar à pressão atmosférica, digamos 1 atm. Se colocarmos o balão em uma geladeira, o gás dentro da geladeira fica frio e o balão encolhe (embora tanto a quantidade de gás quanto a sua pressão permaneçam constantes). Se fizermos o balão muito frio, ele encolherá muito, e se expande novamente quando aquece.

Estes exemplos do efeito da temperatura sobre o volume de uma dada quantidade de um gás confinado a uma pressão constante são verdadeiros em geral: O volume aumenta à medida que a temperatura aumenta, e diminui à medida que a temperatura diminui. Os dados de volume e temperatura para uma amostra de 1 ml de gás metano a 1 atm são listados e grafados na Figura 4.

Figure 4. O volume e a temperatura estão linearmente relacionados para 1 mol de gás metano a uma pressão constante de 1 atm. Se a temperatura estiver em kelvin, o volume e a temperatura são directamente proporcionais. A linha pára em 111 K porque o metano se liquefaz a esta temperatura; quando extrapolada, intercepta a origem do gráfico, representando uma temperatura de zero absoluto.

A relação entre o volume e a temperatura de uma dada quantidade de gás a pressão constante é conhecida como a lei de Charles em reconhecimento do cientista francês e pioneiro do vôo de balão Jacques Alexandre César Charles. A lei de Charles afirma que o volume de uma dada quantidade de gás é diretamente proporcional à sua temperatura na escala de kelvin quando a pressão é mantida constante.

Matematicamente, isto pode ser escrito como:

\larga V\propto T

\larga V=\text{constante}\cdot T

\larga V=k\cdot T

sendo k uma constante de proporcionalidade que depende da quantidade e pressão do gás.

>

\larga\frac{{V}_{1}}{{T}_{1}}=\frac{{{V}_{2}}{{T}_{2}}

Volume e Pressão: Lei de Boyle

Se enchermos parcialmente uma seringa hermética com ar, a seringa contém uma quantidade específica de ar a temperatura constante, digamos 25 °C. Se empurrarmos lentamente o êmbolo mantendo a temperatura constante, o gás da seringa é comprimido num volume menor e a sua pressão aumenta; se puxarmos o êmbolo para fora, o volume aumenta e a pressão diminui. Este exemplo do efeito do volume sobre a pressão de uma dada quantidade de um gás confinado é verdadeiro em geral. Diminuir o volume de um gás confinado aumentará a sua pressão, e aumentar o seu volume diminuirá a sua pressão. Na verdade, se o volume aumenta por um determinado fator, a pressão diminui pelo mesmo fator, e vice-versa. Os dados de pressão volumétrica para uma amostra de ar à temperatura ambiente são mostrados na Figura 5.

Figure 5. Quando um gás ocupa um volume menor, ele exerce uma pressão maior; quando ocupa um volume maior, ele exerce uma pressão menor (assumindo que a quantidade de gás e a temperatura não mudam). Uma vez que P e V são inversamente proporcionais, um gráfico de 1/P vs. V é linear.

Descomo as relações P-T e V-T, pressão e volume não são diretamente proporcionais um ao outro. Ao invés disso, P e V exibem proporcionalidade inversa: Aumentar a pressão resulta numa diminuição do volume do gás. Matematicamente, isto pode ser escrito:

\larga P\propto 1\text{/}V\text{/}V=k\cdot 1\text{/}V\text{/}V\text{ ou }P\cdot V=k\text{ ou }{P}_{1}{V}_{1}={P}_{2}{V}_{2}

sendo k uma constante. Graficamente, esta relação é mostrada pela linha reta que resulta quando se plota o inverso da pressão (V). Gráficos com linhas curvas são difíceis de ler com precisão em valores baixos ou altos das variáveis, e são mais difíceis de usar no ajuste de equações teóricas e parâmetros aos dados experimentais. Por essas razões, os cientistas frequentemente tentam encontrar uma forma de “linearizar” os seus dados. Se traçarmos P versus V, obtemos uma hiperbola (ver Figura 6).

A relação entre o volume e a pressão de uma dada quantidade de gás a temperatura constante foi publicada pela primeira vez pelo filósofo natural inglês Robert Boyle há mais de 300 anos. Ela está resumida na declaração agora conhecida como a lei de Boyle: O volume de uma dada quantidade de gás mantido a temperatura constante é inversamente proporcional à pressão sob a qual é medido.

Chemistry in Action: Respiração e Lei de Boyle

O que você faz cerca de 20 vezes por minuto durante toda a sua vida, sem pausas e, muitas vezes, sem sequer estar consciente disso? A resposta, é claro, é respiração, ou respiração. Como é que funciona? Acontece que as leis dos gases se aplicam aqui. Seus pulmões absorvem os gases que seu corpo precisa (oxigênio) e se livram dos gases residuais (dióxido de carbono). Os pulmões são feitos de tecido esponjoso e elástico que se expande e contrai enquanto você respira. Quando inspira, o seu diafragma e os músculos intercostais (os músculos entre as costelas) contraem-se, expandindo a sua cavidade torácica e tornando o seu volume pulmonar maior. O aumento do volume leva a uma diminuição da pressão (lei de Boyle). Isto faz com que o ar flua para os pulmões (de alta pressão para baixa pressão). Quando você expira, o processo se inverte: Os músculos do diafragma e das costelas relaxam, a cavidade torácica contrai-se e o volume pulmonar diminui, fazendo com que a pressão aumente (a lei de Boyle novamente), e o ar sai dos pulmões (de alta pressão para baixa pressão). Você então inspira e expira novamente, e novamente, repetindo este ciclo da lei de Boyle para o resto de sua vida (Figura 7).

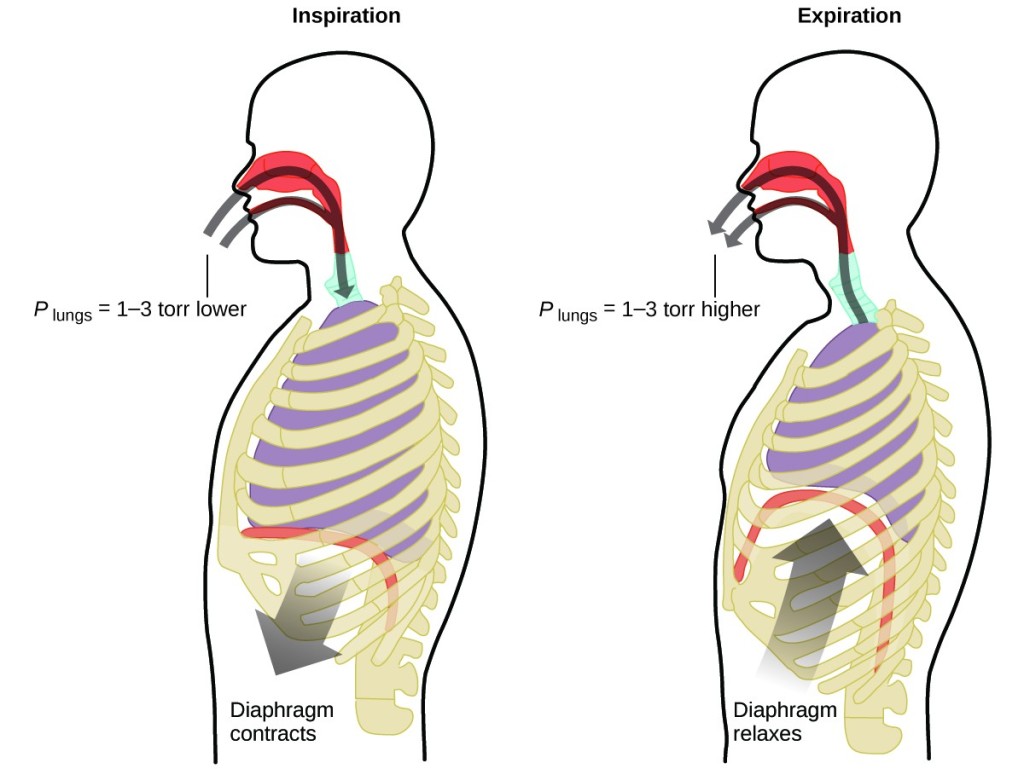
Figure 7. A respiração ocorre porque a expansão e contração do volume pulmonar cria pequenas diferenças de pressão entre seus pulmões e seu ambiente, fazendo com que o ar seja sugado para dentro e forçado para fora de seus pulmões.

Moles de Gás e Volume: Lei de Avogadro

O cientista italiano Amedeo Avogadro avançou uma hipótese em 1811 para contabilizar o comportamento dos gases, afirmando que volumes iguais de todos os gases, medidos sob as mesmas condições de temperatura e pressão, contêm o mesmo número de moléculas. Ao longo do tempo, esta relação foi apoiada por muitas observações experimentais, como expresso pela lei de Avogadro: Para um gás confinado, o volume (V) e o número de moles (n) são diretamente proporcionais se a pressão e a temperatura permanecerem constantes.

Em forma de equação, isto é escrito como:

>

\larga\begin{array}{ccccc}V\propto n& {ou}& V=k\times n& \texto{ou}& \{V}_{1}{n}_{1}}=frac{V}_{2}}{{n}_{2}}}{n}_{2}}end{array}

As relações matemáticas também podem ser determinadas para os outros pares de variáveis, tais como P contra n, e n contra T.

Glossary

Nulo absoluto: temperatura na qual o volume de um gás seria zero de acordo com a lei de Charles.

A lei de Avogadro: volume de um gás a temperatura e pressão constantes é proporcional ao número de moléculas de gás

A lei de Boyle: volume de um dado número de moléculas de gás mantidas a temperatura constante é inversamente proporcional à pressão sob a qual é medida

A lei de Charles: o volume de um dado número de moles de gás é directamente proporcional à sua temperatura kelvin quando a pressão é mantida constante

Lei de Gay-Lussac: (também, lei de Amontons) a pressão de um dado número de moles de gás é diretamente proporcional à sua temperatura kelvin quando a pressão é mantida constante