Superior a 90% dos sólidos naturais e sintéticos são cristalinos. A maioria dos sólidos se forma com uma disposição regular de suas partículas, porque as interações atrativas gerais entre as partículas são maximizadas, e a energia total intermolecular é minimizada, quando as partículas se empacotam da maneira mais eficiente. O arranjo regular a nível atômico é freqüentemente refletido a nível macroscópico. Neste módulo, vamos explorar alguns dos detalhes sobre as estruturas dos sólidos cristalinos metálicos e iônicos, e aprender como estas estruturas são determinadas experimentalmente.

As Estruturas dos Metais

Vamos começar a nossa discussão sobre sólidos cristalinos considerando os metais elementares, que são relativamente simples porque cada um contém apenas um tipo de átomo. Um metal puro é um sólido cristalino com átomos metálicos compactados em um padrão repetitivo. Algumas das propriedades dos metais em geral, tais como a sua maleabilidade e ductilidade, devem-se em grande parte a ter átomos idênticos dispostos num padrão regular. As diferentes propriedades de um metal em relação a outro dependem parcialmente do tamanho dos seus átomos e das especificidades da sua disposição espacial. Vamos explorar as semelhanças e diferenças de quatro das geometrias mais comuns dos cristais metálicos nas secções que se seguem.

Células unitárias de Metais

A estrutura de um sólido cristalino, quer seja um metal ou não, é melhor descrita considerando a sua unidade de repetição mais simples, que é referida como a sua célula unitária. A célula unitária consiste em pontos de malha que representam as localizações dos átomos ou íons. Toda a estrutura consiste então nesta célula unitária que se repete em três dimensões, como ilustrado na Figura 1.

Figure 1. Uma célula unitária mostra as localizações dos pontos da malha repetindo em todas as direções.

Deixe-nos começar nossa investigação da estrutura da malha de cristal e células unitárias com a estrutura mais direta e a célula unitária mais básica. Para visualizar isso, imagine pegar um grande número de esferas idênticas, como bolas de tênis, e arrumá-las uniformemente em um recipiente. A maneira mais simples de fazer isso seria fazer camadas nas quais as esferas de uma camada estão diretamente acima das da camada abaixo, como ilustrado na Figura 2. Este arranjo é chamado de estrutura cúbica simples, e a célula unitária é chamada de célula unitária simples ou célula cúbica primitiva.

Figure 2. Quando átomos metálicos são dispostos com esferas em uma camada diretamente acima ou abaixo de esferas em outra camada, a estrutura da malha é chamada de cúbica simples. Note que as esferas estão em contato.

Em uma estrutura cúbica simples, as esferas não são empacotadas o mais próximo possível, e elas “enchem” apenas cerca de 52% do volume do recipiente. Este é um arranjo relativamente ineficiente, e apenas um metal (polónio, Po) se cristaliza numa estrutura cúbica simples. Como mostrado na Figura 3, um sólido com este tipo de arranjo consiste em planos (ou camadas) nos quais cada átomo entra em contato apenas com os quatro vizinhos mais próximos em sua camada; um átomo diretamente acima dele na camada acima; e um átomo diretamente abaixo dele na camada abaixo. O número de outras partículas que cada partícula em um contato sólido cristalino é conhecido como seu número de coordenação. Para um átomo de polônio em uma matriz cúbica simples, o número de coordenação é, portanto, seis.

Figure 3. Um átomo em uma estrutura de árvore cúbica simples entra em contato com seis outros átomos, portanto tem um número de coordenação de seis.

Em uma árvore cúbica simples, a célula unitária que se repete em todas as direções é um cubo definido pelos centros de oito átomos, como mostrado na Figura 4. Os átomos nos cantos adjacentes desta célula unitária entram em contato entre si, de modo que o comprimento da borda desta célula é igual a dois raios atômicos, ou seja, um diâmetro atômico. Uma célula de unidade cúbica contém apenas as partes destes átomos que estão dentro dela. Como um átomo em um canto de uma célula de unidade cúbica simples é contido por um total de oito células unitárias, apenas um oitavo desse átomo está dentro de uma célula unitária específica. E como cada célula de unidade cúbica simples tem um átomo em cada um de seus oito “cantos”, há 8 \frac{1}{8}=1 átomo dentro de uma célula de unidade cúbica simples.

Figure 4. Uma célula de unidade cúbica simples contém um oitavo de um átomo em cada um dos seus oito cantos, portanto contém um átomo total.

Exemplo 1: Cálculo do Raio Atômico e Densidade para Metais, Parte 1

O comprimento da borda da célula da unidade de polônio alfa é 336 pm.

1. Determinar o raio de um átomo de polónio.
2. Determinar a densidade de polónio alfa.

Mostrar solução

Cristaliza o polónio alfa numa célula de unidade cúbica simples:

1. Dois átomos Po adjacentes entram em contacto entre si, pelo que o comprimento da borda desta célula é igual a dois raios atómicos de Po: l=2r. A densidade do polónio pode ser encontrada determinando a densidade da sua célula unitária (a massa contida numa célula unitária dividida pelo volume da célula unitária). Uma vez que uma célula de unidade Po contém um oitavo de um átomo de Po em cada um de seus oito cantos, uma célula de unidade contém um átomo de Po.

A massa de uma célula de unidade Po pode ser encontrada por:

\texto{1 célula de unidade Po}}{1 célula de unidade Po}{1 átomo de Po}{1 célula de unidade Po}{1 célula de unidade Po}}{6.022 vezes 10 23 texto Atomos Po vezes 208.998 texto G Texto 1 mol Po = 3.47 vezes {10}^{-22}text{g}

O volume de uma célula da unidade Po pode ser encontrado por:

V={l}^{3}={(336}times {10}^{-10}{cm}} }^{3}=3.79\ vezes {10}^{-23}{\texto{cm}}^{3}

(Note que o comprimento da borda foi convertido de pm para cm para obter as unidades de volume habituais para densidade.)

Por isso, a densidade de \texto{Po}=dfrac{3.471\ vezes {10}^{-22}}text{g}}{3.79\ vezes {10}^{-23}{\texto{cm}}^{3}={\texto{9.16 g/cm}}^{3}

Check Your Learning

O comprimento da borda da célula da unidade para o níquel é 0.3524 nm. A densidade de Ni é de 8,90 g/cm3. O níquel cristaliza em uma estrutura cúbica simples? Explique.

Mostrar solução

Não. Se Ni fosse cúbico simples, a sua densidade seria dada por:

\texto{1 átomo de Ni}{1 mol Ni}}{6.022\ vezes {10}^{23}text{Ni atoms}}}times {58.693}text{g}{1 mol Ni}}=9.746\times {10}^{-23}text{g}
V={l}^{3}={(3.524\\posições {10}^{-8}\posições {cm})^{3}=4.376\posições {10}^{-23}{\posições {cm}}^{3}

Então a densidade de Ni seria =\\posições {9.746\posições {10}^{-23}{g}{4.376\posições {10}^{-23}{\posições {cm}^{3}={\posições {2.23 g/cm}}^{3}

Desde que a densidade real de Ni não esteja próxima disso, Ni não forma uma simples estrutura cúbica.

A maioria dos cristais metálicos é um dos quatro principais tipos de células unitárias. Por enquanto, vamos focar nas três células de unidade cúbica: célula cúbica simples (que já vimos), célula cúbica centrada no corpo e célula cúbica centrada na face – todas ilustradas na Figura 5. (Note que existem de fato sete sistemas diferentes de estrutura, alguns dos quais têm mais de um tipo de estrutura, para um total de 14 tipos diferentes de células unitárias. Deixamos as geometrias mais complicadas para mais tarde neste módulo.)

Figure 5. As células de unidade cúbica de metais mostram (nas figuras superiores) a localização dos pontos de malha e (nas figuras inferiores) os átomos de metal localizados na célula unitária.

alguns metais cristalizam num arranjo que tem uma célula unitária cúbica com átomos em todos os cantos e um átomo no centro, como mostra a Figura 6. Isto é chamado de sólido cúbico centrado no corpo (BCC). Os átomos nos cantos de uma célula de unidade BCC não entram em contato um com o outro, mas entram em contato com o átomo no centro. Uma célula de unidade BCC contém dois átomos: um oitavo de um átomo em cada um dos oito cantos ( 8 vezes \frac{1}{8}=1 átomo dos cantos) mais um átomo do centro. Qualquer átomo nesta estrutura toca quatro átomos na camada acima dele e quatro átomos na camada abaixo dele. Assim, um átomo em uma estrutura BCC tem um número de coordenação de oito.

Figure 6. Numa estrutura cúbica centrada no corpo, os átomos numa camada específica não se tocam uns aos outros. Cada átomo toca quatro átomos na camada acima dele e quatro átomos na camada abaixo dele.

Os átomos em arranjos BCC são embalados de forma muito mais eficiente do que numa estrutura cúbica simples, ocupando cerca de 68% do volume total. Os metais isomórficos com estrutura BCC incluem K, Ba, Cr, Mo, W, e Fe à temperatura ambiente. (Elementos ou compostos que cristalizam com a mesma estrutura são ditos isomórficos)

Muitos outros metais, como alumínio, cobre e chumbo, cristalizam em um arranjo que tem uma célula cúbica com átomos em todos os cantos e nos centros de cada face, como ilustrado na Figura 7. Este arranjo é chamado de sólido cúbico centrado na face (FCC). Uma célula da unidade FCC contém quatro átomos: um oitavo de um átomo em cada um dos oito cantos ( 8 vezes \frac{1}{8}=1 átomo dos cantos) e metade de um átomo em cada uma das seis faces (6\frac{1}{2}=3 átomos das faces). Os átomos nos cantos tocam os átomos nos centros das faces adjacentes ao longo das diagonais da face do cubo. Como os átomos estão em pontos de malha idênticos, eles têm ambientes idênticos.

Figure 7. Um sólido cúbico centrado na face tem átomos nos cantos e, como o nome indica, nos centros das faces das suas células unitárias.

Os átomos num arranjo FCC são embalados o mais próximo possível, com átomos que ocupam 74% do volume. Esta estrutura também é chamada de embalagem cúbica mais próxima (CCP). No CCP, existem três camadas repetidas de átomos dispostos hexagonalmente. Cada átomo contata seis átomos em sua própria camada, três na camada acima e três na camada abaixo. Nesse arranjo, cada átomo toca 12 perto dos vizinhos, e portanto tem um número de coordenação de 12. O fato de que os arranjos FCC e CCP são equivalentes pode não ser imediatamente óbvio, mas porque eles são na verdade a mesma estrutura é ilustrado na Figura 8.

Figure 8. Um arranjo CCP consiste em três camadas repetidas (ABCABC…) de átomos dispostos de forma hexagonal. Os átomos de uma estrutura CCP têm um número de coordenação de 12 porque contactam seis átomos na sua camada, mais três átomos na camada acima e três átomos na camada abaixo. Girando nossa perspectiva, podemos ver que uma estrutura PCC tem uma célula unitária com uma face contendo um átomo da camada A em um canto, átomos da camada B através de uma diagonal (em dois cantos e no meio da face), e um átomo da camada C no canto restante. Isto é o mesmo que um arranjo cúbico centrado na face.

Porque uma embalagem mais próxima maximiza as atrações gerais entre os átomos e minimiza a energia intermolecular total, os átomos na maioria dos metais embalam desta forma. Encontramos dois tipos de empacotamento mais próximos em estruturas metálicas cristalinas simples: CCP, que já encontramos, e o empacotamento hexagonal mais próximo (HCP) mostrado na Figura 9. Ambos consistem em camadas repetidas de átomos dispostos de forma hexagonal. Em ambos os tipos, uma segunda camada (B) é colocada na primeira camada (A) para que cada átomo da segunda camada esteja em contacto com três átomos da primeira camada. A terceira camada é posicionada de uma de duas maneiras. No HCP, os átomos da terceira camada estão directamente acima dos átomos da primeira camada (ou seja, a terceira camada também é do tipo A), e o empilhamento consiste em camadas alternadas de tipo A e de tipo B fechadas (ou seja, ABABAB⋯). No CCP, os átomos da terceira camada não estão acima dos átomos de nenhuma das duas primeiras camadas (ou seja, a terceira camada é do tipo C), e o empilhamento consiste em camadas alternadas de tipo A, tipo B e tipo C fechadas (ou seja, ABCABCABC⋯). Cerca de dois terços de todos os metais se cristalizam em matrizes mais próximas, com números de coordenação de 12. Metais que cristalizam em uma estrutura HCP incluem Cd, Co, Li, Mg, Na, e Zn, e metais que cristalizam em uma estrutura CCP incluem Ag, Al, Ca, Cu, Ni, Pb, e Pt.

Figure 9. Em ambos os tipos de embalagem mais próxima, os átomos são embalados da forma mais compacta possível. A embalagem hexagonal mais próxima consiste em duas camadas alternadas (ABABAB…). O empacotamento cúbico mais próximo consiste de três camadas alternadas (ABCABCABC…).

Exemplo 2: Cálculo do Raio Atômico e Densidade para Metais, Parte 2

Cálcio cristaliza em uma estrutura cúbica centrada na face. O comprimento da sua célula unitária é 558.8 pm.

1. Qual é o raio atómico de Ca nesta estrutura?
2. Calcular a densidade de Ca.

Mostrar Solução

Parte 1

Em uma estrutura FCC, os átomos Ca entram em contato entre si através da diagonal da face, de modo que o comprimento da diagonal é igual a quatro raios atômicos Ca (d = 4r). 8\text{pm})}^{2}+{(558.5\text{pm})}^{2}={(4r)}^{2}

Solving this gives r=\sqrt{\dfrac{{(558.8\text{pm})}^{2}+{(558. A densidade do cálcio pode ser encontrada pela determinação da densidade da sua célula unitária: por exemplo, a massa contida numa célula unitária dividida pelo volume da célula unitária. Uma célula de unidade Ca centrada na face tem um oitavo de um átomo em cada um dos oito cantos à esquerda (8 vezes à direita) e metade de um átomo em cada uma das seis faces à esquerda (6 vezes à direita), para um total de quatro átomos na célula de unidade.

A massa da célula da unidade pode ser encontrada por:

>text{1 Célula da unidade Ca}{1 vezes {4 átomos Ca}}{1 célula da unidade Ca}{1 mol Ca}{6.022 vezes {10}{23}textos {Ca átomos} {40.078}textos {g}{1 mol Ca}=2.662\ vezes {10}^{-22}textos{g}

O volume de uma célula Ca pode ser encontrado por:

V={a}^{3}={(558.8}{10}^{-10}{cm})}^{3}=1.745\\ vezes {10}^{-22}{\texto{cm}}^{3}

(Note que o comprimento da borda foi convertido de pm para cm para obter as unidades de volume habituais para densidade.)

Então, a densidade de \texto{Ca}=\frac{2,662}vezes {10}^{-22}{g}{1,745}vezes {10}^{-22}{cm}}^{3}={1.53 g/cm}}^{3}

Check Your Learning

Silver crystallizes in an FCC structure. O comprimento da borda de sua célula unitária é 409 pm.

1. Qual é o raio atômico do Ag nesta estrutura?
2. Calcular a densidade do Ag.

Mostrar Soluções

1. 144 pm
2. 10.5 g/cm3

Em geral, uma célula unitária é definida pelo comprimento de três eixos (a, b, e c) e pelos ângulos (α, β, e γ) entre eles, como ilustrado na Figura 10. Os eixos são definidos como sendo os comprimentos entre os pontos da malha espacial. Conseqüentemente, os eixos das células unitárias unem pontos com ambientes idênticos.

Figure 10. Uma célula unitária é definida pelo comprimento de seus três eixos (a, b, e c) e pelos ângulos (α, β, e γ) entre os eixos.

Existem sete sistemas diferentes de malha, alguns dos quais com mais de um tipo de malha, para um total de catorze células unitárias diferentes, que têm as formas mostradas na Figura 11.

Figure 11. Existem sete sistemas de grelha diferentes e 14 células unitárias diferentes.

As Estruturas de Cristais Iónicos

Cristais Iónicos consistem em dois ou mais tipos diferentes de iões que normalmente têm tamanhos diferentes. A embalagem destes iões numa estrutura de cristal é mais complexa que a embalagem de átomos de metal do mesmo tamanho.

Os iões mais monatómicos comportam-se como esferas carregadas, e a sua atracção por iões de carga oposta é a mesma em todas as direcções. Consequentemente, estruturas estáveis para compostos iônicos resultam (1) quando íons de uma carga estão rodeados pelo maior número possível de íons da carga oposta e (2) quando os cátions e ânions estão em contato um com o outro. As estruturas são determinadas por dois fatores principais: os tamanhos relativos dos íons e a razão entre o número de íons positivos e negativos no composto.

Figure 12. Os cátions podem ocupar dois tipos de furos entre os ânions: furos octaédricos ou tetraédricos.

Em estruturas iônicas simples, normalmente encontramos os ânions, que são normalmente maiores que os cátions, dispostos em um conjunto mais próximo. (Como visto anteriormente, elétrons adicionais atraídos para o mesmo núcleo tornam os ânions maiores e menos elétrons atraídos para o mesmo núcleo tornam os cátions menores quando comparados com os átomos a partir dos quais eles são formados). Os catiões menores normalmente ocupam um dos dois tipos de orifícios (ou interstícios) que restam entre os ânions. O menor dos furos é encontrado entre três ânions em um plano e um ânion em um plano adjacente. Os quatro ânions ao redor deste buraco estão dispostos nos cantos de um tetraedro, por isso o buraco é chamado de buraco tetraédrico. O tipo maior de buraco é encontrado no centro de seis ânions (três em uma camada e três em uma camada adjacente) localizados nos cantos de um octaedro; isto é chamado de buraco octaédrico. A Figura 12 ilustra ambos os tipos de furos.

Dependente dos tamanhos relativos dos cátions e ânions, os cátions de um composto iônico podem ocupar furos tetraédricos ou octaédricos, como ilustrado na Figura 13. Cátions relativamente pequenos ocupam furos tetraédricos, e cátions maiores ocupam furos octaédricos. Se os cátions são muito grandes para caberem nos buracos octaédricos, os ânions podem adotar uma estrutura mais aberta, tal como uma simples matriz cúbica. Os cátions maiores podem então ocupar os buracos cúbicos maiores tornados possíveis pelo espaçamento mais aberto.

Figure 13. O tamanho de um catião e a forma do buraco ocupado pelo composto estão diretamente relacionados.

Existem dois buracos tetraédricos para cada ânion em uma matriz de ânions HCP ou CCP. Um composto que se cristaliza em uma matriz de ânions mais próxima com cátions nos furos tetraédricos pode ter uma razão máxima de cátion:ânion de 2:1; todos os furos tetraédricos são preenchidos com esta razão. Exemplos incluem Li2O, Na2O, Li2S, e Na2S. Compostos com uma razão de menos de 2:1 também podem cristalizar em um conjunto mais próximo de ânions com cátions nos furos tetraédricos, se os tamanhos iônicos se ajustarem. Nestes compostos, contudo, alguns dos orifícios tetraédricos permanecem vagos.

A relação entre os buracos octaédricos e os ânions de uma estrutura HCP ou CCP é de 1:1. Assim, compostos com cátions em buracos octaédricos em uma matriz de ânions mais próxima podem ter uma razão máxima de cátion:ânion de 1:1. Em NiO, MnS, NaCl, e KH, por exemplo, todos os buracos octaédricos são preenchidos. Razões inferiores a 1:1 são observadas quando alguns dos buracos octaédricos permanecem vazios.

Em uma simples matriz cúbica de ânions, há um buraco cúbico que pode ser ocupado por um catião para cada ânion na matriz. Em CsCl, e em outros compostos com a mesma estrutura, todos os furos cúbicos são ocupados. Metade dos furos cúbicos são ocupados em SrH2, UO2, SrCl2, e CaF2.

Diferentes tipos de compostos iônicos freqüentemente se cristalizam na mesma estrutura quando os tamanhos relativos de seus íons e suas estequiometrias (as duas principais características que determinam a estrutura) são semelhantes.

Células unitárias de compostos iônicos

Muitos compostos iônicos cristalizam com células unitárias cúbicas, e nós usaremos estes compostos para descrever as características gerais das estruturas iônicas.

Quando um composto iônico é composto de cátions e ânions de tamanho semelhante em uma proporção de 1:1, ele tipicamente forma uma estrutura cúbica simples. Cloreto de césio, CsCl, (ilustrado na Figura 14) é um exemplo disso, com Cs+ e Cl- tendo raios de 174 pm e 181 pm, respectivamente. Podemos pensar nisto como íons cloreto formando uma célula unitária simples, com um íon de césio no centro; ou como íons césio formando uma célula unitária com um íon cloreto no centro; ou como células unitárias simples formadas por íons Cs+ células unitárias sobrepostas formadas por íons Cl-. Os íons Césios e os íons cloreto se tocam ao longo das diagonais do corpo das células unitárias. Um íon de césio e um íon de cloreto estão presentes por unidade de célula, dando a estequiometria l:l requerida pela fórmula do cloreto de césio. Note que não há um ponto de malha no centro da célula, e CsCl não é uma estrutura BCC porque um íon de césio não é idêntico a um íon de cloreto.

Figure 14. Compostos iônicos com cátions e ânions de tamanho semelhante, como o CsCl, geralmente formam uma estrutura cúbica simples. Eles podem ser descritos por células unitárias com cátions nos cantos ou ânions nos cantos.

Dissemos que a localização dos pontos de treliça é arbitrária. Isto é ilustrado por uma descrição alternativa da estrutura CsCl na qual os pontos da malha estão localizados nos centros dos íons de césio. Nesta descrição, os íons césio estão localizados nos pontos da malha nos cantos da célula, e o íon cloreto está localizado no centro da célula. As duas células unitárias são diferentes, mas descrevem estruturas idênticas.

Quando um composto iônico é composto por uma razão de 1:1 de cátions e ânions que diferem significativamente em tamanho, ele normalmente se cristaliza com uma célula unitária de FCC, como a mostrada na Figura 15. Cloreto de sódio, NaCl, é um exemplo disso, com Na+ e Cl- tendo raios de 102 pm e 181 pm, respectivamente. Podemos pensar nisto como íons cloreto formando uma célula FCC, com íons sódio localizados nos orifícios octaédricos no meio das bordas da célula e no centro da célula. Os íons sódio e cloreto se tocam ao longo das bordas da célula. A célula unitária contém quatro íons sódio e quatro íons cloreto, dando a estequiometria 1:1 requerida pela fórmula, NaCl.

Figure 15. Compostos iônicos com ânions que são muito maiores que cátions, como NaCl, geralmente formam uma estrutura FCC. Elas podem ser descritas pelas células da unidade FCC com cátions nos orifícios octaédricos.

A forma cúbica de sulfeto de zinco, zinco blende, também se cristaliza em uma célula da unidade FCC, como ilustrado na Figura 16. Esta estrutura contém íons de sulfeto nos pontos da malha de uma malha da FCC. (A disposição dos iões de sulfureto é idêntica à disposição dos iões de cloreto no cloreto de sódio). O raio de um íon zinco é apenas cerca de 40% do raio de um íon sulfeto, portanto esses pequenos íons Zn2+ estão localizados em furos tetraédricos alternados, ou seja, em metade dos furos tetraédricos. Há quatro íons de zinco e quatro íons de sulfeto na célula unitária, dando a fórmula empírica ZnS.

Figure 16. ZnS, sulfeto de zinco (ou zinco blende) forma uma célula da unidade FCC com íons sulfeto nos pontos da malha e íons de zinco muito menores ocupando metade dos orifícios tetraédricos da estrutura.

Uma célula da unidade de fluoreto de cálcio, como a mostrada na Figura 17, também é uma célula da unidade FCC, mas neste caso, os cátions estão localizados nos pontos da malha; íons de cálcio equivalentes estão localizados nos pontos da malha de uma malha FCC. Todos os locais tetraédricos da matriz de íons de cálcio do FCC são ocupados por íons fluoreto. Existem quatro íons de cálcio e oito íons de flúor em uma célula unitária, dando uma razão cálcio:flúor de l:2, como requerido pela fórmula química, CaF2. O exame atento da Figura 17 revelará uma matriz cúbica simples de íons fluoreto com íons cálcio em uma metade dos orifícios cúbicos. A estrutura não pode ser descrita em termos de uma malha espacial de pontos nos íons flúor porque os íons flúor não têm todos ambientes idênticos. A orientação dos quatro íons de cálcio sobre os íons fluoreto difere.

Figure 17. O fluoreto de cálcio, CaF2, forma uma célula da unidade FCC com íons de cálcio (verde) nos pontos da malha e íons de flúor (vermelho) ocupando todos os locais tetraédricos entre eles.

Cálculo dos raios iônicos

Se soubermos o comprimento da borda de uma célula unitária de um composto iônico e a posição dos íons na célula, podemos calcular os raios iônicos para os íons no composto se fizermos suposições sobre formas e contatos iônicos individuais.

Exemplo 5: Cálculo de raios iônicos

O comprimento da borda da célula unitária de LiCl (estrutura tipo NaCl-, FCC) é 0.514 nm ou 5,14 Å. Assumindo que o íon lítio é suficientemente pequeno para que os íons cloreto estejam em contato, como na Figura 15, calcular o raio iônico para o íon cloreto.

Nota: A unidade de comprimento angstrom, Å, é freqüentemente usada para representar dimensões em escala atômica e é equivalente a 10-10 m.

Mostrar solução

Na face de uma célula da unidade LiCl, os íons cloreto entram em contato entre si através da diagonal da face:

Desenhando um triângulo direito na face da célula unitária, vemos que o comprimento da diagonal é igual a quatro raios de cloreto (um raio de cada canto de cloreto e um diâmetro – o que equivale a dois raios – do íon cloreto no centro da face), portanto d = 4r. Do teorema de Pitágoras, temos:

{\a}^{2}+{\a}^{2}={\a9133>

que produz:

>esquerda(0,514 nm) ^{2}+esquerda(0.514\text{ nm}\right)^{2}={\left(4r\right)}^{2}=16{r}^{2}

Solving this gives:

r=\sqrt{\dfrac{{(0.514\text{nm})}^{2}+{(0.514\text{nm})}^{2}}{16}}=\text{0.182 nm} (1,82 Å) para um raio Cl-

Check Your Learning

O comprimento da borda da célula unitária de KCl (NaCl-like structure, FCC) é 6,28 Å. Assumindo o contacto anião-cavalo ao longo da borda da célula, calcule o raio do íon potássio. O raio do íon cloreto é 1,82 Å.

Mostrar solução

O raio do íon potássio é 1,33 Å.

É importante perceber que os valores dos raios iônicos calculados a partir do comprimento da borda das células unitárias dependem de numerosas suposições, tais como uma forma esférica perfeita para os íons, que são aproximações na melhor das hipóteses. Portanto, tais valores calculados são, em si mesmos, aproximados e as comparações não podem ser empurradas para muito longe. No entanto, este método provou ser útil para calcular raios iônicos a partir de medições experimentais, tais como determinações cristalográficas de raios X.

X-Ray Crystallography

O tamanho da célula unitária e a disposição dos átomos em um cristal podem ser determinados a partir de medições da difração dos raios X pelo cristal, denominado cristalografia de raios X. Difração é a mudança na direção de viagem experimentada por uma onda eletromagnética quando esta encontra uma barreira física cujas dimensões são comparáveis às do comprimento de onda da luz. Os raios X são radiação electromagnética com comprimentos de onda tão longos quanto a distância entre átomos vizinhos em cristais (na ordem de alguns Å).

Quando um feixe de raios X monocromáticos atinge um cristal, os seus raios são espalhados em todas as direcções pelos átomos dentro do cristal. Quando ondas dispersas viajando na mesma direção se encontram, elas sofrem interferência, um processo pelo qual as ondas se combinam para produzir um aumento ou uma diminuição na amplitude (intensidade) dependendo da extensão em que os máximos das ondas combinadas estão separados (ver Figura 18).

Figure 18. Ondas leves ocupando o mesmo espaço experimentam interferência, combinando ondas de maior (a) ou menor (b) intensidade, dependendo da separação de seus máximos e mínimos.

Quando raios X de um determinado comprimento de onda, λ, são dispersos por átomos em planos cristalinos adjacentes separados por uma distância, d, eles podem sofrer interferência construtiva quando a diferença entre as distâncias percorridas pelas duas ondas antes de sua combinação é um fator inteiro, n, do comprimento de onda. Esta condição é satisfeita quando o ângulo do feixe difratado, θ, está relacionado com o comprimento de onda e distância interatômica pela equação:

n{\lambda }=2d\text{sin}{\sin}}

Esta relação é conhecida como a equação de Bragg em homenagem a W. H. Bragg, o físico inglês que primeiro explicou este fenômeno. A figura 19 ilustra dois exemplos de ondas difratadas dos mesmos dois planos de cristal. A figura à esquerda mostra ondas difratadas no ângulo de Bragg, resultando em interferência construtiva, enquanto que a da direita mostra difração e um ângulo diferente que não satisfaz a condição de Bragg, resultando em interferência destrutiva.

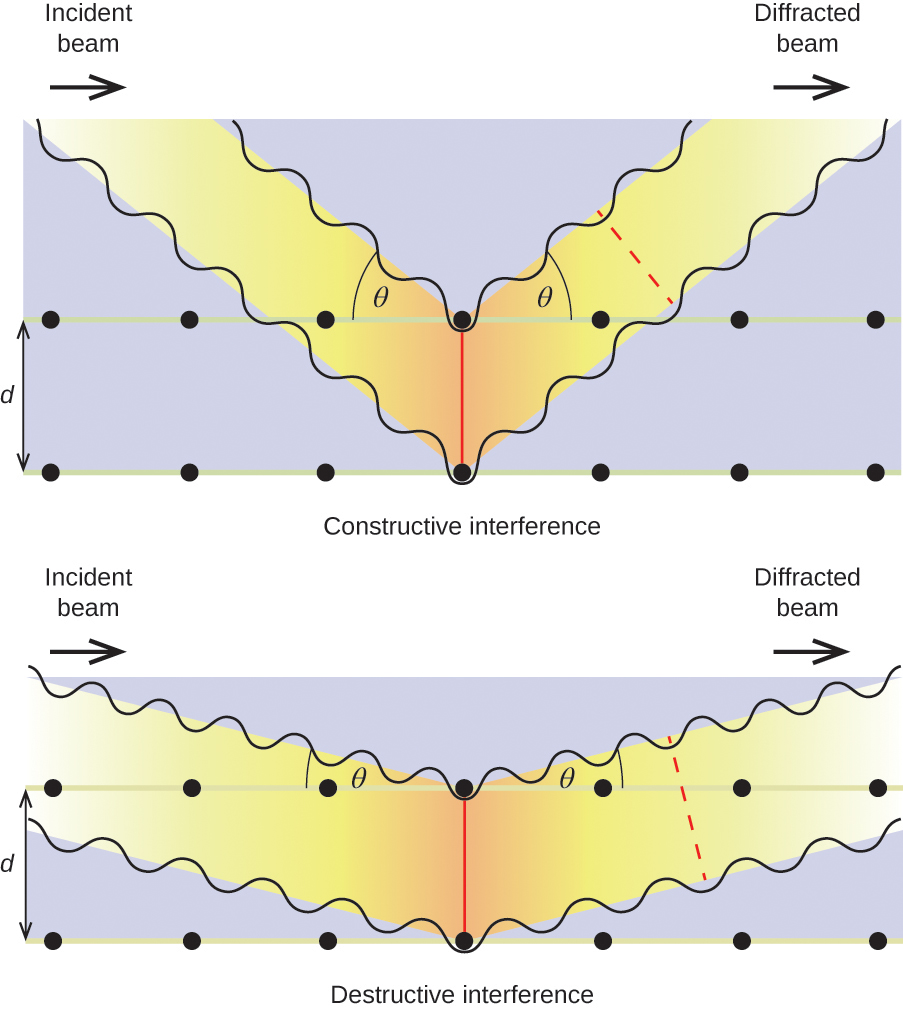
Figure 19. A difração dos raios X espalhados pelos átomos dentro de um cristal permite a determinação da distância entre os átomos. A imagem superior representa a interferência construtiva entre duas ondas dispersas e uma resultante onda difratada de alta intensidade. A imagem inferior representa a interferência destrutiva e uma onda difratada de baixa intensidade.

Um difratômetro de raios X, como o ilustrado na Figura 20, pode ser usado para medir os ângulos nos quais os raios X são difratados quando se interage com um cristal, como descrito acima. A partir dessas medidas, a equação de Bragg pode ser usada para calcular as distâncias entre átomos, como demonstrado no exemplo seguinte exercício.

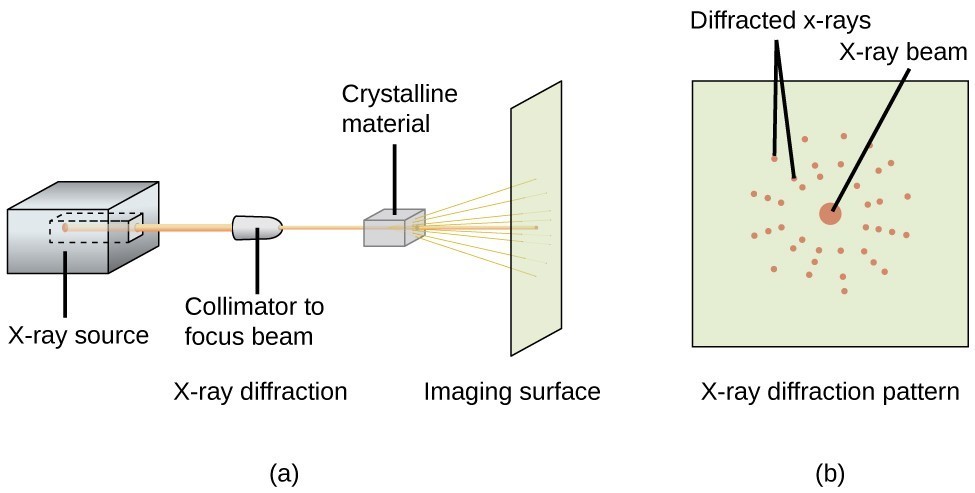
Figure 20. Em um difratômetro (a), um feixe de raios X atinge um material cristalino, produzindo um padrão de difração de raios X (b) que pode ser analisado para determinar a estrutura cristalina.

Você pode ver a transcrição para “Celebrating Crystallography – An animated adventure” aqui (abre em nova janela).

Retrato de um Químico: Cristalógrafo de raio X Rosalind Franklin

Figure 21. Esta ilustração mostra uma imagem de difração de raios X semelhante à que Franklin encontrou em sua pesquisa. (crédito: National Institutes of Health)

A descoberta da estrutura do DNA em 1953 por Francis Crick e James Watson é uma das grandes conquistas na história da ciência. Eles receberam o Prêmio Nobel de Fisiologia ou Medicina de 1962, juntamente com Maurice Wilkins, que forneceu uma prova experimental da estrutura do DNA. A química britânica Rosalind Franklin fez contribuições inestimáveis para esta monumental conquista através do seu trabalho na medição de imagens de difração de raios X do DNA. No início de sua carreira, a pesquisa de Franklin sobre a estrutura do carvão provou ser útil para o esforço de guerra britânico. Após mudar seu foco para sistemas biológicos no início dos anos 50, Franklin e o estudante de doutorado Raymond Gosling descobriram que o DNA consiste de duas formas: uma fibra longa e fina formada quando molhada (tipo “B”) e uma fibra curta e larga formada quando seca (tipo “A”). Suas imagens de difração de DNA por raios-X (Figura 21) forneceram as informações cruciais que permitiram a Watson e Crick confirmar que o DNA forma uma dupla hélice e determinar detalhes de seu tamanho e estrutura.

Franklin também realizou pesquisas pioneiras sobre vírus e o RNA que contém suas informações genéticas, descobrindo novas informações que mudaram radicalmente o corpo de conhecimento no campo. Depois de desenvolver o câncer de ovário, Franklin continuou a trabalhar até sua morte em 1958, aos 37 anos de idade. Entre muitos reconhecimentos póstuma de seu trabalho, a Chicago Medical School of Finch University of Health Sciences mudou seu nome para Rosalind Franklin University of Medicine and Science em 2004, e adotou uma imagem de sua famosa imagem de difração de raios X do DNA como seu logotipo oficial da universidade.

Glossary

Sólido cúbico centrado no corpo (BCC): estrutura cristalina que tem uma célula de unidade cúbica com pontos de malha nos cantos e no centro da célula

Célula de unidade cúbica centrada no corpo: unidade de repetição mais simples de um cristal cúbico centrado no corpo; é um cubo contendo pontos de malha em cada canto e no centro do cubo

Equação de Bragg: equação que relaciona os ângulos em que os raios X são difratados pelos átomos dentro de um cristal

número de coordenação: número de átomos mais próximos de um determinado átomo num cristal ou do átomo metálico central num complexo

empacotamento cúbico mais próximo (CCP): estrutura cristalina na qual planos de átomos ou íons próximos são empilhados como uma série de três camadas alternadas de diferentes orientações relativas (ABC)

diffraction: redireccionamento da radiação electromagnética que ocorre quando encontra uma barreira física de dimensões apropriadas

sólido cúbico centrado na face (FCC): estrutura cristalina constituída por uma célula cúbica com pontos de malha nos cantos e no centro de cada face

célula cúbica centrada na face: unidade de repetição mais simples de um cristal cúbico centrado na face; é um cubo contendo pontos de malha em cada canto e no centro de cada face

embalagem hexagonal mais próxima (HCP): estrutura cristalina na qual camadas fechadas de átomos ou íons são empilhadas como uma série de duas camadas alternadas de diferentes orientações relativas (AB)

hole: (também, interstício) espaço entre átomos dentro de um cristal

isomorfo: possuindo a mesma estrutura cristalina

furooctaédrico: espaço aberto num cristal no centro de seis partículas localizadas nos cantos de um octaedro

célula cúbica simples: (também, célula cúbica primitiva) célula unitária na estrutura cúbica simples

estrutura cúbica simples: estrutura cristalina com uma célula unitária cúbica com pontos de malha somente nos cantos

estrutura cúbica simples: todos os pontos dentro de um cristal que têm ambientes idênticos

furotetroédrico: espaço tetraédrico formado por quatro átomos ou íons em um cristal

célula unitária: menor porção de uma malha espacial que se repete em três dimensões para formar toda a malha

cristalografia de raios X: técnica experimental para determinar distâncias entre átomos em um cristal medindo os ângulos em que os raios X são difratados ao passar pelo cristal