>>
De que servem as tabelas de caracteres?
Neste ponto uma boa questão é: de que serve aprender sobre as tabelas de caracteres? A resposta simples é que a simetria e a tabela de caracteres associada de uma molécula pode ser usada para interpretar e prever muitos aspectos das espectroscopias quimicamente significativas, assim como a ligação. Vamos ilustrar isto a seguir focando nos modos vibracionais de uma molécula.
No laboratório podemos recolher dados experimentais úteis usando espectroscopia infravermelha (IR) e Raman. Estes dados podem ser comparados com o número de bandas ativas IR e/ou Raman previstas a partir da aplicação da teoria de grupos e da tabela de caracteres correta. A matemática (teoria dos grupos e álgebra matricial) por trás deste tratamento serve como uma base teórica sólida. As manipulações descritas abaixo funcionam porque todas as operações de simetria de uma molécula compreendem um grupo matemático e obedecem às regras do grupo. Como já mencionado anteriormente não precisamos dominar esta área da matemática para fazer bom uso das tabelas de caracteres.
Graus de Liberdade e Vibrações em Moléculas
Aqui discutiremos inicialmente os graus de liberdade de uma molécula simples (água). Vamos ver muito rapidamente porque é muito benéfico empregar simetria ao investigar moléculas maiores.
Para uma molécula com átomos “N” existem 3N graus de liberdade (lembre-se que vivemos num mundo tridimensional de coordenadas x, y, z). Para uma molécula não linear, 3 graus de liberdade podem ser assinados para traduções – movimento de um corpo como um todo (Tx, Ty, Tz) e 3 para rotações (Rx, Ry, Rz). Os restantes movimentos dos átomos são deslocamentos dos átomos das suas posições médias – o centro de gravidade não muda. Estas vibrações fundamentais são referidas como “modos normais”. Assim, uma molécula não-linear tem 3N-6 modos normais. Para a água o número de modos normais é 3 (3 x 3 – 6 = 3). Para moléculas lineares existem 3N-5 modos normais.
Para água, que naturalmente foi intensamente estudada sabemos que as 3 vibrações são as seguintes.
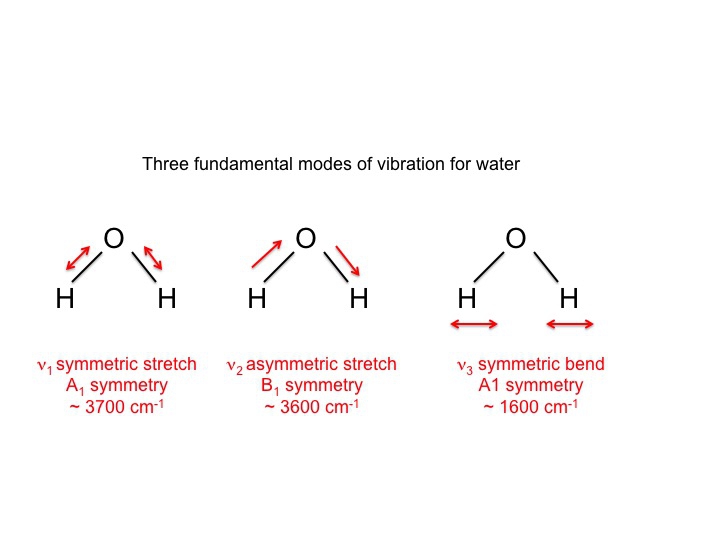
Os símbolos usados para descrever estes modos (A1, B1) são os mesmos símbolos Mulliken que encontramos na nossa discussão das tabelas de caracteres. Em outras palavras, as vibrações, que são propriedades moleculares, podem ser descritas por espécies de simetria ou por representações irredutíveis. Na verdade, grande parte da literatura envolvendo espectroscopia vibracional usa estes símbolos como uma forma abreviada de comunicar informação.
Deve ser bastante óbvio que o número de vibrações aumenta rapidamente com aumentos mesmo modestos no número de átomos na molécula. Determinar os tipos de vibrações por inspecção (como fizemos para a água) torna-se agora muito mais difícil. Por exemplo, considere os seguintes compostos:
H2O 3 átomos 3 vibrações
PH3 4 átomos 6 vibrações
CO22- 4 átomos 6 vibrações
XeF4 5 átomos 9 vibrações
B2H6 8 átomos 18 vibrações
Para o diborano (B2H6) que tem simetria D2h, a determinação da natureza e simetria das espécies de todas as 18 vibrações por inspecção seria uma tarefa assustadora. Entretanto, armado com a tabela de caracteres para D2h e conhecimento das propriedades de simetria, a tarefa de determinar as espécies de simetria de todas as vibrações é simples.
Para o caso da água poderíamos apresentar a tabela de caracteres (C2v) com as 3 vibrações (ν1, v2, v3) listadas na coluna de propriedades moleculares como mostrado abaixo. (ν = Símbolo grego “nu”)

No entanto, em geral esta abordagem é impraticável. Pegue a piridina (C5H5N), por exemplo. O grupo de pontos também é C2v mas a molécula tem 11 átomos. O número de modos fundamentais de vibração é 27 ( 3 x 11 – 6 = 27).
Neste caso teríamos de elaborar uma tabela de caracteres C2v mostrando as simetrias de todas as 27 vibrações. Por este motivo as vibrações não são normalmente incluídas nas tabelas de caracteres. Em vez disso, cabe ao usuário (você) determinar o número e tipo de vibrações (como definido por suas espécies de simetria) para quaisquer moléculas que são encontradas. Como nós fazemos isso é descrito abaixo.
Representações redutíveis
Como já foi dito anteriormente, uma das propriedades importantes das tabelas de caracteres é que as operações de simetria são membros de um grupo matemático e existem relações importantes entre elas. Em geral o mesmo pode ser dito sobre as espécies de simetria ou representações irredutíveis das propriedades moleculares. Os produtos da combinação dos caracteres de representações irredutíveis, seja por multiplicação ou adição/subtração, também obedecem às regras do grupo. As novas representações não são mais as mais simples possíveis e são chamadas de “representações redutíveis” porque elas podem ser “reduzidas” até suas partes componentes.
Por exemplo, para a água as simetrias das traduções (Tx, Ty, Tz) podem ser obtidas diretamente da tabela de caracteres C2v. Eles são A1, B1, e B2. Podemos representar todos estes três graus de liberdade através de uma representação ΓT e podemos escrever a expressão abaixo. (Γ = letra grega maiúscula “gamma”).
ΓT = A1 + B1 + B2
Sabemos que A1, B1 e B2 são apenas as notações abreviadas para as espécies de simetria (representações irredutíveis). Portanto, podemos simplesmente escrever os caracteres de ΓT adicionando os caracteres individuais para A1, B1 e B2 da tabela de caracteres C2v.
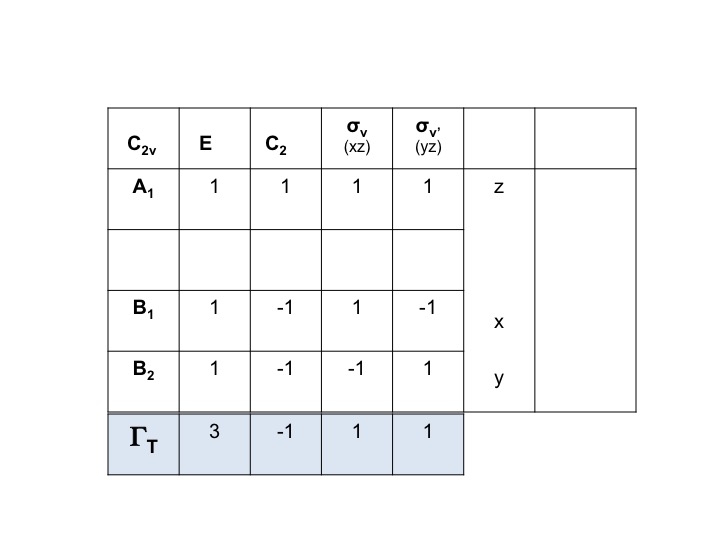
Thus ΓT = 3 -1 1 1.
Esta é uma representação redutível válida e um membro do grupo C2v.
De forma semelhante podemos escrever a representação redutível para todas as três rotações e todas as vibrações.
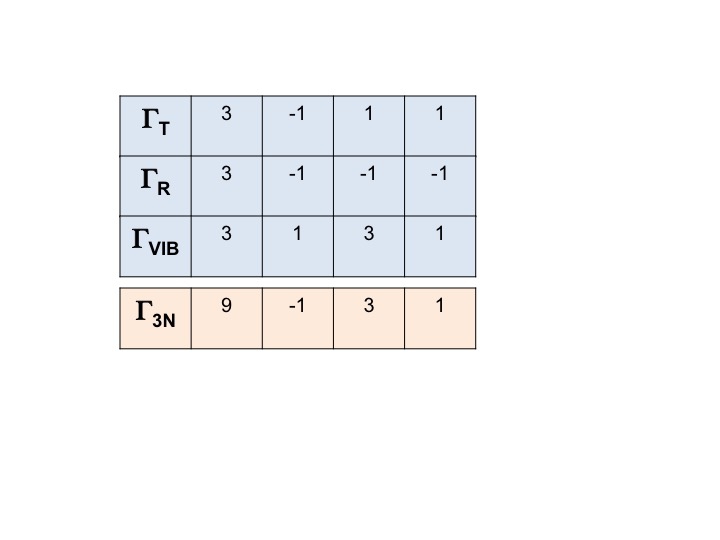
A representação para TODOS os graus de liberdade para a molécula (3N) pode ser escrita como
Γ3N = ΓT + ΓR + ΓVIB
e a representação redutível para ela é obtida pela simples soma dos caracteres para ΓT, ΓR e ΓVIB.
Γ3N = 9 -1 3 1
Faça uma nota disto – ela virá mais tarde!
Pesar de o conjunto de caracteres 9 -1 3 1 ser um membro válido do grupo C2v, não é particularmente útil quando se discute propriedades moleculares. O que é realmente necessário é a linguagem das espécies de simetria curta (símbolos Mulliken, A1, B1, etc.). Em outras palavras, queremos expressar Γ3N em termos de A1, B1, etc. A partir da informação acima pode ser facilmente mostrado pela inspecção que:
Γ3N = 3A1 +A2 + 3B1 +2B2
A boa notícia é que para outras moléculas mais complexas não temos que realizar esta tarefa pela inspecção porque:
1. Podemos facilmente gerar Γ3N como uma representação redutível para uma molécula (se conhecemos sua simetria de grupo de pontos).
2. Podemos facilmente converter a representação redutível de Γ3N na soma de suas espécies de simetria (símbolos Mulliken) usando uma fórmula “simples” conhecida como fórmula de redução.
Método geral para obter Γ3N
Passo 1
Toma a tabela de caracteres para a molécula e adiciona uma linha na parte inferior. Nesta linha, gere a representação redutível para ΓT (ou Γxyz) como fizemos acima, simplesmente adicionando os caracteres para cada operação que correspondem às propriedades moleculares para x, y e z. Para C2v já mostramos que estes são os caracteres correspondentes a A1, B1 e B2.
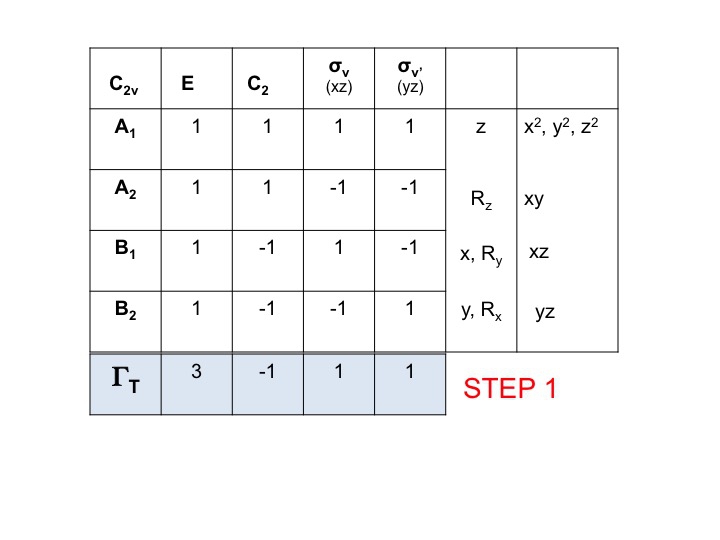
Passo 2
Adicionar outra linha abaixo de ΓT e anotar o número de átomos que NÃO MODIFICAM a sua localização durante cada operação de simetria. Aqui é onde você percebe a utilidade de um conjunto de modelos moleculares reais. Para fazer isso você também precisará saber onde estão os elementos de simetria e como as operações de simetria afetam a molécula. É claro que você já sabe como fazer isso porque estudou a notação de Schönflies e sabe como atribuir o grupo de pontos de uma molécula. A tabela de caracteres também tem todas as operações de simetria listadas por classe ao longo da linha superior.
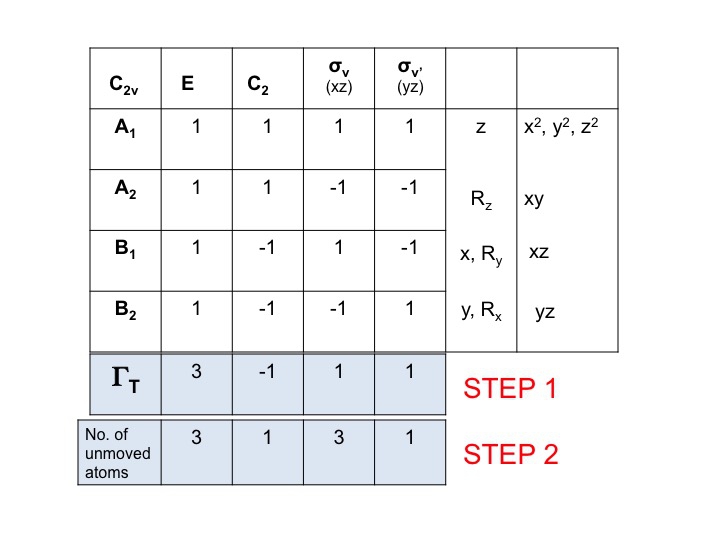
Aqui para a água (3 átomos) sob E há 3 átomos não movimentados, mas para C2 ambos os H se movem, mas como o átomo O se senta no eixo C2 ele não muda sua localização e assim registramos 1 sob a coluna C2. O novo conjunto de números gerados no passo 2 (3 1 3 1) também é uma representação redutível em C2v e obedece às regras do grupo.
Step 3
Neste passo simplesmente multiplicamos juntos os caracteres que foram gerados nos passos 1 e 2. O resultado (terceira linha) é a representação redutível para Γ3N (ou ΓTOT). É aquela simples.
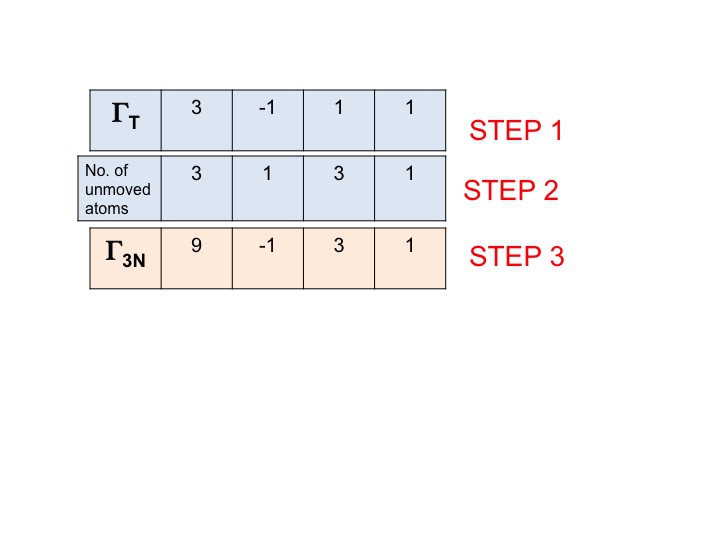
Você notará que a nova representação redutível (9 -1 1 3) é idêntica à representação para Γ3N que obtivemos anteriormente por inspeção.
Representação redutível
Para converter QUALQUER representação redutível na soma das suas representações irredutíveis (espécies de simetria ou símbolos Mulliken) usamos uma fórmula de redução:

Pode facilmente encontrar esta informação na tabela de caracteres:
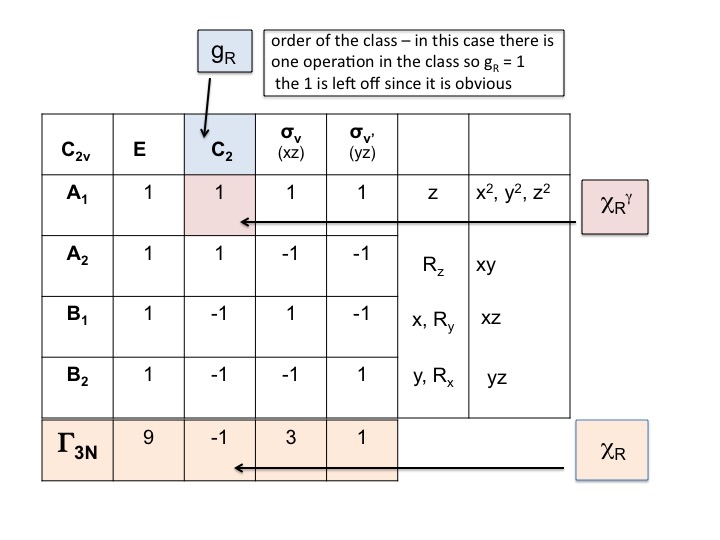
Voltar ao nosso exemplo para a água: Grupo de pontos C2v, ordem (g) = 4
A representação redutível para Γ3N = 9 -1 3 1
O número de vezes A1 aparece nesta representação é portanto
aA1 = 1/4 { 1.1.9 + 1.1. (-1) + 1.1.3 +1.1.1} = 3
so Γ3N contém 3 espécies de simetria A1. Os números das outras espécies de simetria são calculados da seguinte forma:
aA2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1).3 + 1.(-1).1 } = 1 um A2 presente
aB1 = 1/4 { 1.1.9 + 1.(-1).(-1) + 1.1.3 + 1.(-1).1} = 1 um A2 presente
aB1 = 1/4 { 1.1.9 + 1.(-1).(-1).(-1) + 1.(-1).1} = 3 3 B1 presente
aB2 = 1/4 {1.1.9 + 1.(-1)(-1)(-1) + 1.(-1).3 + 1.1.1} = 2 2 B2 presente
Podemos agora escrever Γ3N = 3A1 + A2 + 3B1 + 2B2 (exactamente o que obtivemos por “inspecção” acima. Agora podemos subtrair as espécies de simetria para as traduções e rotações e isto nos dará o número e espécies de simetria dos modos fundamentais de vibração. ΓT e ΓR podem ser obtidos diretamente da tabela de caracteres.
ΓVIB = 3A1 + A2 + 3B1 + 2B2
ΓVIB = A1 + B1 + B2
Γ3N = A2 + B1 + B2
Γ3N = ΓVIB – ΓT – ΓR = 2A1 +B1
Então os três modos normais de vibração para água têm as simetrias A1, A1 e B1.
Agora temos um método geral para determinar todos os modos fundamentais de vibração de uma molécula e expressar estes modos na linguagem abreviada dos símbolos Mulliken. Este é um dos exercícios que você será testado no Exame 1. A melhor maneira de se tornar confiante com este método é praticar o máximo de exemplos possíveis!
Next: Regras de selecção