Trójkąt pitagorejski to trójka dodatnich liczb całkowitych , i takich, że istnieje trójkąt prosty o nogach i przeciwprostokątnej . Z twierdzenia pitagorejskiego wynika, że jest to równoważne znalezieniu dodatnich liczb całkowitych , i spełniających warunki

Najmniejszym i najbardziej znanym trójkątem pitagorejskim jest . Trójkąt prosty o takich długościach boków jest czasem nazywany trójkątem 3, 4, 5.

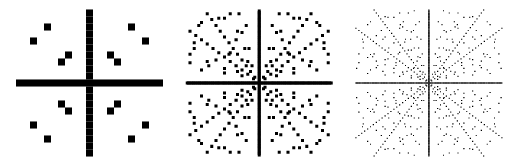
Plany punktów w płaszczyźnie takich, że jest trójką pitagorejską są pokazane powyżej dla kolejno większych granic. Działki te zawierają ujemne wartości i , są więc symetryczne zarówno względem osi x, jak i y.

Podobnie, działki punktów w płaszczyźnie takich, że jest trójką pitagorejską są pokazane powyżej dla kolejno większych granic.

Zwykło się rozważać tylko prymitywne trójki pitagorejskie (zwane też trójkami „zredukowanymi”), w których i są względnie pierwsze, gdyż inne rozwiązania można wygenerować trywialnie z prymitywnych. Prymitywne trójki są zilustrowane powyżej i można od razu zauważyć, że linie radialne odpowiadające prymitywnym trójkom w oryginalnym wykresie są nieobecne na tym rysunku. Dla prymitywnych rozwiązań, jedno z lub musi być parzyste, a drugie nieparzyste (Shanks 1993, s. 141), przy czym zawsze jest nieparzyste.

Dodatkowo, jeden bok każdej trójki pitagorejskiej jest podzielny przez 3, inny przez 4, a jeszcze inny przez 5. Jeden bok może mieć dwa z tych dzielników, jak w (8, 15, 17), (7, 24, 25) i (20, 21, 29), a nawet wszystkie trzy, jak w (11, 60, 61).

Dając trójkę prymitywną , otrzymujemy trzy nowe trójki prymitywne z

			(2)
			(3)
			(4)

gdzie

.

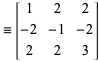		(5)
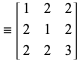		(6)
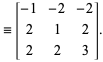		(7)

Hall (1970) i Roberts (1977) dowodzą, że jest prymitywną trójką pitagorejską, jeśli

gdzie jest skończonym iloczynem macierzy , , . Wynika stąd, że każda prymitywna trójka pitagorejska musi być członkiem nieskończonej macierzy

Pythagoras i Babilończycy podali wzór na generowanie (niekoniecznie prymitywnych) trójek jako

dla , co generuje zbiór odrębnych trójek nie zawierający ani wszystkich trójek prymitywnych, ani wszystkich trójek imprimitywnych (i gdzie w szczególnym przypadku , ).

Wcześni Grecy podali

gdzie i są względnie pierwsze i o przeciwnej parzystości (Shanks 1993, s. 141), co generuje zbiór odrębnych trójek zawierający właśnie te prymitywne trójki (po odpowiednim posortowaniu i ).

Pozwólmy być liczbą Fibonacciego. Wtedy

generuje wyraźne trójki pitagorejskie (Dujella 1995), choć nie wyczerpująco ani dla trójek prymitywnych, ani imprimitywnych. Ogólniej, zaczynając od dodatnich liczb całkowitych , i konstruując ciąg podobny do ciągu Fibonacciego o wyrazach , , , , , … generuje rozłączne trójki pitagorejskie

(Horadam 1961), gdzie

(Beiler 1966, s. 116). Zauważmy, że iff jest pierwsza lub dwa razy pierwsza. Kilka liczb pierwszych dla , 2, … to 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 4, 1, … (OEIS A046079).

Aby znaleźć liczbę sposobów , na jakie liczba może być przeciwprostokątną prymitywnego trójkąta prostego, zapisz jej faktoryzację jako

gdzie s jest postaci , a s jest postaci . Liczba możliwych prymitywnych trójkątów prostych wynosi wtedy

Na przykład, ponieważ

.

			(27)
			(28)

Wartości dla , 2, … wynoszą 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, …. (OEIS A024362). Pierwsze kilka liczb pierwszych w postaci to 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, … (OEIS A002144), więc najmniejsze długości boków, które są przeciwprostokątnymi 1, 2, 4, 8, 16, … trójkątów prostokątnych to 5, 65, 1105, 32045, 1185665, 48612265, … (OEIS A006278).

Liczba możliwych prymitywnych lub nieprymitywnych trójkątów prostokątnych mających jako przeciwprostokątną wynosi

.

			(29)
			(30)

(poprawiając literówkę z Beiler 1966, p. 117, w którym podano, że wzór ten podaje tylko liczbę rozwiązań nieprymitywnych), gdzie jest funkcją sumy kwadratów. Na przykład, istnieją cztery różne trójkąty całkowite o przeciwprostokątnej 65, ponieważ

Liczby pierwsze dla , 2, … to 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, …. (OEIS A046080). Najmniejsze hipotensy mające różnych trójek to 1, 5, 25, 125, 65, 3125, … (OEIS A006339). Poniższa tabela podaje hipotensy, dla których istnieje dokładnie różnych trójkątów całkowitych prostych dla , 1, …, 5.

	OEIS	hipotenusy, dla których istnieje różnych trójkątów całkowitych
0	A004144	1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, …
1	A084645	5, 10, 13, 15, 17, 20, 26, 29, 30, 34, 35, …
2	A084646	25, 50, 75, 100, 150, 169, 175, 200, 225, …
3	A084647	125, 250, 375, 500, 750, 875, 1000, 1125, 1375, …
4	A084648	65, 85, 130, 145, 170, 185, 195, 205, 221, 255, …
5	A084649	3125, 6250, 9375, 12500, 18750, 21875, 25000, …

Wobec tego całkowita liczba sposobów, na jakie może być nogą lub przeciwprostokątną trójkąta prostokątnego, jest dana przez

Wartości dla , 2, … wynoszą 0, 0, 1, 1, 2, 1, 1, 1, 2, 2, 2, 1, 4, 2, 1, 5, 3, …. (OEIS A046081). Najmniejszymi liczbami , które mogą być bokami ogólnych trójkątów prostokątnych dla , 2, … są 3, 5, 16, 12, 15, 125, 24, 40, … (OEIS A006593; Beiler 1966, s. 114).

Istnieje 50 trójkątów pitagorejskich o hipotensjach mniejszych od 100, z których pierwsze kilka, uporządkowane według rosnących , to (3, 4, 5), (6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083, A046084, i A009000).

Spośród nich, tylko 16 jest prymitywnymi trójkami o przeciwprostokątnej mniejszej niż 100: (3, 4,5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65), (16, 63, 65), (48, 55, 73), (36, 77, 85), (13, 84, 85), (39, 80, 89), i (65, 72, 97) (OEIS A046086, A046087, i A020882).

Let the number of triples with hypotenuse be denoted , the number of triples with hypotenuse be denoted , and the number of primitive triples less than be denoted . Następnie w poniższej tabeli zestawiono wartości dla potęg 10.

	OEIS	, , …
	A101929	1, 50, 878, 12467, …
	A101930	2, 52, 881, 12471, …
	A101931	1, 16, 158, 1593, ….

Lehmer (1900) udowodnił, że liczba rozwiązań prymitywnych o hipotensji mniejszej niż spełnia

(OEIS A086201).

Intradycje kilku pierwszych prymitywnych trójkątów pitagorejskich uporządkowanych rosnąco są dane przez 1, 2, 3, 3, 6, 5, 4, 10, 5, …. (OEIS A014498).

Istnieje ogólna metoda otrzymywania trójek trójkątów pitagorejskich o równych powierzchniach. Weźmy trzy zbiory generatorów jako

.

.

.

.

			(34)
			(35)
			(36)
			(37)
			(38)
			(39)

Wtedy trójkąt prosty generowany przez każdą trójkę () ma pole wspólne

(Beiler 1966, s. 126-127). Jedyne ekstremum tej funkcji występuje w punkcie . Ponieważ dla , to najmniejszy obszar wspólny dla trzech nieprostokątnych trójkątów prostych jest dany przez , co daje obszar 840 i odpowiada trójkątom (24, 70, 74), (40, 42, 58) i (15, 112, 113) (Beiler 1966, s. 126).

Trójkąty proste, których pola składają się z jednej cyfry, to (pole 6) i (pole 666666; Wells 1986, s. 89).

W 1643 roku Fermat rzucił Mersenne’owi wyzwanie znalezienia trójkąta pitagorejskiego, którego przeciwprostokątna i suma nóg byłyby kwadratami. Fermat znalazł najmniejsze takie rozwiązanie:

.

			(41)
			(42)
			(43)

z

.

			(44)
			(45)

Pokrewnym problemem jest określenie, czy określona liczba całkowita może być polem trójkąta prostokątnego o racjonalnych bokach. 1, 2, 3 i 4 nie są polami żadnych trójkątów prostokątnych o racjonalnych bokach, ale 5 jest (3/2, 20/3, 41/6), podobnie jak 6 (3, 4, 5). Rozwiązanie problemu dotyczy krzywej eliptycznej

Rozwiązanie (, , ) istnieje, jeśli (46) ma racjonalne rozwiązanie, w którym to przypadku

			(47)
			(48)

(Koblitz 1993). Nie jest znana ogólna metoda pozwalająca określić, czy istnieje rozwiązanie dla dowolnych , ale technika opracowana przez J. Tunnella w 1983 roku pozwala wykluczyć pewne wartości (Cipra 1996).

.