Jeden z rosnących obszarów zainteresowania naukowców badających znaczenie, władzę lub wpływy wśród podmiotów nazywany jest Teorią Grafów. Korzenie teorii grafu rozpoczął się w 1736 roku, kiedy matematyk Carl Ehler wprowadził Leonhard Euler do Mosty Konigsberg problem.
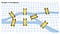
Mosty Konigsberg problem jest oparty w byłym niemieckim mieście Konigsberg, który leży po obu stronach rzeki Pregel. W jego centrum znajdowały się dwie duże wyspy, które były połączone ze sobą i z brzegami rzeki siedmioma mostami. Carl Ehler miał obsesję na punkcie znalezienia trasy, która pozwoliłaby mu przejść przez każdy z siedmiu mostów, nie przechodząc przez żaden z nich więcej niż raz. Ehler skontaktował się z Leonhardem Eulerem, szwajcarskim matematykiem. Euler potwierdził hipotezę Ehlera, że problem nie ma rozwiązania, a wyjaśnienie Eulera poinformował nowy paradygmat matematyczny o nazwie Geometria pozycji.
Nowy paradygmat geometrii Eulera stwierdził, że lokalizacja mostów nie ma znaczenia. Zamiast tego problem można uprościć, zamieniając każdy most w punkt (węzeł) z liniami (krawędziami) reprezentującymi połączenia między nimi. Ta praktyka używania węzłów i krawędzi jest obecnie znana jako teoria grafów.
Więcej o problemie mostów w Królewcu można przeczytać tutaj.
Początkowo teoria grafów nie służyła zbytnio do rozwiązywania problemów i nie była wysoko ceniona przez matematyków. Jednak współczesna moc obliczeniowa umożliwiająca przetwarzanie dużych permutacji sprawiła, że zasady Teorii Grafów stały się bardziej praktyczne. Ten artykuł uczy stosowania zasad Teorii Grafu w analizie opartej na języku Python.


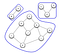
Nie wszystkie sieci w systemie Graph są ze sobą połączone. To rozłączenie następuje, gdy tworzą się komponenty. Jak pokazano na poniższym wykresie, komponent jest utworzony tylko wtedy, gdy każdy węzeł ma ścieżkę do innych węzłów.
Zastosowana teoria grafów w Pythonie
W Pythonie pakiet networkx jest często używany do stosowanej teorii grafów znanej również jako analiza sieci. Pakiet posiada przydatną funkcjonalność do szybkiego podsumowania charakterystyki grafu. Możesz przejrzeć poniższe kroki i podążać za nimi, gdy tworzymy graf i rozumiemy jego skład.
Najpierw poniższy kod tworzy pusty obiekt grafu P. Następne kroki dodają węzły i opisują krawędzie.
Argumenty takie jak <object>.nodes() lub <object>.edges() są szybkimi sposobami wyświetlenia wszystkich węzłów i krawędzi systemu grafu.
print(P.nodes())print(P.edges())
W końcu, nx.draw jest używany do wizualizacji sieci.
%matplotlib inline
import matplotlib.pyplot as plt
nx.draw(P, with_labels = True)
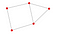
Ćwiczenia 1:
Teraz, gdy podstawowe pojęcia grafów zostały omówione, poniższe ćwiczenia są dobrą metodą na przećwiczenie:
- Ile węzłów znajduje się w powyższym grafie?
- Ile krawędzi jest w powyższym grafie?
- Jaka jest geodezyjna dla E i C?
- Czy w grafie jest więcej niż 1 składnik?
Używanie rzeczywistych danych
W poniższym ćwiczeniu zostaną użyte dane dotyczące lotów w Stanach Zjednoczonych w 2015 roku. Zbiór danych zawiera lotniska początkowe i docelowe, a także atrybuty opisujące lot, w tym czas lotu i opóźnienia (związane z pogodą, bezpieczeństwem lub liniami lotniczymi).
Ponieważ zbiór danych jest duży, ćwiczenie skupi się na lotach rozpoczynających się z lotnisk w rejonie Los Angeles (Los Angeles (LAX), Burbank (BUR), Orange County (SNA) i San Bernardino County (ONT)). Ponadto skupimy się na przeglądaniu lotów, które przypominają mój harmonogram podróży w Deloitte – wyloty w niedziele i powroty w czwartki.
Ponieważ mamy już dane dotyczące miejsca początkowego i docelowego, **** pola ORIGIN_AIRPORT i DESTINATION_AIRPORT posłużą jako pola źródłowe dla węzłów i krawędzi – nie ma potrzeby tworzenia węzłów ani krawędzi, jak to miało miejsce w pierwszym ćwiczeniu. Gdy węzły zostaną zdefiniowane, <object>.edges() dostarczy wszystkie relacje parami między nimi. Na koniec, nx.draw pomoże utworzyć wykres do krawędzi.

FG.edges()

nx.draw(FG, with_labels = True)

W powyższych danych wyjściowych, węzły są oznaczone kodami lotnisk. Wszystkie krawędzie prowadzą do jednego z czterech lotnisk w rejonie Los Angeles, ponieważ tylko te cztery zostały wybrane do tego ćwiczenia. Los Angeles International (LAX) jest największym lotniskiem spośród tych czterech i wykres wyraźnie pokazuje, że wiele miast jest dostępnych tylko z LAX, a nie z innych mniejszych lotnisk. Pokazuje to powiązanie lub stopień centralności LAX. W networkx, nx.algorithms.degree_centrality(<object>) ****is używany do znalezienia centralności każdego węzła w systemie grafu.
# Calculating the centrality of each of the airports
nx.algorithms.degree_centrality(FG)
Możemy pójść bardziej granularnie i użyć krótkiej 'pętli for’ do wytworzenia krawędzi pomiędzy dwoma obszarami zainteresowania. Na przykład poniższy kod jest używany do znalezienia wszystkich możliwych lotów z hrabstwa San Bernardino (ONT) do Newark (EWR) w niedzielę lub czwartek.
Wśród kilku opcji lotów między hrabstwem San Bernardino a Newark można użyć nx.dijkstra_path do znalezienia ścieżki euklidesowej (lub najkrótszej ścieżki).
#Finding the dijkstra path
djk_path = nx.dijkstra_path(FG, source='ONT', target='EWR')
djk_path
Ćwiczenia 2:
- Wytwórz następujący graf, używając
nx.draw(). Uwaga: Twoja sieć może nie wyglądać dokładnie tak samo, ale ścieżki, krawędzie i węzły powinny pasować do sieci poniżej. - Wydrukuj wszystkie krawędzie.
- Jaka jest najkrótsza ścieżka z L do F?

.