W XVII, a zwłaszcza XVIII w, kierowani zarówno chęcią zrozumienia natury, jak i poszukiwaniem balonów, w których mogliby latać (Rysunek 1), liczni naukowcy ustalili zależności pomiędzy makroskopowymi właściwościami fizycznymi gazów, czyli ciśnieniem, objętością, temperaturą i ilością gazu. Chociaż ich pomiary nie były precyzyjne według dzisiejszych standardów, byli oni w stanie określić matematyczne zależności pomiędzy parami tych zmiennych (np. ciśnienie i temperatura, ciśnienie i objętość), które obowiązują dla gazu idealnego – hipotetycznej konstrukcji, którą rzeczywiste gazy przybliżają w pewnych warunkach. Ostatecznie, te poszczególne prawa zostały połączone w jedno równanie – prawo gazu idealnego – które odnosi się do ilości gazu dla gazów i jest dość dokładne dla niskich ciśnień i umiarkowanych temperatur. Rozważymy kluczowe zmiany w poszczególnych zależnościach (ze względów pedagogicznych nie do końca w porządku historycznym), a następnie połączymy je w prawo gazu idealnego.

Rysunek 1. W 1783 r. odbył się pierwszy (a) lot balonem wypełnionym wodorem, (b) załogowy lot balonem na ogrzane powietrze i (c) załogowy lot balonem wypełnionym wodorem. Gdy balon wypełniony wodorem przedstawiony w (a) wylądował, przestraszeni mieszkańcy Gonesse zniszczyli go podobno widłami i nożami. Start tego ostatniego oglądało podobno 400 000 osób w Paryżu.

Ciśnienie i temperatura: Gay-Lussac’s Law

Wyobraź sobie, że wypełniasz sztywny pojemnik przymocowany do manometru gazem, a następnie uszczelniasz pojemnik tak, aby żaden gaz nie mógł się wydostać. Jeśli pojemnik jest schładzany, gaz w nim zawarty również staje się zimniejszy i obserwuje się spadek jego ciśnienia. Ponieważ pojemnik jest sztywny i szczelnie zamknięty, zarówno objętość, jak i liczba moli gazu pozostają stałe. Jeśli natomiast ogrzejemy kulę, to gaz w jej wnętrzu staje się cieplejszy (rysunek 2), a ciśnienie rośnie.

Rysunek 2. Wpływ temperatury na ciśnienie gazu: Gdy płyta grzejna jest wyłączona, ciśnienie gazu w kuli jest stosunkowo niskie. W miarę ogrzewania gazu ciśnienie gazu w kuli rośnie.

Tę zależność między temperaturą a ciśnieniem obserwuje się dla dowolnej próbki gazu zamkniętej w stałej objętości. Przykład danych doświadczalnych ciśnienie-temperatura jest pokazany dla próbki powietrza w tych warunkach na rysunku 3. Stwierdzamy, że temperatura i ciśnienie są liniowo powiązane, a jeśli temperatura jest w skali kelwina, to P i T są wprost proporcjonalne (ponownie, gdy objętość i mole gazu są utrzymywane na stałym poziomie); jeśli temperatura w skali kelwina wzrasta o pewien czynnik, to ciśnienie gazu wzrasta o ten sam czynnik.

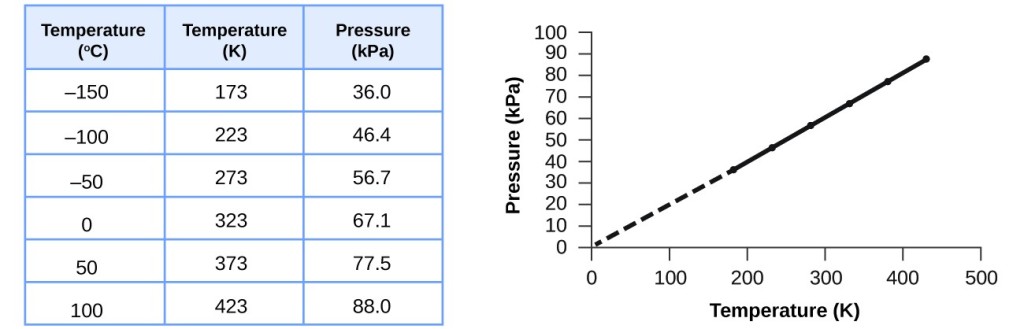
Rysunek 3. Dla stałej objętości i ilości powietrza, ciśnienie i temperatura są wprost proporcjonalne, pod warunkiem, że temperatura podana jest w kelwinach. (Pomiary nie mogą być wykonywane w niższych temperaturach z powodu kondensacji gazu). Kiedy linia ta jest ekstrapolowana do niższych ciśnień, osiąga ciśnienie 0 w temperaturze -273 °C, która jest 0 w skali kelwinów i najniższą możliwą temperaturą, zwaną zerem bezwzględnym.

Guillaume Amontons jako pierwszy empirycznie ustalił związek między ciśnieniem a temperaturą gazu (~1700), a Joseph Louis Gay-Lussac określił ten związek bardziej precyzyjnie (~1800). Z tego powodu, zależność P-T dla gazów jest znana jako prawo Gay-Lussaca lub prawo Amontona. Pod każdą z tych nazw stwierdza ono, że ciśnienie danej ilości gazu jest wprost proporcjonalne do jego temperatury w skali kelwinów, gdy objętość jest utrzymywana na stałym poziomie. Matematycznie można to zapisać następująco:

Duża P=czas T

Duża P=czas T

Duża P=kczas T

gdzie ∝ oznacza „jest proporcjonalne do”, a k jest stałą proporcjonalności, która zależy od tożsamości, ilości i objętości gazu.

Wielkość = =frac{{P}_{1}}{{T}_{1}}= =frac{{P}_{2}}{{T}_{2}}}

Równanie to jest przydatne do obliczeń ciśnienie-temperatura dla gazu zamkniętego w stałej objętości. Zauważ, że temperatury muszą być w skali kelwina dla wszelkich obliczeń związanych z prawem gazowym (0 w skali kelwina i najniższa możliwa temperatura nazywana jest zerem bezwzględnym). (Należy również pamiętać, że istnieją co najmniej trzy sposoby opisania, jak zmienia się ciśnienie gazu wraz ze zmianą jego temperatury: Możemy użyć tabeli wartości, wykresu, lub równania matematycznego.)

Objętość i temperatura: Charles’s Law

Jeśli napełnimy balon powietrzem i zamkniemy go, balon zawiera określoną ilość powietrza przy ciśnieniu atmosferycznym, powiedzmy 1 atm. Jeśli włożymy balon do lodówki, gaz w nim się oziębi i balon się skurczy (choć zarówno ilość gazu, jak i jego ciśnienie pozostają niezmienne). Jeśli sprawimy, że balon będzie bardzo zimny, bardzo się skurczy, a po ogrzaniu ponownie się rozszerzy.

Te przykłady wpływu temperatury na objętość danej ilości zamkniętego gazu przy stałym ciśnieniu są prawdziwe w ogólności: Objętość rośnie wraz ze wzrostem temperatury, a maleje wraz ze spadkiem temperatury. Dane objętościowo-temperaturowe dla próbki 1-molowego gazu metanu w ciśnieniu 1 atm są zestawione i przedstawione na wykresie na rysunku 4.

Rysunek 4. Objętość i temperatura są liniowo zależne dla 1 mola metanu przy stałym ciśnieniu 1 atm. Jeśli temperatura podana jest w kelwinach, objętość i temperatura są wprost proporcjonalne. Linia zatrzymuje się w 111 K, ponieważ metan skrapla się w tej temperaturze; po ekstrapolacji przecina początek wykresu, reprezentując temperaturę zera bezwzględnego.

Zależność między objętością i temperaturą danej ilości gazu przy stałym ciśnieniu jest znana jako prawo Charlesa w uznaniu francuskiego naukowca i pioniera lotów balonowych Jacques’a Alexandre’a Césara Charlesa. Prawo Charlesa stwierdza, że objętość danej ilości gazu jest wprost proporcjonalna do jego temperatury w skali kelwinów, gdy ciśnienie jest utrzymywane na stałym poziomie.

Matematycznie można to zapisać jako:

Wielkość V=stała T

Wielkość V=stała T

Wielkość V=kstała T

z tym, że k jest stałą proporcjonalności, która zależy od ilości i ciśnienia gazu.

Wielkość V=k}{{V}_{1}}{{T}_{1}}}

Objętość i ciśnienie: Prawo Boyle’a

Jeśli częściowo wypełnimy szczelną strzykawkę powietrzem, to strzykawka zawiera określoną ilość powietrza w stałej temperaturze, powiedzmy 25°C. Jeśli powoli wciśniemy tłok, utrzymując stałą temperaturę, gaz w strzykawce zostanie ściśnięty do mniejszej objętości, a jego ciśnienie wzrośnie; jeśli wyciągniemy tłok, objętość wzrośnie, a ciśnienie spadnie. Ten przykład wpływu objętości na ciśnienie danej ilości zamkniętego gazu jest prawdziwy w ogólności. Zmniejszanie objętości zamkniętego gazu powoduje wzrost jego ciśnienia, a zwiększanie objętości powoduje spadek ciśnienia. W rzeczywistości, jeśli objętość wzrasta o pewien czynnik, ciśnienie spada o ten sam czynnik i odwrotnie. Dane dotyczące objętości i ciśnienia dla próbki powietrza w temperaturze pokojowej przedstawiono na wykresie na rysunku 5.

Rysunek 5. Gdy gaz zajmuje mniejszą objętość, wywiera większe ciśnienie; gdy zajmuje większą objętość, wywiera mniejsze ciśnienie (przy założeniu, że ilość gazu i temperatura nie ulegają zmianie). Ponieważ P i V są odwrotnie proporcjonalne, wykres zależności 1/P od V jest liniowy.

W przeciwieństwie do zależności P-T i V-T, ciśnienie i objętość nie są do siebie wprost proporcjonalne. Zamiast tego, P i V wykazują odwrotną proporcjonalność: Zwiększenie ciśnienia powoduje zmniejszenie objętości gazu. Matematycznie można to zapisać:

duże P lub }P=kdot 1 lub }P=kdot V lub }{P}_{1}{V}_{1}={P}_{2}{V}_{2}

przy czym k jest stałą. Graficznie, zależność ta jest przedstawiona za pomocą linii prostej, która powstaje po wykreśleniu odwrotności ciśnienia (V) w stosunku do objętości (V) lub odwrotności objętości (V) w stosunku do ciśnienia (V). Wykresy z zakrzywionymi liniami są trudne do dokładnego odczytania przy niskich lub wysokich wartościach zmiennych i trudniej je wykorzystać do dopasowania teoretycznych równań i parametrów do danych eksperymentalnych. Z tych powodów naukowcy często starają się znaleźć sposób na „linearyzację” swoich danych. Jeśli wykreślimy P względem V, otrzymamy hiperbolę (patrz Rysunek 6).

Zależność pomiędzy objętością i ciśnieniem danej ilości gazu w stałej temperaturze została po raz pierwszy opublikowana przez angielskiego filozofa przyrody Roberta Boyle’a ponad 300 lat temu. Jest ona podsumowana w stwierdzeniu znanym obecnie jako prawo Boyle’a: Objętość danej ilości gazu utrzymywanego w stałej temperaturze jest odwrotnie proporcjonalna do ciśnienia, pod którym jest mierzona.

Chemistry in Action: Breathing and Boyle’s Law

Co robisz około 20 razy na minutę przez całe życie, bez przerwy, a często nawet nie zdając sobie z tego sprawy? Odpowiedź to oczywiście oddychanie, czyli oddychanie. Jak to działa? Okazuje się, że zastosowanie mają tu prawa gazowe. Twoje płuca pobierają gaz potrzebny organizmowi (tlen) i pozbywają się gazów odpadowych (dwutlenek węgla). Płuca zbudowane są z gąbczastej, rozciągliwej tkanki, która rozszerza się i kurczy podczas oddychania. Podczas wdechu przepona i mięśnie międzyżebrowe (mięśnie między żebrami) kurczą się, rozszerzając jamę klatki piersiowej i zwiększając objętość płuc. Wzrost objętości prowadzi do spadku ciśnienia (prawo Boyle’a). Powoduje to przepływ powietrza do płuc (z wysokiego ciśnienia do niskiego). Podczas wydechu proces ten ulega odwróceniu: Przepona i mięśnie żebrowe rozluźniają się, jama klatki piersiowej kurczy się, a objętość płuc zmniejsza się, powodując wzrost ciśnienia (ponownie prawo Boyle’a) i powietrze wypływa z płuc (z wysokiego ciśnienia do niskiego). Następnie wdychamy i wydychamy powietrze ponownie, powtarzając ten cykl prawa Boyle’a do końca życia (ryc. 7).

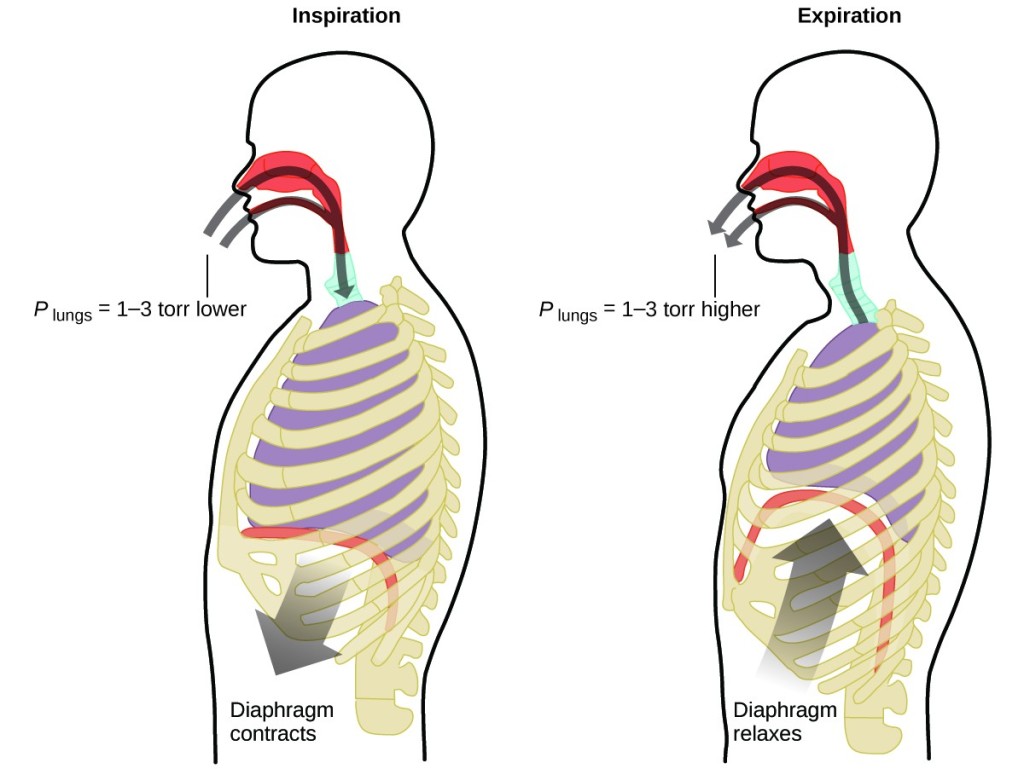
Ryc. 7. Oddychanie występuje, ponieważ rozszerzanie i kurczenie się objętości płuc powoduje powstawanie niewielkich różnic ciśnienia między płucami a otoczeniem, powodując wciąganie powietrza do płuc i wypychanie go z nich.

Mole gazu i objętość: Avogadro’s Law

Włoski naukowiec Amedeo Avogadro w 1811 roku wysunął hipotezę wyjaśniającą zachowanie gazów, stwierdzając, że jednakowe objętości wszystkich gazów, mierzone w tych samych warunkach temperatury i ciśnienia, zawierają taką samą liczbę cząsteczek. Z czasem zależność ta została poparta wieloma obserwacjami eksperymentalnymi i wyrażona prawem Avogadro: Dla gazu zamkniętego objętość (V) i liczba moli (n) są wprost proporcjonalne, jeśli zarówno ciśnienie, jak i temperatura pozostają stałe.

W formie równania zapisuje się to jako:

V=krotność n& \tekst{lub}& V=krotność n& \tekst{lub}&. \frac{{V}_{1}}{{n}_{1}}= \frac{{V}_{2}}{{n}}} \end{array}

Zależności matematyczne można również wyznaczyć dla innych par zmiennych, takich jak P versus n, i n versus T.

Odwiedź ten interaktywny link do symulacji PhET, aby zbadać zależności pomiędzy ciśnieniem, objętością, temperaturą i ilością gazu. Użyj symulacji, aby zbadać wpływ zmiany jednego parametru na inny przy zachowaniu stałych pozostałych parametrów (jak opisano w poprzednich częściach dotyczących różnych praw gazowych).

Słownik

Zero bezwzględne: temperatura, w której objętość gazu byłaby równa zeru zgodnie z prawem Charlesa.

Prawo Avogadro: objętość gazu w stałej temperaturze i pod stałym ciśnieniem jest proporcjonalna do liczby cząsteczek gazu

Prawo Boyle’a: objętość danej liczby moli gazu utrzymywanego w stałej temperaturze jest odwrotnie proporcjonalna do ciśnienia, pod jakim jest mierzona

Prawo Charlesa: objętość danej liczby moli gazu jest wprost proporcjonalna do jego temperatury kelwinowskiej, gdy ciśnienie jest utrzymywane na stałym poziomie

Prawo Gay-Lussaca: (także prawo Amontona) ciśnienie danej liczby moli gazu jest wprost proporcjonalne do jego temperatury kelwinowskiej, gdy objętość jest utrzymywana na stałym poziomie

.