Chemia dla majorów

5 sierpnia, 2021
| Brak komentarzy

Wyniki nauczania

  • Opisać rozmieszczenie atomów i jonów w strukturach krystalicznych
  • Obliczyć promienie jonowe przy użyciu wymiarów komórek jednostkowych
  • Wyjaśnić zastosowanie pomiarów dyfrakcji promieni X-dyfrakcji promieni X w określaniu struktur krystalicznych

Ponad 90% naturalnie występujących i wytworzonych przez człowieka ciał stałych to ciała krystaliczne. Większość ciał stałych tworzy się z regularnym układem ich cząsteczek, ponieważ ogólne atrakcyjne oddziaływania między cząsteczkami są zmaksymalizowane, a całkowita energia międzycząsteczkowa jest zminimalizowana, gdy cząsteczki pakują się w najbardziej efektywny sposób. Regularny układ na poziomie atomowym jest często odzwierciedlany na poziomie makroskopowym. W tym module poznamy niektóre szczegóły dotyczące struktur metalicznych i jonowych krystalicznych ciał stałych i dowiemy się, jak te struktury są określane doświadczalnie.

Struktury metali

Naszą dyskusję o krystalicznych ciałach stałych rozpoczniemy od rozważenia metali elementarnych, które są stosunkowo proste, ponieważ każdy z nich zawiera tylko jeden rodzaj atomu. Czysty metal jest krystalicznym ciałem stałym z atomami metalu upakowanymi blisko siebie w powtarzający się wzór. Niektóre z właściwości metali w ogóle, takie jak ich ciągliwość i plastyczność, są w dużej mierze spowodowane posiadaniem identycznych atomów ułożonych w regularny wzór. Różne właściwości jednego metalu w porównaniu z innym zależą częściowo od wielkości atomów i specyfiki ich przestrzennego rozmieszczenia. Zbadamy podobieństwa i różnice pomiędzy czterema najbardziej powszechnymi geometriami kryształów metali w następnych rozdziałach.

Komórki jednostkowe metali

Struktura ciała stałego krystalicznego, niezależnie od tego, czy jest to metal, czy nie, jest najlepiej opisana poprzez rozważenie jego najprostszej powtarzającej się jednostki, która jest określana jako jego komórka jednostkowa. Komórka składa się z punktów kratowych, które reprezentują lokalizacje atomów lub jonów. Cała struktura składa się z komórek powtarzających się w trzech wymiarach, jak pokazano na rysunku 1.

Podane są dwa rysunki. Po lewej stronie przedstawiono sześcian z punktami kratowymi w każdym rogu i komórkami jednostkowymi jako ścianami. Po prawej stronie ten sam sześcian jest powielony szarą czcionką, aby pokazać nieskończoną sieć podobnych sześcianów.

Rysunek 1. Komórka jednostkowa pokazuje lokalizacje punktów kratowych powtarzających się we wszystkich kierunkach.

Zacznijmy nasze badanie struktury sieci krystalicznej i komórek jednostkowych od najprostszej struktury i najbardziej podstawowej komórki jednostkowej. Aby to zobrazować, wyobraźmy sobie, że bierzemy dużą liczbę identycznych kul, takich jak piłki tenisowe, i układamy je równomiernie w pojemniku. Najprostszym sposobem na zrobienie tego byłoby utworzenie warstw, w których kule w jednej warstwie znajdują się bezpośrednio nad kulami w warstwie poniżej, jak pokazano na rysunku 2. Taki układ nazywamy prostą strukturą sześcienną, a komórkę jednostkową prostą komórką sześcienną lub prymitywną komórką sześcienną.

Trzy rysunki tego samego sześcianu z 10.44. Po lewej stronie narysowane są okręgi wokół punktów kratowych. W środku, te okręgi punktów kratowych stają się brązowymi kulami nałożonymi na pudełko. Po prawej stronie widzimy taki sam rendering nieskończonych pudełek jak w 10.44.

Rysunek 2. Gdy atomy metalu ułożone są tak, że kule w jednej warstwie znajdują się bezpośrednio nad lub pod kulami w innej warstwie, struktura sieciowa nazywana jest prostą sześcienną. Zauważ, że kule są w kontakcie.

W prostej strukturze sześciennej, kule nie są upakowane tak ściśle, jak mogłyby być, i „wypełniają” tylko około 52% objętości pojemnika. Jest to stosunkowo nieefektywny układ i tylko jeden metal (polon, Po) krystalizuje się w prostej strukturze sześciennej. Jak pokazano na rysunku 3, ciało stałe o takim układzie składa się z płaszczyzn (lub warstw), w których każdy atom styka się tylko z czterema najbliższymi sąsiadami w swojej warstwie, z atomem znajdującym się bezpośrednio nad nim w warstwie powyżej i z atomem znajdującym się bezpośrednio pod nim w warstwie poniżej. Liczba innych cząsteczek, z którymi styka się każda cząsteczka w krystalicznym ciele stałym jest znana jako jej liczba koordynacyjna. Dla atomu polonu w prostym układzie sześciennym, liczba koordynacyjna wynosi zatem sześć.

Pokazane są dwa rysunki. Po lewej stronie, nieskończony stos sześcianów z 10.44 pojawia się, tym razem tylko w czerni i bieli. Silny nacisk położony jest na jeden punkt kratowy i linie bezpośrednio do niego przylegające na krawędziach sześcianu. Po prawej stronie pojawia się ten sam rysunek, tym razem z punktem kratowym w kolorze czerwonym i liniami promieniującymi od niego oznaczonymi jako 1-6.

Rysunek 3. Atom w prostej strukturze siatki sześciennej kontaktuje się z sześcioma innymi atomami, ma więc liczbę koordynacyjną sześć.

W prostej siatce sześciennej komórką jednostkową, która powtarza się we wszystkich kierunkach, jest sześcian zdefiniowany przez środki ośmiu atomów, jak pokazano na rysunku 4. Atomy w sąsiednich rogach tej komórki stykają się ze sobą, więc długość krawędzi tej komórki jest równa dwóm promieniom atomowym, czyli jednej średnicy atomowej. Sześcienna komórka jednostkowa zawiera tylko te części atomów, które się w niej znajdują. Ponieważ atom w narożniku prostej sześciennej komórki jednostkowej jest zawarty w sumie w ośmiu komórkach jednostkowych, tylko jedna ósma tego atomu znajduje się w danej komórce jednostkowej. A ponieważ każda prosta sześcienna komórka jednostkowa ma jeden atom w każdym z ośmiu „rogów”, jest 8 \times \frac{1}{8}=1 atom wewnątrz jednej prostej sześciennej komórki jednostkowej.

Pokazane są dwa rysunki. Po lewej stronie, pojawia się jednostka sześcienna z 10.45, z kulistymi szarymi cząsteczkami nałożonymi na każdy punkt kratowy, oznaczona jako "prosta sześcienna komórka kratowa". Po prawej stronie, oznaczona jako "8 narożników", znajduje się ta sama jednostka sześcienna, pokazująca tylko fragmenty sfer molekuł, które pojawiłyby się wewnątrz tej jednostki sześciennej.

Rysunek 4. Prosta sześcienna komórka jednostkowa siatki zawiera jedną ósmą atomu w każdym z ośmiu narożników, więc zawiera jeden atom ogółem.

Przykład 1: Obliczanie promienia atomowego i gęstości dla metali, część 1

Długość krawędzi komórki jednostkowej polonu alfa wynosi 336 pm.

  1. Określ promień atomu polonu.
  2. Określ gęstość polonu alfa.
Pokaż rozwiązanie

Polon alfa krystalizuje w prostej sześciennej komórce jednostkowej:

Schemat przedstawia sześcian z jedną ósmą porcją ośmiu kul wewnątrz sześcianu, po jednej sekcji w każdym rogu. Wzdłuż prawej dolnej części sześcianu znajdują się dwie podwójnie zakończone strzałki, z których każda rozciąga się wzdłuż połowy całkowitej odległości w poprzek sześcianu. Każda strzałka jest oznaczona
  1. Dwa sąsiednie atomy Po stykają się ze sobą, więc długość krawędzi tej komórki jest równa dwóm promieniom atomów Po: l=2r. Wobec tego promień Po wynosi r= l=2r.
  2. Gęstość dana jest wzorem \tekst{gęstość}= l= l=2r. Gęstość polonu można znaleźć poprzez określenie gęstości jego komórki jednostkowej (masa zawarta w komórce jednostkowej podzielona przez objętość komórki jednostkowej). Ponieważ komórka jednostkowa Po zawiera jedną ósmą atomu Po w każdym ze swoich ośmiu rogów, komórka jednostkowa zawiera jeden atom Po.

Masę komórki jednostkowej Po można znaleźć przez:

\times \dfrac{tekst{1 atom Po}}{\tekst{1 komórka jednostkowa Po}} \times \dfrac{tekst{1 mol Po}}{6.022 razy {10}^{23}}} atomy Po}} razy dfrac{208.998} g}}{1 mol Po}}=3.47 razy {10}^{-22} tekst{g}

Objętość komórki jednostkowej Po może być znaleziona przez:

V={l}^{3}={(336 razy {10}^{-10} tekst{cm})}^{3}=3.79} razy {10}^{-23}{text{cm}}^{3}

(Zauważ, że długość krawędzi została przeliczona z pm na cm, aby uzyskać zwykłe jednostki objętości dla gęstości.)

Więc, gęstość \tekst{Po}==dfrac{3.471 razy {10}^{-22}}{3,79 razy {10}^{-23}{}}^{3}}={{9,16 g/cm}}^{3}

Check Your Learning

Długość krawędzi komórki jednostkowej dla niklu wynosi 0,3524 nm. Gęstość Ni wynosi 8,90 g/cm3. Czy nikiel krystalizuje się w prostej strukturze sześciennej? Wyjaśnij.

Pokaż rozwiązanie

Nie. Gdyby Ni był prostym sześcianem, jego gęstość byłaby dana przez:

times dfrac{tekst{1 mol Ni}}{6.022 razy {10}^{23}}}{1 mol Ni}}=9,746 razy {10}^{-23}}{1 mol Ni}
V={l}^{3}={(3,524 razy {10}^{-8}}{cm})}^{3}=4.376 razy {10}^{-23}{ tekst{cm}}^{3}

Wtedy gęstość Ni wynosiłaby = =dfrac{9,746 razy {10}^{-23}}}g}}{4,376 razy {10}^{-23}{ tekst{cm}}^{3}}={ tekst{2.23 g/cm}}^{3}

Ponieważ rzeczywista gęstość Ni nie jest do niej zbliżona, Ni nie tworzy prostej struktury sześciennej.

Większość kryształów metali to jeden z czterech głównych typów komórek jednostkowych. Na razie skupimy się na trzech sześciennych komórkach jednostkowych: prostej sześciennej (którą już widzieliśmy), sześciennej skupionej w ciele i sześciennej skupionej w twarzy – wszystkie są zilustrowane na rysunku 5. (Zauważ, że w rzeczywistości istnieje siedem różnych systemów sieciowych, niektóre z nich mają więcej niż jeden typ sieci, w sumie 14 różnych typów komórek jednostkowych. Bardziej skomplikowane geometrie zostawiamy na później w tym module.)

Pierwszy rząd rysunków jest oznaczony jako "lokalizacje punktów kratowych". Pod nim znajdują się trzy obrazy. Po lewej stronie jest prosty sześcian jednostkowy z 6 punktami kratowymi. W środku jest nieco większy sześcian jednostkowy z czerwoną kropką w środku. Po prawej stronie jest jeszcze większy sześcian z 6 czerwonymi kropkami w środku, ułożonymi w dwóch ukośnych rzędach po 3. Dolny rząd rysunków jest oznaczony jako "Komórki sześcianu". Po lewej stronie znajduje się prosta jednostka sześcienna z nałożonymi szarymi molekułami. W środku znajduje się ten sam rysunek, z czerwoną cząsteczką umieszczoną w środku pudełka. Po prawej stronie jest ten sam rysunek, z sześcioma czerwonymi molekułami w dwóch ukośnych liniach wewnątrz pudełka.

Rysunek 5. Sześcienne komórki jednostkowe metali pokazują (na górnych rysunkach) lokalizacje punktów kratowych i (na dolnych rysunkach) atomy metalu znajdujące się w komórce jednostkowej.

Niektóre metale krystalizują w układzie, który ma sześcienną komórkę jednostkową z atomami na wszystkich rogach i atomem w centrum, jak pokazano na rysunku 6. To się nazywa ciało-centered cubic (BCC) stałe. Atomy w narożach komórki BCC nie stykają się ze sobą, ale stykają się z atomem w centrum. Komórka BCC zawiera dwa atomy: jedną ósmą atomu w każdym z ośmiu narożników (8 razy ∗frac{1}{8}=1 atom z narożników) plus jeden atom ze środka. Każdy atom w tej strukturze dotyka czterech atomów w warstwie nad nim i czterech atomów w warstwie pod nim. Zatem atom w strukturze BCC ma liczbę koordynacyjną równą osiem.

Pojawiają się trzy rysunki. Po lewej stronie jest ten sam rysunek jednostki sześciennej z jedną czerwoną kropką w środku, z rysunku 10.48. W środku jest ten sam sześcian z nałożonymi szarymi molekułami, z jedną czerwoną molekułą w środku, jak w dolnym rzędzie rysunku 10.48. Po lewej stronie widzimy, że części molekuł poza sześcianem zostały ogołocone, a pozostały tylko fragmenty szarych molekuł i cała czerwona molekuła.

Rysunek 6. W strukturze sześciennej skupionej w ciele atomy w danej warstwie nie stykają się ze sobą. Każdy atom dotyka czterech atomów w warstwie nad nim i czterech atomów w warstwie pod nim.

Atomy w układach BCC są znacznie efektywniej upakowane niż w prostej strukturze sześciennej, zajmując około 68% całkowitej objętości. Izomorficzne metale o strukturze BCC obejmują K, Ba, Cr, Mo, W, i Fe w temperaturze pokojowej. (Elementy lub związki, które krystalizują się z tej samej struktury mówi się, że są izomorficzne.)

Wiele innych metali, takich jak aluminium, miedź i ołów, krystalizuje się w układzie, który ma sześcienną komórkę jednostkową z atomami na wszystkich rogach i w centrach każdej twarzy, jak pokazano na rysunku 7. Taki układ nazywany jest ciałem stałym FCC (ang. face-centered cubic). Komórka FCC zawiera cztery atomy: jedną ósmą atomu na każdym z ośmiu rogów (8 razy ∗1}{8}=1 atom z rogów) i połowę atomu na każdej z sześciu ścian (6 razy ∗1}{2}=3 atomy z ścian). Atomy w narożach dotykają atomów w środkach sąsiednich ścian wzdłuż przekątnych ścian sześcianu. Ponieważ atomy znajdują się na identycznych punktach kratowych, mają identyczne otoczenia.

Pojawiają się trzy rysunki. Po lewej stronie jest ten sam sześcian z 6 czerwonymi kropkami w środku, jak na rysunku 10.48. W środku znajduje się ta sama jednostka sześcienna z nałożonymi kulistymi cząsteczkami, jak w dolnym rzędzie rysunku 10.48. Po prawej stronie szare molekuły, które znajdują się na zewnątrz sześcianu są ogołocone, pozostawiając tylko fragmenty szarych molekuł i sześć połówek czerwonych molekuł (ponieważ zostały one podzielone na pół).

Rysunek 7. Ciało stałe sześcienne skupione w ścianach ma atomy w narożach i, jak sama nazwa wskazuje, w środkach ścian jego komórek jednostkowych.

Atomy w układzie FCC są upakowane tak blisko siebie, jak to tylko możliwe, przy czym atomy zajmują 74% objętości. Struktura ta jest również nazywana najbliższym upakowaniem sześciennym (CCP). W CCP, istnieją trzy powtarzające się warstwy heksagonalnie ułożonych atomów. Każdy atom styka się z sześcioma atomami w swojej warstwie, trzema w warstwie powyżej i trzema w warstwie poniżej. W tym układzie każdy atom styka się z 12 bliskimi sąsiadami, a więc ma liczbę koordynacyjną 12. Fakt, że układy FCC i CCP są równoważne może nie być od razu oczywisty, ale dlaczego są one właściwie tą samą strukturą jest zilustrowany na rysunku 8.

Pokazane są trzy obrazy. W pierwszym obrazie, widok z boku pokazuje warstwę niebieskich kul, oznaczonych

Rysunek 8. Układ CCP składa się z trzech powtarzających się warstw (ABCABC…) heksagonalnie ułożonych atomów. Atomy w strukturze CCP mają liczbę koordynacyjną 12, ponieważ kontaktują się z sześcioma atomami w swojej warstwie oraz z trzema atomami w warstwie powyżej i trzema atomami w warstwie poniżej. Obracając perspektywę, możemy zobaczyć, że struktura CCP ma komórkę jednostkową z licem zawierającym atom z warstwy A w jednym rogu, atomy z warstwy B po przekątnej (w dwóch rogach i w środku lica) oraz atom z warstwy C w pozostałym rogu. To jest to samo co układ sześcienny face-centered.

Ponieważ bliższe upakowanie maksymalizuje całkowite przyciąganie między atomami i minimalizuje całkowitą energię międzycząsteczkową, atomy w większości metali pakują się w ten sposób. Znajdujemy dwa rodzaje najbliższego upakowania w prostych metalicznych strukturach krystalicznych: CCP, z którym już się spotkaliśmy, oraz heksagonalne najbliższe upakowanie (HCP) pokazane na rysunku 9. Oba składają się z powtarzających się warstw atomów ułożonych heksagonalnie. W obu typach druga warstwa (B) jest umieszczona na pierwszej warstwie (A) w taki sposób, że każdy atom w drugiej warstwie styka się z trzema atomami w pierwszej warstwie. Trzecia warstwa jest umieszczona na jeden z dwóch sposobów. W HCP, atomy w trzeciej warstwie znajdują się bezpośrednio nad atomami w pierwszej warstwie (tj. trzecia warstwa jest również typu A), a stos składa się z naprzemiennych warstw ściśle upakowanych typu A i typu B (tj. ABABAB⋯). W CCP atomy w trzeciej warstwie nie znajdują się powyżej atomów w żadnej z dwóch pierwszych warstw (tj. trzecia warstwa jest typu C), a stos składa się z naprzemiennie ułożonych warstw typu A, typu B i typu C (tj. ABCABCABC⋯). Około dwie trzecie wszystkich metali krystalizuje się w układach najbliżej upakowanych o liczbach koordynacyjnych 12. Metale, które krystalizują się w strukturze HCP obejmują Cd, Co, Li, Mg, Na i Zn, a metale, które krystalizują się w strukturze CCP obejmują Ag, Al, Ca, Cu, Ni, Pb i Pt.

Pokazano dwa obrazy. Pierwszy obraz, oznaczony

Rysunek 9. W obu typach najbliższego upakowania, atomy są upakowane tak zwarcie jak to tylko możliwe. Heksagonalne najbliższe upakowanie składa się z dwóch naprzemiennych warstw (ABABABAB…). Najbliższe upakowanie sześcienne składa się z trzech naprzemiennych warstw (ABCABCABC…).

Przykład 2: Obliczanie promienia atomowego i gęstości dla metali, część 2

Wapń krystalizuje się w strukturze sześciennej. Długość krawędzi jego komórki jednostkowej wynosi 558.8 pm.

  1. Jaki jest promień atomowy Ca w tej strukturze?
  2. Oblicz gęstość Ca.
Pokaż rozwiązanie

Część 1

Przedstawione są dwa rysunki. Na prawym, "heksagonalnym najbliżej upakowanym", widzimy widok z boku 4 rzędów kul. Górna i trzecia warstwa są zielone, a 2. i 4. warstwa są niebieskie. Po prawej stronie, "cubic closest packed", widzimy widok z boku czterech rzędów kul. Górny i dolny rząd są niebieskie (górny jest oznaczony jako warstwa C). Drugi rząd jest zielony, i oznaczony jako warstwa B. Trzeci rząd jest fioletowy, i oznaczony jako warstwa A.

W strukturze FCC, atomy Ca kontaktują się ze sobą w poprzek przekątnej twarzy, więc długość przekątnej jest równa czterem promieniom atomowym Ca (d = 4r). Dwie sąsiednie krawędzie i przekątna lica tworzą trójkąt prosty, o długości każdego boku równej 558,8 pm i długości przeciwprostokątnej równej czterem promieniom atomowym Ca:

{tekstekst}}^{2}+{tekst}^{2}={tekst}d}^{2}}longrightarrow {(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}={(4r)}^{2}

Solving this gives r=\sqrt{\dfrac{{(558.8\text{pm})}^{2}+{(558.5\\pm})}^{2}}{16}}=}text{197.6 pmg dla promienia Ca}.

Część 2

Gęstość jest dana wzorem \text{density}= \dfrac{\text{mass}}{\text{volume}}. Gęstość wapnia można znaleźć poprzez określenie gęstości jego komórki jednostkowej: na przykład, masa zawarta w komórce jednostkowej podzielona przez objętość komórki jednostkowej. Komórka Ca ma jedną ósmą atomu na każdym z ośmiu rogów (8 razy \dfrac{1}{8}=1\text{atom}}prawej) i jedną połowę atomu na każdej z sześciu ścian (6 razy \dfrac{1}{2}=3\text{atom}}prawej), w sumie cztery atomy w komórce.

Masa komórki jednostkowej może być znaleziona przez:

\\times \dfrac{4 atomy Ca}}{\times \times \times \times {1 mol Ca}}{6.022 razy {10}^{23}}} atomy Ca}} razy dfrac{40.078}g}}{1 mol Ca}}=2.662 razy {10}^{-22}} tekst{g}

Objętość komórki jednostkowej Ca może być znaleziona przez:

V={a}^{3}={(558.8 razy {10}^{-10} tekst{cm})}^{3}=1.745 razy {10}^{-22}{\text{cm}}^{3}

(Zauważ, że długość krawędzi została przeliczona z pm na cm, aby uzyskać zwykłe jednostki objętości dla gęstości.)

Wtedy gęstość \\\Ca}= \dfrac{2.662 razy {10}^{-22}}g}}{1.745 razy {10}^{-22}{\C}^{3}}={\}text{1.53 g/cm}}^{3}

Check Your Learning

Srebro krystalizuje w strukturze FCC. Długość krawędzi jego komórki jednostkowej wynosi 409 pm.

  1. Jaki jest promień atomowy Ag w tej strukturze?
  2. Oblicz gęstość Ag.
Pokaż rozwiązania

  1. 144 pm
  2. 10.5 g/cm3

W ogólności komórka jednostkowa jest zdefiniowana przez długości trzech osi (a, b, i c) i kąty (α, β, i γ) między nimi, jak pokazano na rysunku 10. Osie są zdefiniowane jako długości pomiędzy punktami w siatce przestrzennej. W związku z tym osie komórek jednostkowych łączą punkty o identycznych otoczeniach.

Przedstawiono rysunek jednostki sześciennej z punktami kratowymi. Płaszczyzny powierzchni sześcianu są oznaczone a, b, i c. Wokół jednego punktu kratowego pojawia się krąg strzałek oznaczonych (α, β, i γ).

Rysunek 10. Komórka jednostkowa jest zdefiniowana przez długości jej trzech osi (a, b, i c) oraz kąty (α, β, i γ) między tymi osiami.

Istnieje siedem różnych systemów kratowych, niektóre z nich mają więcej niż jeden typ kraty, w sumie czternaście różnych komórek jednostkowych, które mają kształty pokazane na rysunku 11.

Tabela składająca się z 7 wierszy, z dwiema kolumnami zatytułowanymi System/Aksyle/Kąty i Komórki jednostkowe.

Rysunek 11. Istnieje siedem różnych układów sieciowych i 14 różnych komórek jednostkowych.

Struktury kryształów jonowych

Kryształy jonowe składają się z dwóch lub więcej różnych rodzajów jonów, które zwykle mają różne rozmiary. Upakowanie tych jonów w strukturę kryształu jest bardziej złożone niż upakowanie atomów metalu o tym samym rozmiarze.

Większość jonów jednoatomowych zachowuje się jak naładowane kule, a ich przyciąganie do jonów o przeciwnym ładunku jest takie samo w każdym kierunku. W konsekwencji, stabilne struktury związków jonowych powstają (1) gdy jony o jednym ładunku są otoczone przez jak najwięcej jonów o przeciwnym ładunku i (2) gdy kationy i aniony są w kontakcie ze sobą. Struktury są określane przez dwa główne czynniki: względne rozmiary jonów i stosunek liczby jonów dodatnich i ujemnych w compound.

Obraz przedstawia widok z góry na warstwę niebieskich kul ułożonych w arkuszu leżącym na innym arkuszu, który jest taki sam, z wyjątkiem kul są zielone. Drugi arkusz jest przesunięty tylko trochę tak, że kule z górnego arkusza leżą w rowkach drugiego arkusza. Trzeci arkusz składający się z fioletowych kul leży na dole. Przestrzenie utworzone pomiędzy sferami w każdej warstwie są oznaczone

Rys. 12. Kationy mogą zajmować dwa rodzaje otworów pomiędzy anionami: otwory oktaedryczne lub otwory tetraedryczne.

W prostych strukturach jonowych znajdujemy zwykle aniony, które są zwykle większe od kationów, ułożone w szyku najbliżej siebie. (Jak widać wcześniej, dodatkowe elektrony przyciągane do tego samego jądra powodują, że aniony są większe, a mniej elektronów przyciąganych do tego samego jądra powoduje, że kationy są mniejsze w porównaniu z atomami, z których są utworzone). Mniejsze kationy zwykle zajmują jeden z dwóch rodzajów dziur (lub szczelin) pozostałych pomiędzy anionami. Mniejszy z otworów znajduje się pomiędzy trzema anionami w jednej płaszczyźnie i jednym anionem w płaszczyźnie sąsiedniej. Cztery aniony otaczające ten otwór są rozmieszczone w narożach czworościanu foremnego, dlatego otwór ten nazywamy otworem czworościanowym. Większy typ dziury znajduje się w centrum sześciu anionów (trzy w jednej warstwie i trzy w sąsiedniej) rozmieszczonych na rogach ośmiościanu; nazywamy go dziurą oktaedryczną. Rysunek 12 ilustruje oba te typy otworów.

Zależnie od względnych rozmiarów kationów i anionów, kationy związku jonowego mogą zajmować otwory tetraedryczne lub oktaedryczne, jak pokazano na rysunku 13. Stosunkowo małe kationy zajmują otwory tetraedryczne, a większe kationy zajmują otwory oktaedryczne. Jeśli kationy są zbyt duże, aby zmieścić się w otworach oktaedrycznych, aniony mogą przyjąć bardziej otwartą strukturę, taką jak prosty układ sześcienny. Większe kationy mogą wtedy zajmować większe otwory sześcienne możliwe przez bardziej otwarty spacing.

Trzy rysunki kostek kratowych są podane. Po lewej stronie, dolna lewa jednostka sześcienna ma zielone punkty kratowe, a wszystkie inne sześciany mają fioletowe (oznaczone jako Tetrahedral otwór). W środku punkty kratowe są albo zielone, albo pomarańczowe, na linii ukośnej (oznaczenie otworu oktaedrycznego). Po prawej stronie, wszystkie punkty kratowe są fioletowe, oznaczone jako Cubic hole.

Rysunek 13. Wielkość kationu i kształt otworu zajmowanego przez związek są ze sobą bezpośrednio związane.

W układzie HCP lub CCP anionów na każdy anion przypadają dwa otwory tetraedryczne. Związek, który krystalizuje się w najbliżej upakowanym układzie anionów z kationami w otworach tetraedrycznych może mieć maksymalny stosunek kationu do anionu 2:1; wszystkie otwory tetraedryczne są wypełnione w tym stosunku. Przykłady obejmują Li2O, Na2O, Li2S i Na2S. Związki o stosunku mniejszym niż 2:1 mogą również krystalizować się w najbliżej upakowanym układzie anionów z kationami w otworach tetraedrycznych, jeśli rozmiary jonów pasują. W tych związkach, jednakże, niektóre z otworów tetraedrycznych pozostają wolne.

Przykład 3: Zajmowanie otworów tetraedrycznych

Siarczek cynku jest ważnym przemysłowym źródłem cynku i jest również używany jako biały pigment w farbie. Siarczek cynku krystalizuje się z jonami cynku zajmującymi połowę otworów tetraedrycznych w najbliżej upakowanym układzie jonów siarczkowych. Jaki jest wzór siarczku cynku?

Pokaż rozwiązanie

Ponieważ na jeden anion (jon siarczkowy) przypadają dwa otwory tetraedryczne, a połowa tych otworów jest zajęta przez jony cynku, na jeden jon siarczkowy musi przypadać ∗1}{2} razy 2, czyli 1 jon cynku. Zatem, wzór to ZnS.

Check Your Learning

Selenek litu może być opisany jako najbliżej upakowany układ jonów selenkowych z jonami litu we wszystkich otworach tetraedrycznych. Jaki jest wzór selenku litu?

Pokaż rozwiązanie

Li2Se

Stosunek dziur oktaedrycznych do anionów w strukturze HCP lub CCP wynosi 1:1. Tak więc związki z kationami w otworach oktaedrycznych w najbliżej upakowanym układzie anionów mogą mieć maksymalny stosunek kationu do anionu 1:1. W NiO, MnS, NaCl i KH, na przykład, wszystkie otwory oktaedryczne są wypełnione. Stosunek mniejszy niż 1:1 jest obserwowany, gdy niektóre z otworów oktaedrycznych pozostają puste.

Przykład 4: Stechiometria związków jonowych

Szafir jest tlenkiem glinu. Tlenek glinu krystalizuje się z jonami glinu w dwóch trzecich oktaedrycznych otworów w najbliższym upakowanym układzie jonów tlenku. Jaki jest wzór tlenku glinu?

Pokaż rozwiązanie

Ponieważ na każdy anion (jon tlenku) przypada jeden otwór oktaedryczny i tylko dwie trzecie tych otworów jest zajętych, stosunek glinu do tlenu musi wynosić \frac{2}{3} :1, co dałoby {{text{Al}}_{2}text{/}3}}O}. Najprostszy stosunek liczb całkowitych to 2:3, więc wzór to Al2O3.

Check Your Learning

Biały pigment tlenek tytanu krystalizuje z jonami tytanu w jednej połowie oktaedrycznych otworów w najbliżej upakowanym układzie jonów tlenku. Jaki jest wzór tlenku tytanu?

Pokaż rozwiązanie

TiO2

W prostym sześciennym układzie anionów istnieje jeden sześcienny otwór, który może być zajęty przez kation dla każdego anionu w układzie. W CsCl, a także w innych związkach o tej samej strukturze, wszystkie otwory sześcienne są zajęte. Połowa dziur sześciennych jest zajęta w SrH2, UO2, SrCl2 i CaF2.

Różne typy związków jonowych często krystalizują się w tej samej strukturze, gdy względne rozmiary ich jonów i ich stechiometria (dwie główne cechy określające strukturę) są podobne.

Komórki związków jonowych

Wiele związków jonowych krystalizuje z sześciennymi komórkami jednostkowymi, i będziemy używać tych związków do opisania ogólnych cech struktur jonowych.

Gdy związek jonowy składa się z kationów i anionów o podobnych rozmiarach w stosunku 1:1, zazwyczaj tworzy prostą strukturę sześcienną. Chlorek cezu, CsCl, (pokazany na rysunku 14) jest tego przykładem, gdzie Cs+ i Cl- mają promienie odpowiednio 174 pm i 181 pm. Możemy o tym myśleć jako o jonach chlorkowych tworzących prostą sześcienną komórkę jednostkową, z jonem cezu w środku; lub jako o jonach cezu tworzących komórkę jednostkową z jonem chlorkowym w środku; lub jako o prostych sześciennych komórkach jednostkowych utworzonych przez jony Cs+ nakładających się na komórki jednostkowe utworzone przez jony Cl-. Jony cezu i jony chlorkowe stykają się wzdłuż przekątnych ciała komórek jednostkowych. Jeden jon cezu i jeden jon chlorkowy są obecne w każdej komórce jednostkowej, co daje stechiometrię l:l wymaganą przez wzór na chlorek cezu. Zauważ, że nie ma punktu kratowego w centrum komórki, a CsCl nie jest strukturą BCC, ponieważ jon cezu nie jest identyczny z jonem chlorku.

Trzy rysunki są pokazane. Po lewej stronie jest nieskończony sześcienny jednostkowy rendering, z dolnym lewym sześcianie zawierającym jedną czerwoną kropkę w jego centrum. W środku, ten jeden sześcian pojawia się, z punktami kratowymi jako duże fioletowe kule. Centralna molekuła jest mniejsza i ma kolor zielony. Po prawej stronie pojawia się stos sześcianów z fioletowymi kulami, a pomiędzy nimi małe zielone kule pokazane z jednej strony.

Rysunek 14. Związki jonowe o podobnych rozmiarach kationów i anionów, takie jak CsCl, tworzą zwykle prostą strukturę sześcienną. Można je opisać komórkami jednostkowymi z kationami w narożach lub anionami w narożach.

Powiedzieliśmy, że położenie punktów sieci jest dowolne. Ilustruje to alternatywny opis struktury CsCl, w którym punkty kratowe znajdują się w centrach jonów cezu. W tym opisie, jony cezu znajdują się na punktach kratowych w rogach komórki, a jon chlorkowy w centrum komórki. Te dwie komórki jednostkowe są różne, ale opisują identyczne struktury.

Gdy związek jonowy składa się z kationów i anionów w stosunku 1:1, które różnią się znacznie pod względem wielkości, zazwyczaj krystalizuje z komórką jednostkową FCC, jak pokazano na rysunku 15. Chlorek sodu, NaCl, jest tego przykładem, gdzie Na+ i Cl- mają promienie odpowiednio 102 pm i 181 pm. Możemy myśleć o tym, że jony chlorkowe tworzą komórkę FCC, z jonami sodu umieszczonymi w otworach oktaedrycznych w środku krawędzi komórki i w jej centrum. Jony sodu i chlorkowe stykają się wzdłuż krawędzi komórki. Komórka jednostkowa zawiera cztery jony sodu i cztery jony chlorkowe, dając stechiometrię 1:1 wymaganą przez wzór, NaCl.

Trzy obrazy są pokazane. Pierwszy obraz pokazuje sześcian z czarnymi kropkami w każdym rogu i czerwoną kropką w centrum. Ten sześcian jest ułożone z siedmiu innych, które nie są kolorowe, aby utworzyć większy sześcian. Drugi obraz składa się z ośmiu sfer, które są zgrupowane razem, aby utworzyć sześcian z jednym znacznie większa kula w centrum. Nazwa pod tym obrazem brzmi

Figura 15. Związki jonowe, w których aniony są znacznie większe od kationów, takie jak NaCl, tworzą zwykle strukturę FCC. Mogą one być opisane przez komórki jednostkowe FCC z kationami w otworach oktaedrycznych.

Kubiczna forma siarczku cynku, blenda cynkowa, również krystalizuje w komórce jednostkowej FCC, jak pokazano na rysunku 16. Struktura ta zawiera jony siarczkowe w punktach siatki FCC. (Ułożenie jonów siarczkowych jest identyczne jak ułożenie jonów chlorkowych w chlorku sodu). Promień jonu cynku wynosi tylko około 40% promienia jonu siarczku, więc te małe jony Zn2+ znajdują się w naprzemiennych otworach tetraedrycznych, czyli w jednej połowie otworów tetraedrycznych. W komórce jednostkowej znajdują się cztery jony cynku i cztery jony siarczkowe, co daje wzór empiryczny ZnS.

Pojawiają się dwa rysunki. Po lewej stronie, nieskończona struktura sześcienna jest renderowana, z lewym dolnym sześcianem zawierającym sześć czerwonych kropek. Po prawej stronie, ten jeden sześcian jest powiększony, a żółte kropki pojawiają się w losowych odstępach na krawędziach i wewnątrz sześcianu, aby reprezentować punkty kratowe.

Rysunek 16. ZnS, siarczek cynku (lub blenda cynkowa) tworzy komórkę jednostkową FCC z jonami siarczku w punktach kratowych i znacznie mniejszymi jonami cynku zajmującymi połowę otworów tetraedrycznych w strukturze.

Komórka jednostkowa fluorku wapnia, jak ta pokazana na rysunku 17, jest również komórką jednostkową FCC, ale w tym przypadku kationy znajdują się na punktach kratowych; równoważne jony wapnia znajdują się na punktach kratowych sieci FCC. Wszystkie miejsca tetraedryczne w układzie FCC jonów wapnia są zajęte przez jony fluorkowe. W komórce jednostkowej znajdują się cztery jony wapnia i osiem jonów fluoru, co daje stosunek wapnia do fluoru wynoszący l:2, zgodnie ze wzorem chemicznym CaF2. Dokładna analiza rysunku 17 ujawni prosty układ sześcienny jonów fluorkowych z jonami wapnia w jednej połowie otworów sześciennych. Struktura ta nie może być opisana w kategoriach przestrzennej siatki punktów na jonach fluorkowych, ponieważ nie wszystkie jony fluorkowe mają identyczne otoczenie. Orientacja czterech jonów wapnia względem jonów fluorkowych jest różna.

Pojawiają się dwa rysunki. Po lewej stronie jest nieskończona struktura sześcienna renderowania, z dolnej lewej kostki zawierającej sześć czerwonych kropek. Po prawej stronie, ten jeden sześcian jest powiększony, aby pokazać wiele zielonych kul, w rogach sześcianu i we wnętrzu. Wszystkie są połączone liniami. Oznaczona CaF2 twarzo-centryczna komórka jednostkowa.

Rysunek 17. Fluorek wapnia, CaF2, tworzy komórkę jednostkową FCC z jonami wapnia (zielony) w punktach kratowych i jonami fluoru (czerwony) zajmującymi wszystkie miejsca tetraedryczne pomiędzy nimi.

Obliczanie promieni jonowych

Jeśli znamy długość krawędzi komórki jednostkowej związku jonowego i położenie jonów w komórce, możemy obliczyć promienie jonowe dla jonów w związku, jeśli przyjmiemy założenia dotyczące indywidualnych kształtów jonów i kontaktów.

Przykład 5: Obliczanie promieni jonowych

Długość krawędzi komórki jednostkowej LiCl (struktura podobna do NaCl, FCC) wynosi 0.514 nm lub 5,14 Å. Zakładając, że jon litu jest na tyle mały, że jony chlorkowe są w kontakcie, jak na rysunku 15, oblicz promień jonowy dla jonu chlorkowego.

Uwaga: Jednostka długości angstrem, Å, jest często używana do reprezentowania wymiarów w skali atomowej i jest równoważna 10-10 m.

Pokaż rozwiązanie

Na powierzchni czołowej komórki jednostkowej LiCl jony chlorkowe stykają się ze sobą po przekątnej powierzchni czołowej:

Pokazane są trzy obrazy. Pierwszy pokazuje sześcian z naprzemiennie zielonych i fioletowych sfer. Mniejszy sześcian wewnątrz tego sześcianu jest zarysowany, a następnie pojawia się jego większa wersja. Ta figura to szary sześcian, który wydaje się być zbudowany z kul. Pomiędzy każdą sferą są małe odstępy. W tym sześcianie jest zarysowany trójkąt prosty, a jego większa wersja pojawia się obok. Ten trójkąt prosty ma dwa boki oznaczone

Rysując trójkąt prosty na powierzchni komórki jednostkowej, widzimy, że długość przekątnej jest równa czterem promieniom chlorku (jeden promień od każdego narożnego chlorku i jedna średnica – co równa się dwóm promieniom – od jonu chlorku w centrum powierzchni), więc d = 4r. Z twierdzenia pitagorejskiego wynika, że:

{tekst}^{2}+{tekst}^{2}={tekst}^{2}

co daje:

Lewa(0.514 tekst{ nm}} prawa)^{2}+Lewa(0.514\text{ nm}\right)^{2}={\left(4r\right)}^{2}=16{r}^{2}

Solving this gives:

r=\sqrt{\dfrac{{(0.514\text{nm})}^{2}+{(0.514\text{nm})}^{2}}{16}}=\text{0.182 nm} (1,82 Å) dla promienia Cl-

Check Your Learning

Długość krawędzi komórki jednostkowej KCl (struktura podobna do NaCl, FCC) wynosi 6,28 Å. Zakładając kontakt anion-kation wzdłuż krawędzi komórki, oblicz promień jonu potasowego. Promień jonu chlorkowego wynosi 1,82 Å.

Pokaż rozwiązanie

Promień jonu potasowego wynosi 1,33 Å.

Należy zdać sobie sprawę, że wartości promieni jonowych obliczone na podstawie długości krawędzi komórek jednostkowych zależą od wielu założeń, takich jak doskonały kulisty kształt jonów, które w najlepszym przypadku są przybliżeniami. Stąd, tak wyliczone wartości są same w sobie przybliżone i porównania nie mogą być zbyt daleko posunięte. Niemniej jednak metoda ta okazała się przydatna do obliczania promieni jonowych z pomiarów eksperymentalnych, takich jak oznaczenia krystalografii rentgenowskiej.

Krystalografia rentgenowska

Rozmiar komórki jednostkowej i układ atomów w krysztale może być określony na podstawie pomiarów dyfrakcji promieniowania rentgenowskiego przez kryształ, co określa się mianem krystalografii rentgenowskiej. Dyfrakcja to zmiana kierunku przemieszczania się fali elektromagnetycznej, gdy napotyka ona na fizyczną barierę, której wymiary są porównywalne z wymiarami długości fali światła. Promieniowanie rentgenowskie jest promieniowaniem elektromagnetycznym o długości fali mniej więcej tak długiej, jak odległość między sąsiednimi atomami w kryształach (rzędu kilku Å).

Gdy wiązka monochromatycznego promieniowania rentgenowskiego uderza w kryształ, jego promienie są rozpraszane we wszystkich kierunkach przez atomy w krysztale. Kiedy rozproszone fale poruszające się w tym samym kierunku napotykają na siebie, ulegają interferencji, procesowi, w którym fale łączą się, dając albo wzrost, albo spadek amplitudy (intensywności) w zależności od stopnia, w jakim maksima łączących się fal są od siebie oddzielone (patrz rysunek 18).

Prezentowana jest para obrazów, która ma cztery odcinki. W pierwszym odcinku pokazane są dwie fale sinusoidalne, jedna narysowana nad drugą, a odcinek od wierzchołka jednej krzywej do wierzchołka następnej krzywej jest oznaczony

Rysunek 18. Fale świetlne zajmujące tę samą przestrzeń ulegają interferencji, łącząc się w celu uzyskania fal o większym (a) lub mniejszym (b) natężeniu, w zależności od separacji ich maksimów i minimów.

Gdy promienie X o określonej długości fali, λ, są rozpraszane przez atomy w sąsiednich płaszczyznach krystalicznych oddzielonych od siebie odległością, d, mogą ulegać konstruktywnej interferencji, gdy różnica między odległościami przebytymi przez dwie fale przed ich połączeniem jest czynnikiem całkowitym, n, długości fali. Warunek ten jest spełniony, gdy kąt rozproszonej wiązki, θ, jest związany z długością fali i odległością międzyatomową równaniem:

n{lambda }=2d}theta

Zależność ta jest znana jako równanie Bragga na cześć W. H. Bragga, angielskiego fizyka, który jako pierwszy wyjaśnił to zjawisko. Rysunek 19 ilustruje dwa przykłady dyfrakcji fal z tych samych dwóch płaszczyzn kryształu. Rysunek po lewej stronie przedstawia fale rozproszone pod kątem Bragga, co powoduje interferencję konstruktywną, natomiast rysunek po prawej stronie przedstawia dyfrakcję i inny kąt, który nie spełnia warunku Bragga, co powoduje interferencję destruktywną.

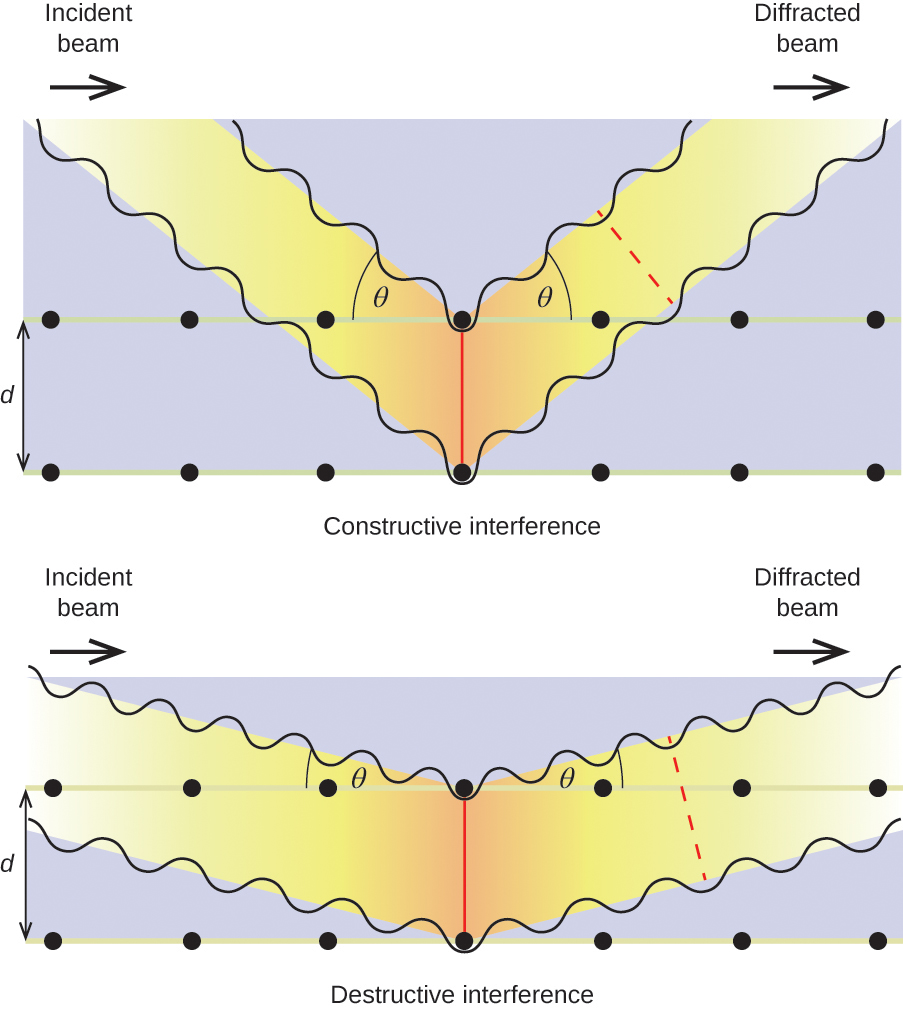
Pokazane są dwa podobne rysunki. Pierwszy rysunek, oznaczony

Rysunek 19. Dyfrakcja promieniowania rentgenowskiego rozproszonego przez atomy w krysztale pozwala na określenie odległości między atomami. Górny obraz przedstawia konstruktywną interferencję pomiędzy dwoma rozproszonymi falami i wynikową falę dyfrakcyjną o dużej intensywności. Dolny obraz przedstawia interferencję destrukcyjną i falę dyfrakcyjną o niskiej intensywności.

Odwiedź „Co to jest prawo Bragga i dlaczego jest ważne?”, aby uzyskać więcej szczegółów na temat równania Bragga i symulatora, który pozwala zbadać wpływ każdej zmiennej na intensywność fali dyfrakcyjnej.

Dyfraktometr rentgenowski, taki jak ten przedstawiony na rysunku 20, może być użyty do pomiaru kątów, pod którymi promienie X ulegają dyfrakcji podczas oddziaływania z kryształem, jak opisano powyżej. Z takich pomiarów równanie Bragga może być wykorzystane do obliczania odległości między atomami, jak zademonstrowano w następującym przykładowym ćwiczeniu.

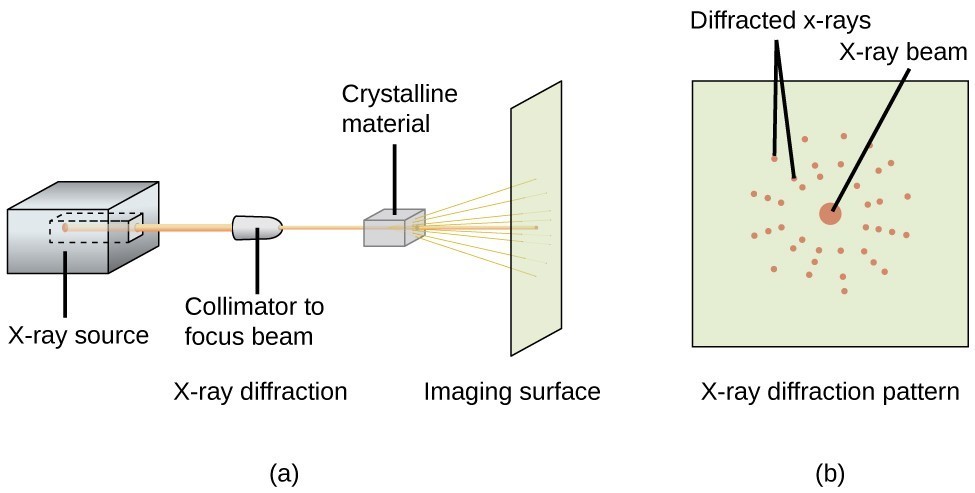
Podano dwa zestawy rysunków. Po prawej stronie, a) jest widok z boku na promieniowanie rentgenowskie rzutowane z maszyny na ścianę, przechodzące przez materiał krystaliczny. Po prawej stronie, b) jest zdjęcie ściany od strony głowy, pokazujące wiązkę promieniowania rentgenowskiego i powstałe w ten sposób dyfrakcje.

Rysunek 20. W dyfraktometrze (a), wiązka promieni X uderza w materiał krystaliczny, dając wzór dyfrakcji promieni X (b), który może być analizowany w celu określenia struktury krystalicznej.

Możesz zobaczyć transkrypcję do „Celebrating Crystallography – An animated adventure” tutaj (otwiera się w nowym oknie).

Przykład 6: Użycie równania Bragga

W dyfraktometrze, promienie X o długości fali 0,1315 nm zostały użyte do wytworzenia wzoru dyfrakcyjnego dla miedzi. Dyfrakcja pierwszego rzędu (n = 1) wystąpiła pod kątem θ = 25,25°. Wyznacz odstępy między płaszczyznami dyfrakcyjnymi w miedzi.

Pokaż rozwiązanie

Odstępy między płaszczyznami znajdujemy rozwiązując równanie Bragga, nλ = 2d sin θ, dla d.

To daje: d=dfrac{nambda}{2 sin θ}= d=dfrac{1 lewa(0.1315}}{2}sin}left(25.25^{circ}}}=0.154}

Check Your Learning

Kryształ o odstępach między płaszczyznami równych 0.394 nm dyfunduje promienie X o długości fali 0.147 nm. Jaki jest kąt dyfrakcji pierwszego rzędu?

Pokaż rozwiązanie

10.8°

Portret chemika: X-ray Crystallographer Rosalind Franklin

Obraz przedstawia okrągłą ilustrację z pierścieniami kropek, które są ze sobą rozmyte.

Rysunek 21. Ilustracja przedstawia obraz dyfrakcji rentgenowskiej podobny do tego, który Franklin znalazła w swoich badaniach. (kredyt: National Institutes of Health)

Odkrycie struktury DNA w 1953 roku przez Francisa Cricka i Jamesa Watsona jest jednym z największych osiągnięć w historii nauki. Otrzymali oni w 1962 roku Nagrodę Nobla w dziedzinie fizjologii lub medycyny, wraz z Maurice Wilkinsem, który dostarczył eksperymentalny dowód struktury DNA. Brytyjska chemiczka Rosalind Franklin wniosła nieoceniony wkład w to monumentalne osiągnięcie dzięki swojej pracy przy pomiarach obrazów dyfrakcji rentgenowskiej DNA. Na początku swojej kariery Franklin prowadziła badania nad strukturą węgli, które okazały się pomocne w brytyjskim wysiłku wojennym. Po przeniesieniu punktu ciężkości na systemy biologiczne na początku lat 50-tych, Franklin wraz z doktorantem Raymondem Goslingiem odkryła, że DNA składa się z dwóch form: długiego, cienkiego włókna tworzącego się, gdy jest mokre (typ „B”) i krótkiego, szerokiego włókna tworzącego się, gdy jest wysuszone (typ „A”). Jej obrazy dyfrakcji rentgenowskiej DNA (rysunek 21) dostarczyły kluczowych informacji, które pozwoliły Watsonowi i Crickowi potwierdzić, że DNA tworzy podwójną helisę, oraz określić szczegóły jego wielkości i struktury.

Franklin prowadziła również pionierskie badania nad wirusami i RNA, które zawiera ich informację genetyczną, odkrywając nowe informacje, które radykalnie zmieniły zasób wiedzy w tej dziedzinie. Po zachorowaniu na raka jajnika Franklin kontynuowała pracę aż do śmierci w 1958 roku w wieku 37 lat. Wśród wielu pośmiertnych uznań jej pracy, Chicago Medical School of Finch University of Health Sciences zmieniła nazwę na Rosalind Franklin University of Medicine and Science w 2004 roku i przyjęła obraz jej słynnego dyfrakcji rentgenowskiej obrazu DNA jako oficjalne logo uniwersytetu.

Key Concepts and Summary

Struktury metali krystalicznych i prostych związków jonowych mogą być opisane w kategoriach pakowania sfer. Atomy metali mogą pakować się w heksagonalne struktury najbliżej upakowane, sześcienne struktury najbliżej upakowane, struktury ze środkiem ciała i proste struktury sześcienne. Aniony w prostych strukturach jonowych powszechnie przyjmują jedną z tych struktur, a kationy zajmują przestrzenie pozostałe pomiędzy anionami. Małe kationy zwykle zajmują otwory tetraedryczne w najbliżej upakowanym układzie anionów. Większe kationy zajmują zwykle otwory oktaedryczne. Jeszcze większe kationy mogą zajmować otwory sześcienne w prostym, sześciennym układzie anionów. Strukturę ciała stałego można opisać poprzez wskazanie wielkości i kształtu komórki jednostkowej oraz zawartości komórki. Rodzaj struktury i wymiary komórki jednostkowej można określić na podstawie pomiarów dyfrakcji promieniowania rentgenowskiego.

Równania kluczowe

  • n{lambda }=2dt

Try It

  1. Opisać strukturę krystaliczną żelaza, które krystalizuje z dwoma równoważnymi atomami metalu w sześciennej komórce jednostkowej.
  2. Opisz strukturę krystaliczną Pt, który krystalizuje się z czterema równoważnymi atomami metalu w sześciennej komórce jednostkowej.
  3. Jaka jest liczba koordynacyjna atomu chromu w strukturze sześciennej skupionej w ciele chromu?
  4. Jaka jest liczba koordynacyjna atomu glinu w strukturze sześciennej skupionej w twarzy glinu?
  5. Metal kobaltowy krystalizuje w strukturze heksagonalnej najbliżej upakowanej. Jaka jest liczba koordynacyjna atomu kobaltu?
  6. Metal nikiel krystalizuje w strukturze sześciennej najbliżej upakowanej. Jaka jest liczba koordynacyjna atomu niklu?
  7. Wolfram krystalizuje w sześciennej komórce jednostkowej o długości krawędzi 3,165 Å.
    1. Jaki jest promień atomowy wolframu w tej strukturze?
    2. Oblicz gęstość wolframu.
  8. Platyn (promień atomowy = 1,38 Å) krystalizuje w sześciennej strukturze ściśle upakowanej. Oblicz długość krawędzi komórki jednostkowej face-centered cubic i gęstość platyny.
  9. Barium krystalizuje w ciele-centered cubic komórki jednostkowej o długości krawędzi 5.025 Å
    1. Jaki jest promień atomowy baru w tej strukturze?
    2. Oblicz gęstość baru.
  10. Aluminium (promień atomowy = 1,43 Å) krystalizuje w sześciennej ściśle upakowanej struktury. Oblicz długość krawędzi komórki jednostkowej face-centered cubic i gęstości aluminium.
  11. Gęstość aluminium jest 2,7 g/cm3; że z krzemu jest 2,3 g/cm3. Wyjaśnij, dlaczego Si ma mniejszą gęstość, mimo że ma cięższe atomy.
  12. Wolna przestrzeń w metalu może być znaleziony przez odjęcie objętości atomów w komórce jednostkowej z objętości komórki. Oblicz procent wolnej przestrzeni w każdej z trzech siatek sześciennych, jeśli wszystkie atomy w każdej z nich są jednakowej wielkości i dotykają swoich najbliższych sąsiadów. Która z tych struktur reprezentuje najbardziej efektywne upakowanie? To znaczy, który pakuje z najmniejszą ilością niewykorzystanej przestrzeni?
  13. Siarczek kadmu, czasami używany jako żółty pigment przez artystów, krystalizuje się z kadmem, zajmując połowę tetraedrycznych otworów w najbliższym upakowanym układzie jonów siarczkowych. Jaki jest wzór siarczku kadmu? Wyjaśnij swoją odpowiedź.
  14. Związek kadmu, cyny i fosforu jest używany w produkcji niektórych półprzewodników. Krystalizuje z kadmu zajmując jedną czwartą tetraedrycznych otworów i cyny zajmując jedną czwartą tetraedrycznych otworów w najbliższym upakowany układ jonów fosforkowych. Jaki jest wzór tego związku? Wyjaśnij swoją odpowiedź.
  15. Jaki jest wzór magnetycznego tlenku kobaltu, stosowanego w taśmach do nagrywania, który krystalizuje się z atomami kobaltu zajmującymi jedną ósmą otworów tetraedrycznych i jedną połowę otworów oktaedrycznych w ściśle upakowanym układzie jonów tlenkowych?
  16. Związek zawierający cynk, glin i siarkę krystalizuje się z najbliżej upakowanym układem jonów siarczkowych. Jony cynku znajdują się w jednej ósmej otworów tetraedrycznych, a jony glinu w jednej połowie otworów oktaedrycznych. Jaki jest wzór empiryczny tego związku?
  17. Związek talu i jodu krystalizuje w prostym układzie sześciennym jonów jodkowych z jonami talu we wszystkich otworach sześciennych. Jaki jest wzór tego jodku? Wyjaśnij swoją odpowiedź.
  18. Który z poniższych pierwiastków reaguje z siarką tworząc ciało stałe, w którym atomy siarki tworzą najbliżej upakowany układ z zajętymi wszystkimi otworami oktaedrycznymi: Li, Na, Be, Ca lub Al?
  19. Jaki jest procent masowy tytanu w rutylu, minerale zawierającym tytan i tlen, jeśli strukturę można opisać jako najbliżej upakowany układ jonów tlenkowych z jonami tytanu w jednej połowie otworów oktaedrycznych? Jaka jest liczba utlenienia tytanu?
  20. Wyjaśnij, dlaczego chemicznie podobne chlorki metali alkalicznych NaCl i CsCl mają różną strukturę, podczas gdy chemicznie różne NaCl i MnS mają taką samą strukturę.
  21. Gdy minerały powstawały ze stopionej magmy, różne jony zajmowały te same miejsca w kryształach. Lit często występuje razem z magnezem w minerałach, pomimo różnicy w ładunku na ich jonach. Zaproponuj wyjaśnienie.
  22. Jodek rubidu krystalizuje z sześcienną komórką jednostkową, która zawiera jony jodkowe w narożach i jon rubidu w centrum. Jaki jest wzór tego związku?
  23. Jeden z różnych tlenków manganu krystalizuje z sześcienną komórką jednostkową, która zawiera jony manganu w narożach i w centrum. Jony tlenku znajdują się w środku każdej krawędzi komórki jednostkowej. Jaki jest wzór tego związku?
  24. NaH krystalizuje o takiej samej strukturze krystalicznej jak NaCl. Długość krawędzi sześciennej komórki jednostkowej NaH wynosi 4,880 Å.
    1. Oblicz promień jonowy H-. (Promień jonowy Li+ wynosi 0,0,95 Å.)
    2. Oblicz gęstość NaH.
  25. Jodek talu(I) krystalizuje o takiej samej strukturze jak CsCl. Długość krawędzi komórki jednostkowej TlI wynosi 4,20 Å.
    1. Oblicz promień jonowy TI+. (Promień jonowy I- wynosi 2,16 Å.)
    2. Oblicz gęstość TlI.
  26. Sześcienna komórka jednostkowa zawiera jony manganu w narożnikach i jony fluorkowe w środku każdej krawędzi.
    1. Jaki jest wzór empiryczny tego związku? Wyjaśnij swoją odpowiedź.
    2. Jaka jest liczba koordynacyjna jonu Mn3+?
    3. Oblicz długość krawędzi komórki jednostkowej, jeżeli promień jonu Mn3+ wynosi 0,65 A.
    4. Oblicz gęstość związku.
  27. Jaka jest odległość między płaszczyznami kryształu, które dyfundują promieniowanie rentgenowskie o długości fali 1,541 nm pod kątem θ równym 15,55° (odbicie pierwszego rzędu)?
  28. Dyfraktometr wykorzystujący promieniowanie rentgenowskie o długości fali 0,2287 nm wytworzył pik dyfrakcyjny pierwszego rzędu dla kąta krystalicznego θ = 16,21°. Wyznacz odstępy między płaszczyznami dyfrakcyjnymi w tym krysztale.
  29. Metal o odstępach między płaszczyznami równych 0,4164 nm dyfunduje promienie X o długości fali 0,2879 nm. Jaki jest kąt dyfrakcji dla piku dyfrakcyjnego pierwszego rzędu?
  30. Złoto krystalizuje w komórce jednostkowej w kształcie sześcianu. Odbicie drugiego rzędu (n = 2) promieniowania rentgenowskiego dla płaszczyzn tworzących wierzchołki i dna komórek jednostkowych jest pod kątem θ = 22,20°. Długość fali promieniowania X jest 1,54 Å. Jaka jest gęstość metalicznego złota?
  31. Gdy elektron w wzbudzonym atomie molibdenu spada z L do powłoki K, X-ray jest emitowany. Te X-ray są dyfraktowane pod kątem 7.75 ° przez płaszczyzny z separacji 2.64 Å. Jaka jest różnica w energii między K powłoki i L powłoki w molibdenu zakładając dyfrakcji pierwszego rzędu?
Pokaż wybrane rozwiązania

1. Struktura tego niskotemperaturowego postaci żelaza (poniżej 910 °C) jest body-centered cubic. W każdym z ośmiu rogów sześcianu znajduje się jeden ósmy atom, a w jego środku jeden atom.

3. Liczba koordynacyjna odnosi się do liczby najbliższych sąsiadów. Atom chromu leży w centrum ciała centrowanego sześcianu i ma osiem najbliższych sąsiadów (w rogach sześcianu): cztery w jednej płaszczyźnie powyżej i cztery w jednej płaszczyźnie poniżej. Liczba koordynacyjna wynosi więc osiem.

5. Najbliższe upakowanie heksagonalne występuje w ten sposób, że każdy atom dotyka 12 najbliższych sąsiadów: 6 we własnej warstwie i 3 w każdej sąsiedniej. Liczba koordynacyjna wynosi więc 12.

7. (a) W komórce sześciennej atomy metalu stykają się wzdłuż wewnętrznej przekątnej sześcianu. Przekątna wewnętrzna tworzy trójkąt prosty z krawędzią komórki i przekątną ściany. Wykorzystaj twierdzenie pitagorejskie do wyznaczenia długości przekątnej, d, na ścianie sześcianu w zależności od krawędzi, e.

d2 = e2 + e2 = 2e2

d = \sqrt{2} e

Kątna wewnętrzna sześcianu jest długością czterech promieni atomowych i można ją ponownie obliczyć wykorzystując twierdzenie pitagorejskie oraz przekątną ściany i krawędź.

begin{array}{rll}left(\ tekst{diagonalna}prawa)^2&=&d^2+e^2 \\> &=& \left(\sqrt{2} e\right)+e^2 \> &=& 2e^2+e^2 \> &=&3e^2 \\ &=& \sqrt{3}e=4rend{array}

promień wolframu = \frac{tekst{diagonal}}{4}= \frac{sqrt{3}e}{4}= \frac{sqrt{3}}{4}}left(3.165}{A}}prawa)=1.370}{A};

(b) Biorąc pod uwagę strukturę sześcienną ze środkiem ciała, każda komórka jednostkowa zawiera dwa atomy. Użyj długości krawędzi komórki jednostkowej, aby obliczyć objętość komórki jednostkowej i objętość zajmowaną przez każdy atom. Pomnóż, aby otrzymać objętość molową i podziel masę atomową przez tę wartość, aby otrzymać gęstość (e = długość krawędzi):

V(komórka) = e3 = (3,165 ∗ razy 10-8 cm)3 = 3,170 ∗ razy 10-23 cm3

V(atom) = ∗frac{3,170 ∗ razy {10}^{-23}{}}^{cm}^{3}}{}}}}}{{2 atomy}}=1.585 \times {10}^{-23}{\text{cm}}^{3}{\tekst{atom}}^{-1}

V(mol) = 1.585 \times 10-23 cm3/atom \times 6.022 \times 1023 atomy/mol

= 9.546 cm3/mol

gęstość = \frac{183,85{g mol}^{-1}}{9,546{cm}^{3}{{mol}}^{-1}} = 19,26 g/cm

9. (a) W komórce sześciennej atomy metalu są w kontakcie wzdłuż przekątnej sześcianu. Przekątna sześcianu tworzy trójkąt prosty z krawędzią komórki jednostkowej i przekątną ściany. Korzystając z twierdzenia pitagorejskiego, wyznacz długość przekątnej d na ścianie sześcianu w zależności od e.

d2 = e2 + e2 = 2e2

d = \sqrt{2} e

Krzywa sześcianu jest długością czterech promieni atomowych i można ją obliczyć ponownie korzystając z twierdzenia pitagorejskiego:

(przekątna)2 = (4r)2 = (2e)2 + e2 = 16r2 = 3e2

diagonalna = 4r = \sqrt{3}}{4}

r = \frac{\sqrt{3}}{4}} (5.025 Å) = 2.176 Å;

(b) Given a body-centered cubic structure, each unit cell contains two atoms. Użyj długości krawędzi komórki jednostkowej, aby obliczyć objętość komórki jednostkowej i objętość zajmowaną przez każdy atom. Pomnóż, aby uzyskać objętość molową i podziel gramową masę atomową przez tę wartość, aby uzyskać gęstość (e = długość krawędzi):

V (komórka) = e3 = (5,025 \times 10-8 cm)3 = 1,26884 \times 10-22 cm3

V (atom) = 1.26884 \times \frac{{10}^{-22}{\tekst{cm}^{3}{\tekst{atom}}^{\tekst{-1}}}{\tekst{2 atomy}} = 6.3442 \times 10-23 cm3

V (mol) = 6.3442 ̇ razy 10-23 cm3 ̇ razy 6,022 ̇ razy 1023 atomy/mol = 38,205 cm3

d(Ba) = ̇frac{137,33 g}{38,204 cm}^{3} = 3,595 g/cm3

11. Ze struktury krystalicznej Si wynika, że jest on mniej upakowany (liczba koordynacyjna 4) w ciele stałym niż Al (liczba koordynacyjna 12).

13. W układzie najbliżej upakowanym na każdy anion przypadają dwa otwory tetraedryczne. Jeżeli tylko połowa otworów tetraedrycznych jest zajęta, liczba anionów i kationów jest równa. Wzór dla siarczku kadmu to CdS.

15. W najbliżej upakowanym układzie jonów tlenkowych na każdy jon tlenkowy przypada jeden otwór oktaedryczny i dwa otwory tetraedryczne. Jeśli jedna połowa otworów oktaedrycznych jest wypełniona, na każde dwa jony tlenku przypada jeden jon Co. Jeżeli jedna ósma otworów tetraedrycznych jest wypełniona, na każde cztery jony tlenkowe przypada jeden jon Co. Na każde cztery jony tlenku, istnieją dwa jony Co w otworach oktaedrycznych i jeden Co w otworze tetraedrycznym; zatem wzór jest Co3O4.

17. W prostym układzie sześciennym, tylko jeden sześcienny otwór może być zajęty przez kation dla każdego anionu w układzie. Stosunek ilościowy talu do jodku musi wynosić 1:1, dlatego wzór na tal to TlI.

19. Stosunek otworów oktaedrycznych do anionów tlenu wynosi 1:1 w najbliżej upakowanym układzie. Tylko jedna połowa otworów oktaedrycznych są zajęte. Tak więc, stosunek tytanu do tlenu jest 1:2 i wzór jest TiO2. Procent masowy Ti w strukturze wynosi:

percent Ti = \frac{47,90}{47,90+text{2(15,9994)}}times \text{100%}=text{59,95%}

Liczba utlenienia tytanu wynosi +4, ponieważ na każdy jon Ti przypadają dwa jony O2-.

21. Oba jony mają zbliżone rozmiary: Mg, 0,65; Li, 0,60. To podobieństwo pozwala im dość łatwo się wymieniać. Różnica w ładunku jest na ogół kompensowana przez zamianę Si4+ na Al3+.

23. Całkowita liczba jonów Mn jest określona przez dodanie wkładów z narożników i centrum. Mn (narożniki): 8 razy \frac{1}{8}; Mn (centrum) = 1. Całkowity wkład Mn do komórki jednostkowej = 2.

Dla O, w sześcianie jest w sumie 12 krawędzi i każdy jon w krawędzi wnosi jedną czwartą do komórki jednostkowej. W związku z tym, jest 12 razy \frac{1}{4} = 3 atomy O. Stosunek Mn:O = 2:3, a wzór to Mn2O3.

27. Równanie Bragga ma postać: nλ = 2d sin θ

gdzie d jest odstępem między płaszczyznami.

d = \frac{n{lambda }}{2 sin}theta }= \frac{1(1.541 A)}{2sin15,55^{crc}}= \frac{1,541}mathring{text{A}}}{2(0,2681)} = 2,874 Å

29. \text{sin}theta = \frac{n{lambda}}{2d}= \frac{1)(0,2879\text{nm})}{(2)(0,4164)}=0,3457, więc θ = sin-1(0,3457) = 20,2°

31. Skorzystaj z równania Bragga, gdzie n = 1,

λ = 2dsinθ =2(2.64 Å)sin 7.75 = 0.712 Å

Wtedy E= θ = sin-1(6.626 razy {10}^{-34}} tekst{J s})(2.998 razy {10}^{8}{ tekst{m s}}^{-1})}{0.712 razy {10}^{-10} tekst{m}} =2.79 razy {10}^{-15} tekst{J}=1.74Times {10}^{4}text{eV}

Glossary

ciało skupione w sześcianie (BCC) ciało stałe: struktura krystaliczna, która ma sześcienną komórkę jednostkową z punktami kratowymi na rogach i w środku komórki

ciało skupione w sześcianie: najprostsza powtarzająca się jednostka kryształu sześciennego; jest to sześcian zawierający punkty kratowe w każdym rogu i w środku sześcianu

Równanie Bragga: równanie, które odnosi się do kątów, pod którymi promienie X są rozpraszane przez atomy w krysztale

liczba koordynacyjna: liczba atomów najbliżej danego atomu w krysztale lub do centralnego atomu metalu w kompleksie

cubic closest packing (CCP): struktura krystaliczna, w której płaszczyzny ściśle upakowanych atomów lub jonów są ułożone w stos jako seria trzech naprzemiennych warstw o różnych orientacjach względnych (ABC)

dyfrakcja: przekierowanie promieniowania elektromagnetycznego, które zachodzi, gdy napotyka ono fizyczną barierę o odpowiednich wymiarach

ciało stałe o strukturze sześciennej (FCC): struktura krystaliczna składająca się z sześciennej komórki jednostkowej z punktami sieciowymi na rogach i w środku każdego lica

komórka jednostkowa sześcienna o strukturze powierzchniowej: najprostsza powtarzająca się jednostka kryształu sześciennego; jest to sześcian zawierający punkty kratowe na każdym rogu i w środku każdej ściany

heksagonalne najbliższe upakowanie (HCP): struktura krystaliczna, w której ściśle upakowane warstwy atomów lub jonów są ułożone w stosy jako seria dwóch naprzemiennych warstw o różnych orientacjach względnych (AB)

otwór: (także, szczelina) przestrzeń między atomami w krysztale

izomorficzny: posiadający taką samą strukturę krystaliczną

otwór oktaedryczny: otwarta przestrzeń w krysztale w środku sześciu cząstek znajdujących się w narożach ośmiościanu

prostopadłościenna komórka jednostkowa: (także, primitive cubic unit cell) komórka jednostkowa w prostej strukturze sześciennej

simple cubic structure: struktura krystaliczna o sześciennej komórce jednostkowej z punktami kratowymi tylko w narożach

sieć przestrzenna: wszystkie punkty w krysztale, które mają identyczne środowiska

dziura tetraedryczna: przestrzeń tetraedryczna utworzona przez cztery atomy lub jony w krysztale

komórka jednostkowa: najmniejsza część siatki przestrzennej, która powtarza się w trzech wymiarach, tworząc całą siatkę

krystalografia rentgenowska: technika eksperymentalna służąca do określania odległości między atomami w krysztale poprzez pomiar kątów, pod jakimi promienie rentgenowskie ulegają dyfrakcji podczas przechodzenia przez kryształ

.

Articles