Do czego służą tablice znaków?

W tym momencie dobrym pytaniem jest: jaki jest sens uczenia się o tablicach znaków? Prosta odpowiedź jest taka, że symetria i związana z nią tabela znaków cząsteczki może być użyta do interpretacji i przewidywania wielu aspektów chemicznie istotnych spektroskopii, jak również wiązania. Zilustrujemy to następnie koncentrując się na trybach wibracyjnych cząsteczki.

W laboratorium możemy zebrać przydatne dane doświadczalne za pomocą spektroskopii w podczerwieni (IR) i Ramana. Dane te mogą być porównane z liczbą aktywnych pasm IR i/lub Ramana przewidywanych na podstawie zastosowania teorii grup i poprawnej tablicy znaków. Matematyka (teoria grup i algebra macierzy) stojąca za tym zabiegiem służy jako solidna podstawa teoretyczna. Manipulacje opisane poniżej działają, ponieważ wszystkie operacje symetrii cząsteczki tworzą grupę matematyczną i są zgodne z regułami tej grupy. Jak zauważono wcześniej, nie musimy opanować tej dziedziny matematyki, aby dobrze wykorzystać tablice znaków.

Stopnie swobody i drgania w cząsteczkach

Wstępnie omówimy tutaj stopnie swobody dla prostej cząsteczki (wody). Bardzo szybko przekonamy się, dlaczego bardzo korzystne jest stosowanie symetrii przy badaniu większych cząsteczek.

Dla cząsteczki z „N” atomów istnieje 3N stopni swobody (pamiętajmy, że żyjemy w trójwymiarowym świecie współrzędnych x, y, z). Dla cząsteczki nieliniowej 3 stopnie swobody można przypisać do translacji – ruchu ciała jako całości (Tx, Ty, Tz) i 3 do rotacji (Rx, Ry, Rz). Pozostałe ruchy atomów są przesunięciami atomów od ich średnich położeń – środek ciężkości nie ulega zmianie. Te podstawowe drgania są określane jako „tryby normalne”. Tak więc cząsteczka nieliniowa ma 3N-6 modów normalnych. Dla wody liczba trybów normalnych wynosi 3 (3 x 3 – 6 = 3). Dla cząsteczek liniowych istnieje 3N-5 trybów normalnych.

Dla wody, która oczywiście była intensywnie badana wiemy, że 3 drgania są następujące.

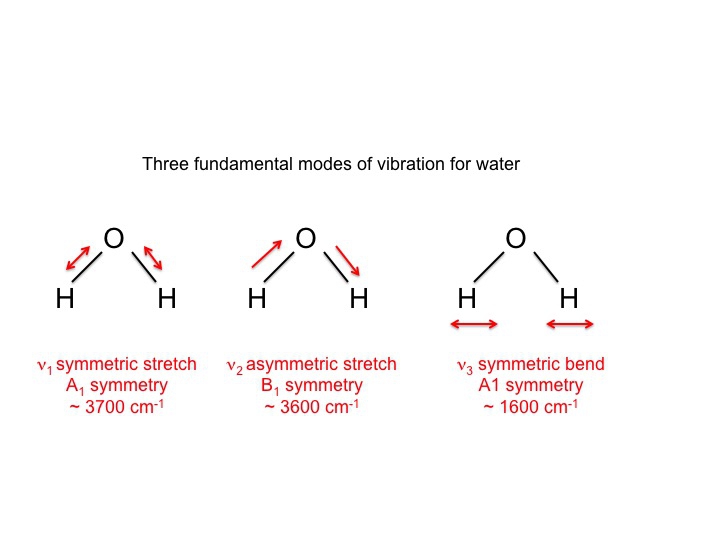
Symbole używane do opisu tych trybów (A1, B1) są tymi samymi symbolami Mullikena, z którymi spotkaliśmy się w naszej dyskusji o tablicach znaków. Innymi słowy, drgania, które są własnościami molekularnymi, mogą być opisane przez gatunki symetrii lub reprezentacje nieredukowalne. W rzeczywistości duża część literatury dotyczącej spektroskopii wibracyjnej używa tych symboli jako skróconego sposobu przekazywania informacji.

Powinno być całkiem oczywiste, że liczba drgań wzrasta gwałtownie przy nawet skromnym wzroście liczby atomów w cząsteczce. Określenie rodzajów drgań przez inspekcję (jak to zrobiliśmy dla wody) staje się teraz znacznie trudniejsze. Na przykład rozważmy następujące związki:

H2O 3 atomy 3 drgania

PH3 4 atomy 6 drgań

CO22-. 4 atomy 6 drgań

XeF4 5 atomów 9 drgań

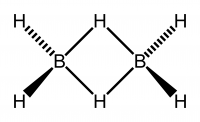
B2H6 8 atomów 18 drgań

Dla diboranu (B2H6), który ma symetrię D2h, rozgryzienie natury i gatunku symetrii wszystkich 18 drgań przez inspekcję byłoby zniechęcającym zadaniem. Jednakże, uzbrojeni w tabelę znaków dla D2h i znajomość właściwości symetrii, zadanie określenia gatunku symetrii wszystkich drgań jest proste.

W przypadku wody moglibyśmy przedstawić tabelę znaków (C2v) z 3 drganiami (ν1, v2, v3) wymienionymi w kolumnie właściwości molekularnych, jak pokazano poniżej. (ν = grecki symbol „nu”)

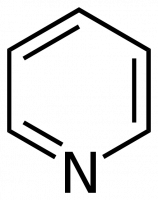
Jednakże w ogólności takie podejście jest niepraktyczne. Weźmy na przykład pirydynę (C5H5N). Grupa punktowa to również C2v, ale cząsteczka ma 11 atomów. Liczba podstawowych modów drgań wynosi 27 ( 3 x 11 – 6 = 27).

W tym przypadku musielibyśmy sporządzić tabelę postaci C2v pokazującą symetrie wszystkich 27 drgań. Z tego powodu wibracje nie są zwykle uwzględniane w tabelach znaków. Zamiast tego do użytkownika (Ciebie) należy określenie liczby i typu wibracji (zdefiniowanych przez ich gatunki symetrii) dla każdej napotkanej cząsteczki. Jak to zrobić, jest opisane poniżej.

Redukowalne reprezentacje

Jak wcześniej zauważono, jedną z ważnych właściwości tablic znaków jest to, że operacje symetrii są członkami grupy matematycznej i istnieją między nimi ważne związki. W ogóle to samo można powiedzieć o gatunkach symetrii lub nieredukowalnych reprezentacji właściwości molekularnych. Produkty ł±czenia postaci nieredukowalnych reprezentacji przez mnożenie lub dodawanie/odejmowanie również podlegaj± regułom grupy. Nowe reprezentacje nie są już najprostsze z możliwych i są określane jako „reprezentacje redukowalne”, ponieważ mogą być „zredukowane” do ich części składowych.

Na przykład, dla wody symetrie translacji (Tx, Ty, Tz) mogą być wyciągnięte bezpośrednio z tabeli znaków C2v. Są to A1, B1, i B2. Wszystkie te trzy stopnie swobody możemy przedstawić za pomocą reprezentacji ΓT i możemy zapisać poniższe wyrażenie. (Γ = wielka grecka litera „gamma”).

ΓT = A1 + B1 + B2

Wiemy, że A1, B1 i B2 są jedynie skrótowymi zapisami dla gatunków symetrii (reprezentacji nieredukowalnych). Możemy więc po prostu zapisać znaki ΓT dodając poszczególne znaki dla A1, B1 i B2 z tablicy znaków C2v.

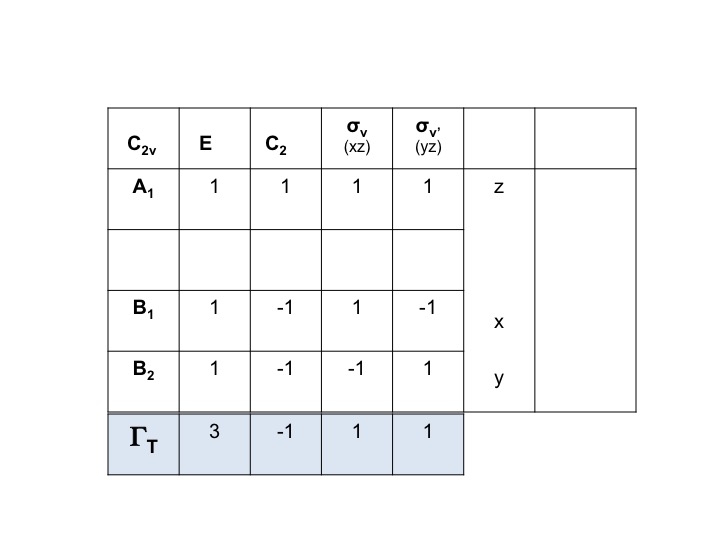
Tak więc ΓT = 3 -1 1 1.

Jest to ważna reprezentacja redukowalna i członek grupy C2v.

W podobny sposób możemy zapisać reprezentację redukowalną dla wszystkich trzech rotacji i wszystkich drgań.

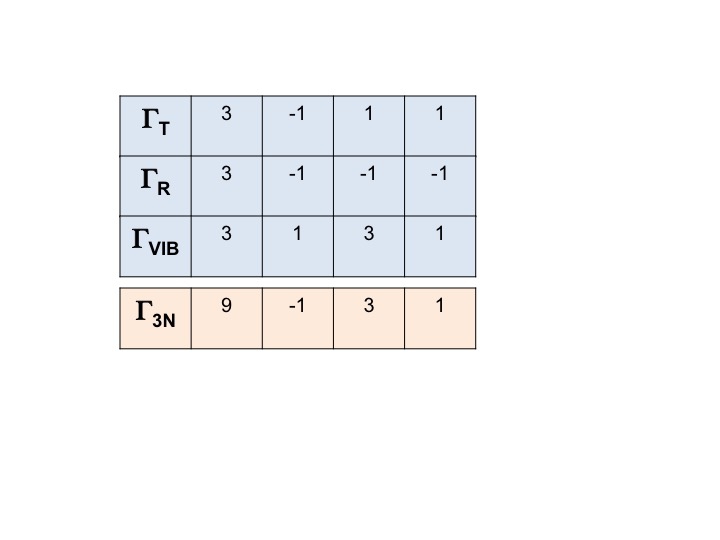
Odwzorowanie dla WSZYSTKICH stopni swobody dla cząsteczki (3N) możemy zapisać jako

Γ3N = ΓT + ΓR + ΓVIB

a redukowalne odwzorowanie dla niej otrzymujemy po prostu sumując znaki dla ΓT, ΓR i ΓVIB.

Γ3N = 9 -1 3 1

Zapamiętaj to – pojawi się później!

Aczkolwiek zbiór znaków 9 -1 3 1 jest ważnym członkiem grupy C2v, nie jest on szczególnie użyteczny przy omawianiu własności molekularnych. To, co jest naprawdę potrzebne, to język skrótów gatunków symetrii (symbole Mullikena, A1, B1 itd.). Innymi słowy, chcemy wyrazić Γ3N w kategoriach A1, B1 itd. Z informacji podanych powyżej można łatwo pokazać przez inspekcję, że:

Γ3N = 3A1 +A2 + 3B1 +2B2

Dobra wiadomość jest taka, że dla innych bardziej złożonych cząsteczek nie musimy wykonywać tego zadania przez inspekcję, ponieważ:

1. Możemy łatwo wygenerować Γ3N jako redukowalną reprezentację dla cząsteczki (jeśli znamy jej symetrię grupy punktowej).

2. Możemy łatwo przekształcić redukowalną reprezentację Γ3N w sumę jej gatunków symetrii (symbole Mullikena) używając „prostego” wzoru znanego jako wzór redukcyjny.

Ogólna metoda otrzymywania Γ3N

Krok 1

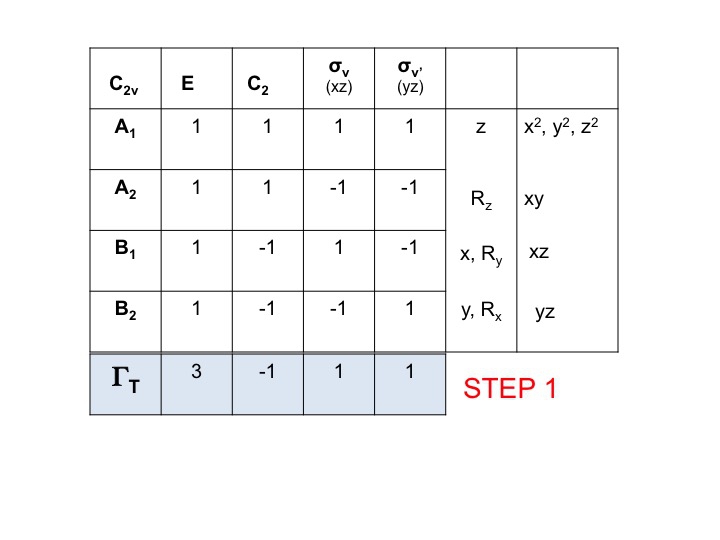
Przyjmij tabelę znaków dla cząsteczki i dodaj wiersz na dole. W tym wierszu generujemy redukowalną reprezentację dla ΓT (lub Γxyz), tak jak zrobiliśmy to powyżej, po prostu dodając znaki dla każdej operacji, które odpowiadają właściwościom molekularnym dla x, y i z. Dla C2v pokazaliśmy już, że są to znaki odpowiadające A1, B1 i B2.

Krok 2

Dodaj kolejny wiersz poniżej ΓT i zapisz liczbę atomów, które NIE ZMIENIAJĄ swojego położenia podczas każdej operacji symetrii. W tym momencie uświadamiamy sobie jak użyteczny jest prawdziwy zestaw modeli molekularnych. Aby to zrobić, musisz również wiedzieć, gdzie znajdują się elementy symetrii i jak operacje symetrii wpływają na cząsteczkę. Oczywiście, już wiesz jak to zrobić, ponieważ studiowałeś notację Schönfliesa i wiesz jak przypisać grupę punktową cząsteczki. Tabela znaków ma również wszystkie operacje symetrii wymienione według klas w górnym rzędzie.

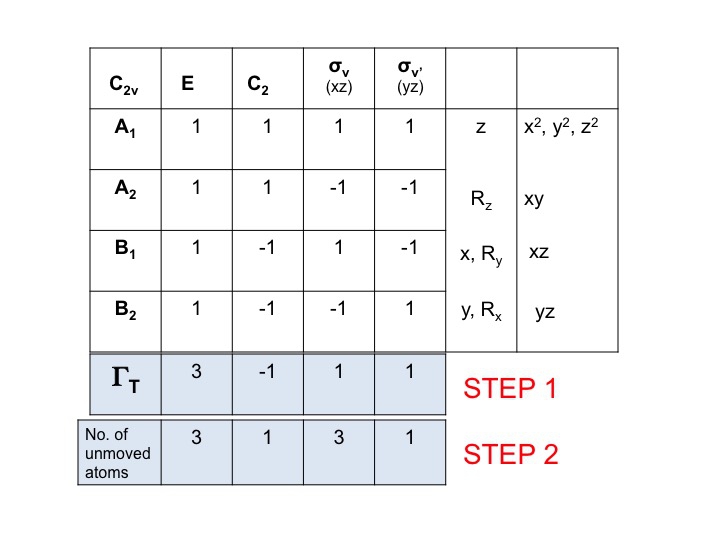
Tak więc dla wody (3 atomy) pod E są 3 nieporuszone atomy, ale dla C2 oba atomy H poruszają się, ale ponieważ atom O siedzi na osi C2 nie zmienia swojego położenia, więc zapisujemy 1 pod kolumną C2. Nowy zbiór liczb wygenerowany w kroku 2 (3 1 3 1) jest również redukowalną reprezentacją w C2v i spełnia reguły grupy.

Krok 3

W tym kroku po prostu mnożymy razem znaki, które zostały wygenerowane w krokach 1 i 2. Wynik (trzeci rząd) jest redukowalną reprezentacją dla Γ3N (lub ΓTOT). To takie proste.

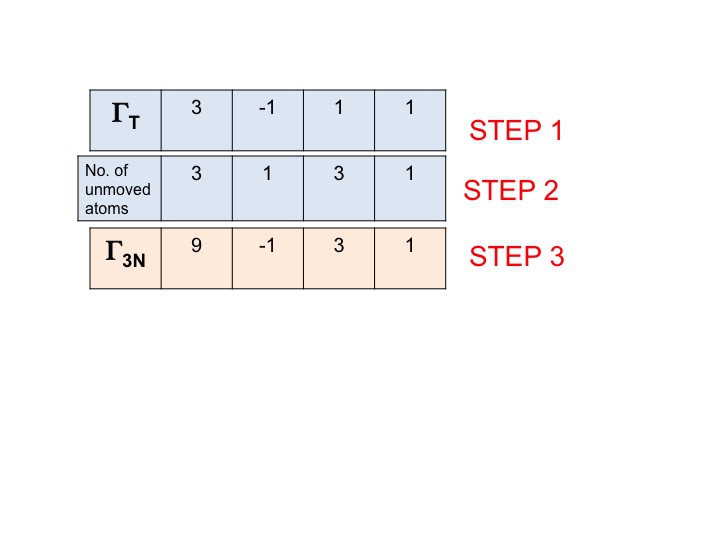
Zauważ, że nowa redukowalna reprezentacja (9 -1 1 3) jest identyczna z reprezentacją dla Γ3N, którą otrzymaliśmy wcześniej przez inspekcję.

Redukcja reprezentacji redukowalnej

Aby przekształcić KAŻDĄ reprezentację redukowalną w sumę jej reprezentacji nieredukowalnych (gatunków symetrii lub symboli Mullikena) używamy formuły redukcyjnej:

Możesz łatwo znaleźć tę informację w tabeli znaków:

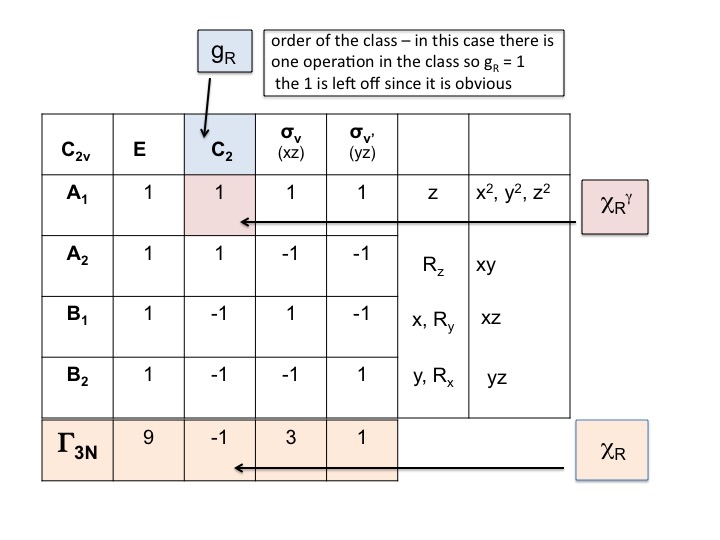
Powracając do naszego przykładu dla wody: Grupa punktowa C2v, rząd (g) = 4

Oprezentacja redukowalna dla Γ3N = 9 -1 3 1

Liczba wystąpień A1 w tej reprezentacji wynosi zatem

aA1 = 1/4 { 1.1.9 + 1.1. (-1) + 1.1.3 +1.1.1} = 3

więc Γ3N zawiera 3 gatunki o symetrii A1. Liczbę pozostałych gatunków symetrycznych obliczamy następująco:

aA2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1).3 + 1.(-1).1 } = 1 jeden A2 obecny

aB1 = 1/4 { 1.1.9 + 1.(-1).(-1) + 1.1.3 + 1.(-1).1} = 3 3 B1 obecny

aB2 = 1/4 {1.1.9 + 1.(-1)(-1) + 1.(-1).3 + 1.1.1} = 2 2 B2 obecny

Możemy teraz napisać Γ3N = 3A1 + A2 + 3B1 + 2B2 (dokładnie to, co otrzymaliśmy przez „inspekcję” powyżej. Możemy teraz odjąć gatunki symetrii dla translacji i rotacji, a to da nam liczbę i gatunki symetrii podstawowych modów drgań. ΓT i ΓR można otrzymać bezpośrednio z tabeli znaków.

Γ3N = 3A1 + A2 + 3B1 + 2B2

ΓT = A1 + B1 + B2

ΓR = A2 + B1 + B2

ΓVIB = Γ3N -. ΓT – ΓR = 2A1 +B1

Trzy normalne tryby drgań dla wody mają symetrie A1, A1 i B1.

Mamy teraz ogólną metodę określania wszystkich podstawowych trybów drgań dla cząsteczki i wyrażania tych trybów w skróconym języku symboli Mullikena. Jest to jedno z ćwiczeń, które będzie sprawdzane na egzaminie 1. Najlepszym sposobem, aby nabrać pewności w tej metodzie jest przećwiczenie jak największej liczby możliwych przykładów!

Następne: Reguły wyboru

.