Minder…
Een Pythagoreïsch drietal is een drietal positieve gehele getallen 
, 
, en 
zodat er een rechthoekige driehoek bestaat met benen 
en hypotenusa 
. Door de stelling van Pythagoras is dit gelijk aan het vinden van positieve gehele getallen 
, 
, en 
die voldoen aan
 |
(1)
|
De kleinste en bekendste Pythagoras-driehoek is 
. De rechthoekige driehoek met deze zijlengten wordt ook wel de 3,4,5 driehoek genoemd.
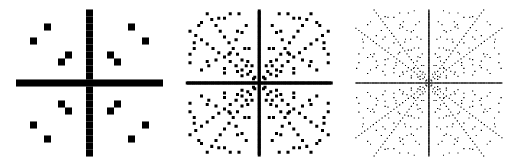
Plots van punten in het 
-vlak zo dat 
een Pythagoreïsch drievoud is zijn hierboven weergegeven voor opeenvolgende grotere grenswaarden. Deze kavels bevatten negatieve waarden van 
en 
, en zijn daarom symmetrisch om zowel de x- als de y-as.
Ook kavels van punten in het 
-vlak zodanig dat 
een Pythagoreïsch drievoud is, zijn hierboven weergegeven voor opeenvolgende grotere grenzen.
Het is gebruikelijk om alleen primitieve Pythagoras-driehoeken (ook wel “gereduceerde” driehoeken genoemd) te beschouwen waarin 
en 
relatief priem zijn, omdat andere oplossingen triviaal uit de primitieve kunnen worden gegenereerd. De primitieve driehoeken zijn hierboven afgebeeld, en het is onmiddellijk te zien dat de radiaallijnen die corresponderen met imprimitieve driehoeken in de oorspronkelijke plot in deze figuur ontbreken. Voor primitieve oplossingen moet één van 
of 
even zijn, en de andere oneven (Shanks 1993, p. 141), waarbij 
altijd oneven is.
En bovendien is een zijde van elk Pythagoreïsch drietal deelbaar door 3, een andere door 4, en weer een andere door 5. Een zijde kan twee van deze delers hebben, zoals in (8, 15, 17), (7, 24, 25), en (20, 21, 29), of zelfs alle drie, zoals in (11, 60, 61).
Gegeven een primitief drievoud 
, worden drie nieuwe primitieve driehoeken verkregen uit
 |
 |
 |
(2)
|
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
waar
 |
 |
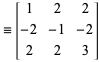(5)
|
 |
 |
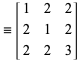(6)
|
 |
 |
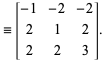(7)
|
Hall (1970) en Roberts (1977) bewijzen dat 
een primitief Pythagoreïsch drietal is alsf
 |
(8)
|
waar 
een eindig product is van de matrices 
, 
, 
. Hieruit volgt dat elk primitief Pythagoreïsch drietal lid moet zijn van de oneindige matrix
 |
(9)
|
Pythagoras en de Babyloniërs gaven een formule voor het genereren van (niet noodzakelijk primitieve) driehoeken als
 |
(10)
|
voor 
, die een verzameling verschillende driehoeken genereert die noch alle primitieve, noch alle imprimitieve driehoeken bevat (en waarbij in het speciale geval 
, 
).
De vroege Grieken gaven
 |
(11)
|
waar 
en 
relatief priem zijn en van tegengestelde pariteit (Shanks 1993, p. 141), die een verzameling onderscheiden driehoeken genereert die precies de primitieve driehoeken bevat (na gepaste sortering 
en 
).
Laat 
een Fibonacci-getal zijn. Dan
 |
(12)
|
genereert verschillende Pythagoras-driehoeken (Dujella 1995), zij het niet uitputtend voor zowel primitieve als imprimitieve driehoeken. Meer algemeen, uitgaande van positieve gehele getallen 
, 
, en het construeren van de Fibonacci-achtige rij 
met termen 
, 
, 
, 
, 
, … genereert verschillende Pythagoras-driehoeken
 |
(13)
|
(Horadam 1961), waarbij
 |
(24)
|
(Beiler 1966, p. 116). Merk op dat 
alsf 
een priemgetal is of tweemaal een priemgetal. De eerste paar getallen voor 
, 2, … zijn 0, 0, 1, 1, 1, 1, 2, 2, 1, 1, 4, 1, … (OEIS A046079).
Om het aantal manieren 
te vinden waarop een getal 
de schuine zijde van een primitieve rechthoekige driehoek kan zijn, schrijft u de factorisatie als
 |
(25)
|
waarbij de 
s de vorm 
hebben en de 
s de vorm 
. Het aantal mogelijke primitieve rechthoekige driehoeken is dan
 |
(26)
|
Voorbeeld, 
aangezien
 |
 |
 |
(27)
|
 |
 |
 |
(28)
|
De waarden van 
voor 
, 2, … zijn 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, … (OEIS A024362). De eerste paar priemgetallen van de vorm 
zijn 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, … (OEIS A002144), dus de kleinste zijlengtes die de hypotenen zijn van 1, 2, 4, 8, 16, … primitieve rechthoekige driehoeken zijn 5, 65, 1105, 32045, 1185665, 48612265, … (OEIS A006278).
Het aantal mogelijke primitieve of niet-primitieve rechthoekige driehoeken met 
als schuine zijde is
 |
 |
 |
(29)
|
 |
 |
 |
(30)
|
(correctie van de typefout van Beiler 1966, p. 117, waarin staat dat deze formule alleen het aantal niet-primitieve oplossingen geeft), waarbij 
de som van de kwadratenfunctie is. Er zijn bijvoorbeeld vier verschillende gehele driehoeken met schuine zijde 65, omdat
 |
(31)
|
De eerste paar getallen voor 
, 2, … zijn 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, … (OEIS A046080). De kleinste hypotenussen met 
verschillende driehoeken zijn 1, 5, 25, 125, 65, 3125, … (OEIS A006339). De volgende tabel geeft de hypotenussen waarvoor er precies 
verschillende rechte gehele driehoeken bestaan voor 
, 1, …, 5.
 |
OEIS | hypotenussen waarvoor er  verschillende gehele driehoeken bestaan |
| 0 | A004144 | 1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, … |
| 1 | A084645 | 5, 10, 13, 15, 17, 20, 26, 29, 30, 34, 35, … |
| 2 | A084646 | 25, 50, 75, 100, 150, 169, 175, 200, 225, … |
| 3 | A084647 | 125, 250, 375, 500, 750, 875, 1000, 1125, 1375, … |
| 4 | A084648 | 65, 85, 130, 145, 170, 185, 195, 205, 221, 255, …. |
| 5 | A084649 | 3125, 6250, 9375, 12500, 18750, 21875, 25000, … |
Het totaal aantal manieren waarop 
hetzij een been hetzij een schuine zijde van een rechthoekige driehoek kan zijn, wordt dus gegeven door
 |
(32)
|
De waarden voor 
, 2, … zijn 0, 0, 1, 1, 2, 1, 1, 2, 2, 2, 1, 4, 2, 1, 5, 3, … (OEIS A046081). De kleinste getallen 
die de zijden kunnen zijn van 
algemene rechthoekige driehoeken voor 
, 2, … zijn 3, 5, 16, 12, 15, 125, 24, 40, … (OEIS A006593; Beiler 1966, p. 114).
Er zijn 50 Pythagoreïsche driehoeken met schuine zijde kleiner dan 100, waarvan de eerste, gesorteerd op oplopende 
, zijn (3, 4, 5), (6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083, A046084, en A009000).
Van deze zijn er slechts 16 primitieve drietallen met een schuine zijde kleiner dan 100: (3, 4,5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65), (16, 63, 65), (48, 55, 73), (36, 77, 85), (13, 84, 85), (39, 80, 89), en (65, 72, 97) (OEIS A046086, A046087, en A020882).
Laat het aantal driehoeken 
zijn, het aantal driehoeken 
, en het aantal primitieve driehoeken kleiner dan 
zijn. Dan geeft de volgende tabel een overzicht van de waarden voor machten van 10.
 |
OEIS |  ,  , … |
 |
A101929 | 1, 50, 878, 12467, … |
 |
A101930 | 2, 52, 881, 12471, … |
 |
A101931 | 1, 16, 158, 1593, … |
Lehmer (1900) bewees dat het aantal primitieve oplossingen met een schuine zijde kleiner dan 
voldoet aan
 |
(33)
|
(OEIS A086201).
De inradii van de eerste paar primitieve Pythagoras-driehoeken gerangschikt naar oplopend 
worden gegeven door 1, 2, 3, 3, 6, 5, 4, 10, 5, … (OEIS A014498).
Er is een algemene methode om drietallen van Pythagoreïsche driehoeken met gelijke oppervlakte te verkrijgen. Neem de drie verzamelingen van generatoren als
 |
 |
 |
(34)
|
 |
 |
 |
(35)
|
 |
 |
 |
(36)
|
 |
 |
 |
(37)
|
 |
 |
 |
(38)
|
 |
 |
 |
(39)
|
Dan is de rechterdriehoek gegenereerd door elk drietal (
) heeft een gemeenschappelijke oppervlakte
 |
(40)
|
(Beiler 1966, pp. 126-127). Het enige extremum van deze functie ligt bij 
. Daar 
voor 
, is de kleinste oppervlakte gedeeld door drie niet-primitieve rechthoekige driehoeken gegeven door 
, hetgeen een oppervlakte oplevert van 840 en overeenkomt met de driehoeken (24, 70, 74), (40, 42, 58), en (15, 112, 113) (Beiler 1966, p. 126).
Rechter driehoeken waarvan de oppervlakte uit één enkel cijfer bestaat zijn onder andere 
(oppervlakte van 6) en 
(oppervlakte van 666666; Wells 1986, p. 89).
In 1643 daagde Fermat Mersenne uit om een Pythagoreïsch drietal te vinden waarvan de schuine zijde en de som van de benen kwadraten waren. Fermat vond de kleinste oplossing:
 |
 |
 |
(41)
|
 |
 |
 |
(42)
|
 |
 |
 |
(43)
|
met
 |
 |
 |
(44)
|
 |
 |
 |
(45)
|
Een verwant probleem is te bepalen of een bepaald geheel getal 
de oppervlakte kan zijn van een rechthoekige driehoek met rationale zijden. 1, 2, 3 en 4 zijn geen oppervlakten van een rationale driehoek, maar 5 wel (3/2, 20/3, 41/6), net als 6 (3, 4, 5). De oplossing van het probleem betreft de elliptische kromme
 |
(46)
|
Een oplossing (
, 
, 
) bestaat als (46) een rationele oplossing heeft, in welk geval
 |
 |
 |
(47)
|
 |
 |
 |
(48)
|
(Koblitz 1993). Er is geen algemene methode bekend om te bepalen of er een oplossing is voor willekeurige 
, maar met een techniek die in 1983 door J. Tunnell is bedacht, kunnen bepaalde waarden worden uitgesloten (Cipra 1996).