Een groeiend interessegebied voor wetenschappers die het belang, de macht of de invloed tussen entiteiten onderzoeken, wordt de grafiektheorie genoemd. De wortels van de grafentheorie liggen in 1736, toen de wiskundige Carl Ehler Leonhard Euler inleidde in het probleem van de bruggen van Konigsberg.
Het probleem van de bruggen van Konigsberg is gebaseerd op de voormalige Duitse stad Konigsberg, die aan weerszijden van de rivier de Pregel ligt. In het centrum lagen twee grote eilanden die met elkaar en met de rivieroevers verbonden waren door zeven bruggen. Carl Ehler werd geobsedeerd door het vinden van een route om door elk van de zeven bruggen te lopen zonder over een van hen meer dan één keer te lopen. Ehler nam contact op met Leonhard Euler, een Zwitserse wiskundige. Euler bevestigde Ehlers hypothese dat het probleem geen oplossing had, en Eulers uitleg leidde tot een nieuw wiskundig paradigma, genaamd Geometrie van Positie.
Eulers nieuwe geometrieparadigma stelde dat de locatie van de bruggen er niet toe deed. In plaats daarvan kan het probleem worden vereenvoudigd door van elke brug een punt (knoop) te maken met lijnen (randen) om de verbindingen tussen de bruggen weer te geven. Deze praktijk van het gebruik van knooppunten en randen staat nu bekend als Graph Theory.
U kunt hier meer lezen over het probleem Bridges in Konigsberg.
In eerste instantie had Graph Theory niet veel nut bij het oplossen van problemen en stond het niet hoog aangeschreven bij wiskundigen. Moderne computerkracht om grote permutaties te verwerken heeft de principes van de Graph Theory echter praktischer gemaakt. In dit artikel leert u de principes van de grafentheorie toe te passen op analyses die op Python zijn gebaseerd.


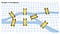
Niet alle netwerken in een grafisch systeem zijn onderling met elkaar verbonden. Deze ontkoppeling ontstaat wanneer componenten worden gevormd. Zoals in onderstaande grafiek te zien is, wordt een component pas gevormd als elk knooppunt een pad naar andere knooppunten heeft.
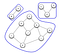
Applied Graph Theory in Python
In Python wordt networkx vaak gebruikt voor toegepaste grafentheorie ook wel bekend als netwerkanalyse . Het pakket heeft handige functionaliteit om snel de karakteristieken van een grafiek samen te vatten. U kunt de onderstaande stappen bekijken en meelopen terwijl we een grafiek maken en de opbouw ervan begrijpen.
De onderstaande code maakt eerst een leeg grafiekobject P. De volgende stappen voegen knooppunten toe en beschrijven de randen.
Argumenten zoals <object>.nodes() of <object>.edges() zijn snelle manieren om alle knooppunten en randen van het grafieksysteem te bekijken.
print(P.nodes())print(P.edges())
Tot slot wordt nx.draw gebruikt om het netwerk te visualiseren.
%matplotlib inline
import matplotlib.pyplot as plt
nx.draw(P, with_labels = True)
Oefeningen 1:
Nu de basisbegrippen van grafieken zijn besproken, zijn de volgende oefeningen een goede methode om te oefenen:
- Hoeveel knooppunten zitten er in de bovenstaande grafiek?
- Hoeveel ribben zitten er in bovenstaande grafiek?
- Wat is de geodeet voor E en C?
- Zijn er meer dan 1 component in de grafiek?
Hoeveel echte gegevens gebruiken?
De oefening hieronder maakt gebruik van gegevens over vluchten binnen de Verenigde Staten in 2015. De dataset bevat herkomst- en bestemmingsluchthavens, naast attributen die de vlucht beschrijven, waaronder vliegtijd en vertragingen (weers-, veiligheids- of luchtvaartmaatschappijgerelateerd).
Omdat de dataset groot is, zal de oefening zich concentreren op vluchten afkomstig van luchthavens in de omgeving van Los Angeles (Los Angeles (LAX), Burbank (BUR), Orange County (SNA) en San Bernardino County (ONT)). Bovendien zal de focus liggen op vluchten die lijken op mijn Deloitte reisschema – vliegen op zondag en terug op donderdag.
Omdat we al herkomst en bestemming gegevens hebben, **** velden ORIGIN_AIRPORT en DESTINATION_AIRPORT zullen dienen als bronvelden voor nodes en edges – er is geen noodzaak om nodes of edges te creëren zoals we deden in de eerste oefening. Zodra nodes zijn gedefinieerd, zal <object>.edges() alle paarsgewijze relaties tussen hen verschaffen. Tenslotte zal nx.draw helpen om een grafiek te maken van de randen.

FG.edges()

nx.draw(FG, with_labels = True)

In de bovenstaande uitvoer, zijn de knooppunten gelabeld met luchthavencodes. Alle verbindingen leiden naar één van de vier luchthavens in de omgeving van Los Angeles, omdat deze vier de enige waren die voor deze oefening zijn geselecteerd. Los Angeles International (LAX) is de grootste luchthaven van de vier en de grafiek laat duidelijk zien dat veel steden alleen bereikbaar zijn via LAX en niet via andere, kleinere luchthavens. Dit toont de verbondenheid, of graad centraliteit, van LAX. In networkx wordt nx.algorithms.degree_centrality(<object>) **** gebruikt om de centraliteit van elk knooppunt in het grafieksysteem te vinden.
# Calculating the centrality of each of the airports
nx.algorithms.degree_centrality(FG)
We kunnen meer granulair te werk gaan en een korte ‘for loop’ gebruiken om randen tussen twee gebieden van belang te produceren. De volgende code wordt bijvoorbeeld gebruikt om alle mogelijke vluchten van San Bernardino County (ONT) naar Newark (EWR) op zondag of donderdag te vinden.
Van de verschillende vluchtopties tussen San Bernardino County en Newark kan de nx.dijkstra_path worden gebruikt om het Euclidische pad (of het kortste pad) te vinden.
#Finding the dijkstra path
djk_path = nx.dijkstra_path(FG, source='ONT', target='EWR')
djk_path
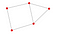
Oefening 2:
- Maak de volgende grafiek met behulp van
nx.draw(). Let op: uw netwerk ziet er misschien niet precies hetzelfde uit, maar de paden, randen en knooppunten moeten overeenkomen met het onderstaande netwerk. - Print alle randen.
- Wat is het kortste pad van L naar F?
