Alfa-polonium kristalliseert in een eenvoudige kubische eenheidscel:

1. Twee aangrenzende Po atomen raken elkaar, dus de randlengte van deze cel is gelijk aan twee Po atomaire stralen: l=2r. De straal van Po is dus r=2r=2r = 336 pm}{2}=168 pm}.
2. De dichtheid wordt gegeven door =dichtheid}=massa}{volume}. De dichtheid van polonium kan worden gevonden door de dichtheid van zijn eenheidscel te bepalen (de massa in een eenheidscel gedeeld door het volume van de eenheidscel). Aangezien een Po eenheidscel op elk van zijn acht hoeken een achtste van een Po atoom bevat, bevat een eenheidscel één Po atoom.

De massa van een Po eenheidscel kan worden gevonden door:

\text{1 Po eenheidscel}\times \dfrac{1 Po atoom}{\text{1 Po eenheidscel}}\times \dfrac{1 mol Po}}{6.022 maal 1023 Po atomen} maal 208,998 g 1 mol Po}=3.47 maal {10}^{-22}}^{g}

Het volume van een Po eenheidscel kan worden gevonden door:

V={l}^{3}={(336 maal {10}^{-10}}}^{3}=3.79 maal {10}^{-23}{tekst{cm}}^{3}

(Merk op dat de randlengte is omgerekend van pm naar cm om de gebruikelijke volume-eenheden voor de dichtheid te krijgen.)

Daaruit volgt de dichtheid van {Po}={3.471 maal {10}^{-22}^text{g}{3,79 maal {10}^{-23}{cm}}^{3}={9,16 g/cm}^{3}

Figuur 5. Kubische eenheidscellen van metalen tonen (in de bovenste figuren) de plaatsen van de roosterpunten en (in de onderste figuren) de metaalatomen die zich in de eenheidscel bevinden.

Figuur 6. In een lichaamsgecentreerde kubusstructuur raken atomen in een bepaalde laag elkaar niet. Elk atoom raakt vier atomen in de laag erboven en vier atomen in de laag eronder.

Figuur 7. Een face-centered cubic solid heeft atomen op de hoeken en, zoals de naam al aangeeft, in de middelpunten van de vlakken van zijn eenheidscellen.

Figuur 8. Een CCP-opstelling bestaat uit drie zich herhalende lagen (ABCABC…) van hexagonaal gerangschikte atomen. Atomen in een CCP-structuur hebben een coördinatiegetal van 12, omdat ze contact maken met zes atomen in hun laag, plus drie atomen in de laag erboven en drie atomen in de laag eronder. Door ons perspectief te draaien, kunnen we zien dat een CCP-structuur een eenheidscel heeft met een vlak dat een atoom van laag A in een hoek bevat, atomen van laag B over een diagonaal (op twee hoeken en in het midden van het vlak), en een atoom van laag C in de overgebleven hoek. Dit is hetzelfde als een face-centered cubic arrangement.

Figuur 9. In beide types zijn de atomen zo compact mogelijk ingepakt. De zeshoekige dichtste pakking bestaat uit twee alternerende lagen (ABABAB…). Kubische dichtste verpakking bestaat uit drie afwisselende lagen (ABCABCABC…).

Voorbeeld 2: Berekening van atoomstraal en dichtheid voor metalen, deel 2

Calcium kristalliseert in een face-centered kubische structuur. De randlengte van de eenheidscel is 558,8 pm.

1. Wat is de atoomstraal van Ca in deze structuur?
2. Bereken de dichtheid van Ca.

Toon oplossing

Deel 1

In een FCC-structuur komen Ca-atomen met elkaar in contact over de diagonaal van het vlak, zodat de lengte van de diagonaal gelijk is aan vier Ca-atomaire stralen (d = 4r). Twee aangrenzende zijden en de diagonaal van het vlak vormen een rechthoekige driehoek, waarbij de lengte van elke zijde gelijk is aan 558,8 pm en de lengte van de schuine zijde gelijk is aan vier Ca atomaire stralen:

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}^{2}}}}} {(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}={(4r)}^{2}

Solving this gives r=\sqrt{\dfrac{{(558.8\text{pm})}^{2}+{(558.5{text{pm})}^{2}}{16}={197,6 pmg voor een Ca-straal}.

Deel 2

De dichtheid wordt gegeven door {text{dichtheid}=\dfrac{text{massa}}{{volume}}. De dichtheid van calcium kan worden gevonden door de dichtheid van zijn eenheidscel te bepalen: bijvoorbeeld de massa in een eenheidscel gedeeld door het volume van de eenheidscel. Een gecentreerde eenheidscel van Ca heeft op elk van de acht hoeken een achtste atoom (8 maal 1 atoom) en op elk van de zes vlakken een half atoom (6 maal 1 atoom), dus in totaal vier atomen in de eenheidscel.

De massa van de eenheidscel kan worden gevonden door:

Eenheidscel van Ca} maal \dfrac{4 Ca atomen}{eenheidscel van Ca} maal \dfrac{1 mol Ca}{6.6. De hoeveelheid Ca-atomen in de cel is ongeveer 40,078 maal 40,078 maal 40,078 maal 40,078 maal 40,078 maal 40,078 maal 40,078 maal 1 mol Ca}}=2.662 maal {10}^{-22}^{g}

Het volume van een Ca-eenheidscel kan worden gevonden door:

V={a}^{3}={(558,8 maal {10}^{-10}^{cm})}^{3}=1.745 maal {10}^{-22}{10}^{cm}}^{3}

(Merk op dat de randlengte is omgerekend van pm naar cm om de gebruikelijke volume-eenheden voor de dichtheid te krijgen.)

Dan is de dichtheid van Ca=2,662 maal 10}^{-22}g}1,745 maal 10}^{-22}cm}^{3}= 1,745 maal 10}^{-22}cm}^{3}= 1,662 maal 10}^{22}g}^{1,745 maal 10}^{22}cm}^{3}}53 g/cm}}^{3}

Check Your Learning

Zilver kristalliseert in een FCC-structuur. De randlengte van de eenheidscel is 409 pm.

1. Wat is de atoomstraal van Ag in deze structuur?
2. Bereken de dichtheid van Ag.

In het algemeen wordt een eenheidscel gedefinieerd door de lengten van drie assen (a, b, en c) en de hoeken (α, β, en γ) ertussen, zoals geïllustreerd in figuur 10. De assen zijn gedefinieerd als de lengtes tussen punten in het ruimtelrooster. Bijgevolg verbinden de eenheidscelassen punten met identieke omgevingen.

Figuur 10. Een eenheidscel wordt gedefinieerd door de lengten van de drie assen (a, b, en c) en de hoeken (α, β, en γ) tussen de assen.

Er zijn zeven verschillende roostersystemen, waarvan sommige meer dan één type rooster hebben, voor een totaal van veertien verschillende eenheidscellen, die de in figuur 11 getoonde vormen hebben.

Figuur 11. Er zijn zeven verschillende roostersystemen en 14 verschillende eenheidscellen.

De structuren van Ionische kristallen

Ionische kristallen bestaan uit twee of meer verschillende soorten ionen die gewoonlijk verschillende afmetingen hebben. De verpakking van deze ionen in een kristalstructuur is complexer dan de verpakking van metaalatomen die dezelfde grootte hebben.

De meeste mono-atomaire ionen gedragen zich als geladen bollen, en hun aantrekkingskracht op ionen met tegengestelde lading is in elke richting hetzelfde. Bijgevolg ontstaan stabiele structuren voor ionische verbindingen (1) wanneer ionen met één lading door zoveel mogelijk ionen met de tegengestelde lading worden omgeven en (2) wanneer de kationen en anionen met elkaar in contact zijn. De structuur wordt bepaald door twee belangrijke factoren: de relatieve grootte van de ionen en de verhouding tussen het aantal positieve en negatieve ionen in de verbinding.

Figuur 12. Kationen kunnen twee soorten gaten tussen anionen bezetten: octahedrale gaten of tetrahedrale gaten.

In eenvoudige ionische structuren vinden we gewoonlijk de anionen, die gewoonlijk groter zijn dan de kationen, gerangschikt in een dicht bij elkaar liggende rij. (Zoals eerder gezien, maken extra elektronen die worden aangetrokken door dezelfde kern de anionen groter en minder elektronen die worden aangetrokken door dezelfde kern maken de kationen kleiner in vergelijking met de atomen waaruit zij zijn gevormd). De kleinere kationen bezetten gewoonlijk een van de twee soorten gaten (of tussenruimten) die tussen de anionen overblijven. De kleinste van de gaten bevindt zich tussen drie anionen in één vlak en één anion in een aangrenzend vlak. De vier anionen die dit gat omgeven zijn gerangschikt op de hoeken van een tetraëder, zodat het gat een tetraëdergat wordt genoemd. Het grotere type gat bevindt zich in het centrum van zes anionen (drie in één laag en drie in een aangrenzende laag) die zich op de hoeken van een octaëder bevinden; dit wordt een octaëdervormig gat genoemd. Figuur 12 illustreert beide soorten gaten.

Afhankelijk van de relatieve grootte van de kationen en anionen, kunnen de kationen van een ionische verbinding tetrahedrale of octahedrale gaten bezetten, zoals geïllustreerd in figuur 13. Relatief kleine kationen bezetten tetrahedral gaten, en grotere kationen bezetten octahedral gaten. Als de kationen te groot zijn om in de octahedrale gaten te passen, kunnen de anionen een meer open structuur aannemen, zoals een eenvoudige kubische array. De grotere kationen kunnen dan de grotere kubische gaten bezetten die door de meer open ruimte mogelijk worden gemaakt.

Figuur 13. De grootte van een kation en de vorm van het gat dat door de verbinding wordt ingenomen, staan in direct verband met elkaar.

Er zijn twee tetrahedrale gaten voor elk anion in een HCP- of CCP-array van anionen. Een verbinding die kristalliseert in een dicht opeen gepakte array van anionen met kationen in de tetrahedral gaten kan een maximum kation:anion verhouding van 2:1 hebben; alle van de tetrahedral gaten worden gevuld bij deze verhouding. Voorbeelden zijn Li2O, Na2O, Li2S, en Na2S. Verbindingen met een verhouding van minder dan 2:1 kunnen ook kristalliseren in een dicht bij elkaar liggende rij van anionen met kationen in de tetrahedrale gaten, als de ionische maten passen. In deze verbindingen blijven echter enkele van de tetrahedrale gaten vacant.

De verhouding van octahedrale gaten tot anionen in een HCP- of CCP-structuur is 1:1. Verbindingen met kationen in octahedrale gaten in een dicht opeen gepakte reeks van anionen kunnen dus een maximale kation:anion verhouding van 1:1 hebben. In NiO, MnS, NaCl, en KH, bijvoorbeeld, zijn alle octahedrale gaten gevuld. Verhoudingen van minder dan 1:1 worden waargenomen wanneer sommige van de octahedrale gaten leeg blijven.

In een eenvoudige kubische array van anionen is er voor elk anion in de array één kubisch gat dat door een kation kan worden bezet. In CsCl, en in andere verbindingen met dezelfde structuur, zijn alle kubische gaten bezet. In SrH2, UO2, SrCl2, en CaF2 is de helft van de kubische gaten bezet.

Verschillende soorten ionische verbindingen kristalliseren vaak in dezelfde structuur wanneer de relatieve grootte van hun ionen en hun stoichiometrie (de twee belangrijkste kenmerken die de structuur bepalen) vergelijkbaar zijn.

Enkelementscellen van ionische verbindingen

Vele ionische verbindingen kristalliseren met kubische eenheidscellen, en we zullen deze verbindingen gebruiken om de algemene kenmerken van ionische structuren te beschrijven.

Wanneer een ionische verbinding is samengesteld uit kationen en anionen van gelijke grootte in een 1:1 verhouding, vormt zij gewoonlijk een eenvoudige kubische structuur. Cesiumchloride, CsCl, (afgebeeld in figuur 14) is hier een voorbeeld van, waarbij Cs+ en Cl- stralen hebben van respectievelijk 174 pm en 181 pm. We kunnen dit zien als chloride-ionen die een eenvoudige kubische eenheidscel vormen, met een cesium-ion in het centrum; of als cesium-ionen die een eenheidscel vormen met een chloride-ion in het centrum; of als eenvoudige kubische eenheidscellen gevormd door Cs+-ionen die eenheidscellen gevormd door Cl-ionen overlappen. Cesiumionen en chloride-ionen raken elkaar langs de lichaamsdiagonalen van de eenheidscellen. Per eenheidscel is één cesiumion en één chloride-ion aanwezig, hetgeen de l:l stoichiometrie oplevert die de formule voor cesiumchloride voorschrijft. Merk op dat er geen roosterpunt in het midden van de cel is, en CsCl is geen BCC structuur omdat een cesiumion niet identiek is aan een chloride-ion.

Figuur 14. Ionische verbindingen met kationen en anionen van gelijke grootte, zoals CsCl, vormen gewoonlijk een eenvoudige kubische structuur. Zij kunnen worden beschreven door eenheidscellen met hetzij kationen op de hoeken, hetzij anionen op de hoeken.

We hebben gezegd dat de plaats van de roosterpunten arbitrair is. Dit wordt geïllustreerd door een alternatieve beschrijving van de CsCl-structuur waarin de roosterpunten zich in de centra van de cesiumionen bevinden. In deze beschrijving bevinden de cesiumionen zich op de roosterpunten op de hoeken van de cel, en het chloride-ion bevindt zich in het midden van de cel. De twee eenheidscellen zijn verschillend, maar zij beschrijven identieke structuren.

Wanneer een ionische verbinding is samengesteld uit een 1:1 verhouding van kationen en anionen die aanzienlijk in grootte verschillen, kristalliseert zij typisch met een FCC eenheidscel, zoals die in figuur 15 wordt getoond. Natriumchloride, NaCl, is hier een voorbeeld van, met Na+ en Cl- met stralen van respectievelijk 102 pm en 181 pm. We kunnen dit zien als een FCC cel met chloride-ionen, waarbij de natrium-ionen zich in de octahedrale gaten in het midden van de celranden en in het midden van de cel bevinden. De natrium- en chloride-ionen raken elkaar langs de celranden. De eenheidscel bevat vier natriumionen en vier chloride-ionen, wat de stoichiometrie 1:1 oplevert die vereist is voor de formule NaCl.

Figuur 15. Ionische verbindingen met anionen die veel groter zijn dan kationen, zoals NaCl, vormen meestal een FCC-structuur. Zij kunnen worden beschreven door FCC-eenheidscellen met kationen in de octahedrale gaten.

De kubische vorm van zinksulfide, zinkblende, kristalliseert ook in een FCC-eenheidscel, zoals geïllustreerd in figuur 16. Deze structuur bevat sulfide-ionen op de roosterpunten van een FCC-rooster. (De rangschikking van de sulfide-ionen is identiek aan de rangschikking van de chloride-ionen in natriumchloride). De straal van een zinkion is slechts ongeveer 40% van de straal van een sulfide-ion, dus deze kleine Zn2+ ionen bevinden zich in alternerende tetrahedrale gaten, dat wil zeggen, in de ene helft van de tetrahedrale gaten. Er zijn vier zinkionen en vier sulfide-ionen in de eenheidscel, waardoor de empirische formule ZnS.

Figuur 16. ZnS, zinksulfide (of zinkblende) vormt een FCC-eenheidscel met sulfide-ionen op de roosterpunten en veel kleinere zinkionen die de helft van de tetrahedrale gaten in de structuur bezetten.

Een calciumfluoride-eenheidscel, zoals die in figuur 17, is ook een FCC-eenheidscel, maar in dit geval bevinden de kationen zich op de roosterpunten; equivalente calciumionen bevinden zich op de roosterpunten van een FCC-rooster. Alle tetrahedral sites in de FCC array van calciumionen worden bezet door fluoride-ionen. Er zijn vier calciumionen en acht fluoride-ionen in een eenheidscel, wat een calcium:fluorverhouding geeft van l:2, zoals de chemische formule CaF2 vereist. Bij nadere bestudering van figuur 17 ziet men een eenvoudige kubische array van fluoride-ionen met calciumionen in de ene helft van de kubische gaten. De structuur kan niet worden beschreven in termen van een ruimtelijk rooster van punten op de fluoride-ionen omdat de fluoride-ionen niet allemaal een identieke omgeving hebben. De oriëntatie van de vier calciumionen rond de fluoride-ionen verschilt.

Figuur 17. Calciumfluoride, CaF2, vormt een FCC-eenheidscel met calciumionen (groen) in de roosterpunten en fluoride-ionen (rood) die alle tetrahedral sites tussen hen bezetten.

Berekening van ionenstralingen

Als we de randlengte van een eenheidscel van een ionische verbinding en de plaats van de ionen in de cel kennen, kunnen we ionenstralingen voor de ionen in de verbinding berekenen als we aannamen maken over individuele ionenvormen en contacten.

Voorbeeld 5: Berekening van ionstraal

De randlengte van de eenheidscel van LiCl (NaCl-achtige structuur, FCC) is 0.514 nm of 5,14 Å. Aangenomen dat het lithiumion klein genoeg is zodat de chloride-ionen met elkaar in contact komen, zoals in figuur 15, bereken dan de ionstraal voor het chloride-ion.

Noot: De lengte-eenheid angstrom, Å, wordt vaak gebruikt om afmetingen op atomaire schaal weer te geven en is gelijk aan 10-10 m.

Toon oplossing

Op het vlak van een LiCl-eenheidscel komen chloride-ionen met elkaar in contact over de diagonaal van het vlak:

Tekening van een rechthoekige driehoek op het vlak van de eenheidscel leert ons dat de lengte van de diagonaal gelijk is aan vier chloride-stralen (een straal van elk hoekchloride en een diameter – die gelijk is aan twee stralen – van het chloride-ion in het midden van het vlak), dus d = 4r. Uit de stelling van Pythagoras volgt:

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}^{2}

waaruit volgt:

(0,514 text{ nm}}rechts)^{2}+(0.514\text{ nm}\right)^{2}={\left(4r\right)}^{2}=16{r}^{2}

Solving this gives:

r=\sqrt{\dfrac{{(0.514\text{nm})}^{2}+{(0.514\text{nm})}^{2}}{16}}=\text{0.182 nm} (1,82 Å) voor een Cl-straal

Check Your Learning

De randlengte van de eenheidscel van KCl (NaCl-achtige structuur, FCC) bedraagt 6,28 Å. Bereken, uitgaande van anion-kation contact langs de celrand, de straal van het kaliumion. De straal van het chloride-ion is 1,82 Å.

Toon oplossing

De straal van het kalium-ion is 1,33 Å.

Het is belangrijk te beseffen dat waarden voor ionische stralen berekend op basis van de randlengten van eenheidscellen afhankelijk zijn van talrijke aannames, zoals een perfecte bolvorm voor ionen, die op zijn best benaderingen zijn. Dergelijke berekende waarden zijn dus zelf benaderingen en vergelijkingen kunnen niet te ver worden doorgedreven. Niettemin is deze methode nuttig gebleken voor de berekening van ionische stralen uit experimentele metingen zoals röntgenkristallografische bepalingen.

Röntgenkristallografie

De grootte van de eenheidscel en de rangschikking van atomen in een kristal kunnen worden bepaald uit metingen van de diffractie van röntgenstralen door het kristal, röntgenkristallografie genoemd. Diffractie is de verandering van de reisrichting van een elektromagnetische golf wanneer deze een fysische barrière ontmoet waarvan de afmetingen vergelijkbaar zijn met die van de golflengte van het licht. Röntgenstraling is elektromagnetische straling met golflengten die ongeveer even lang zijn als de afstand tussen naburige atomen in kristallen (in de orde van enkele Å).

Wanneer een bundel monochromatische röntgenstralen een kristal treft, worden de stralen in alle richtingen verstrooid door de atomen in het kristal. Wanneer verstrooide golven die in dezelfde richting gaan, elkaar tegenkomen, ondergaan zij interferentie, een proces waarbij de golven combineren en een vergroting of verkleining van de amplitude (intensiteit) veroorzaken, afhankelijk van de mate waarin de maxima van de gecombineerde golven van elkaar gescheiden zijn (zie figuur 18).

Figuur 18. Lichtgolven die dezelfde ruimte innemen ondervinden interferentie, en combineren tot golven met een grotere (a) of kleinere (b) intensiteit, afhankelijk van de scheiding van hun maxima en minima.

Wanneer röntgenstralen met een bepaalde golflengte, λ, worden verstrooid door atomen in aangrenzende kristalvlakken die op een afstand, d, van elkaar zijn verwijderd, kunnen zij constructieve interferentie ondergaan wanneer het verschil tussen de afstanden die door de twee golven vóór hun combinatie zijn afgelegd een gehele factor, n, van de golflengte is. Aan deze voorwaarde is voldaan wanneer de hoek van de verstrooide bundel, θ, met de golflengte en de interatomaire afstand is verbonden door de vergelijking:

n{\lambda }=2d{sin}theta

Deze relatie staat bekend als de Bragg-vergelijking, ter ere van W. H. Bragg, de Engelse natuurkundige die dit verschijnsel voor het eerst heeft verklaard. Figuur 19 illustreert twee voorbeelden van verstrooide golven van dezelfde twee kristalvlakken. De linker figuur toont golven die worden gebroken onder de Bragghoek, hetgeen constructieve interferentie oplevert, terwijl de rechter figuur diffractie toont onder een andere hoek die niet aan de Bragg-voorwaarde voldoet, hetgeen destructieve interferentie oplevert.

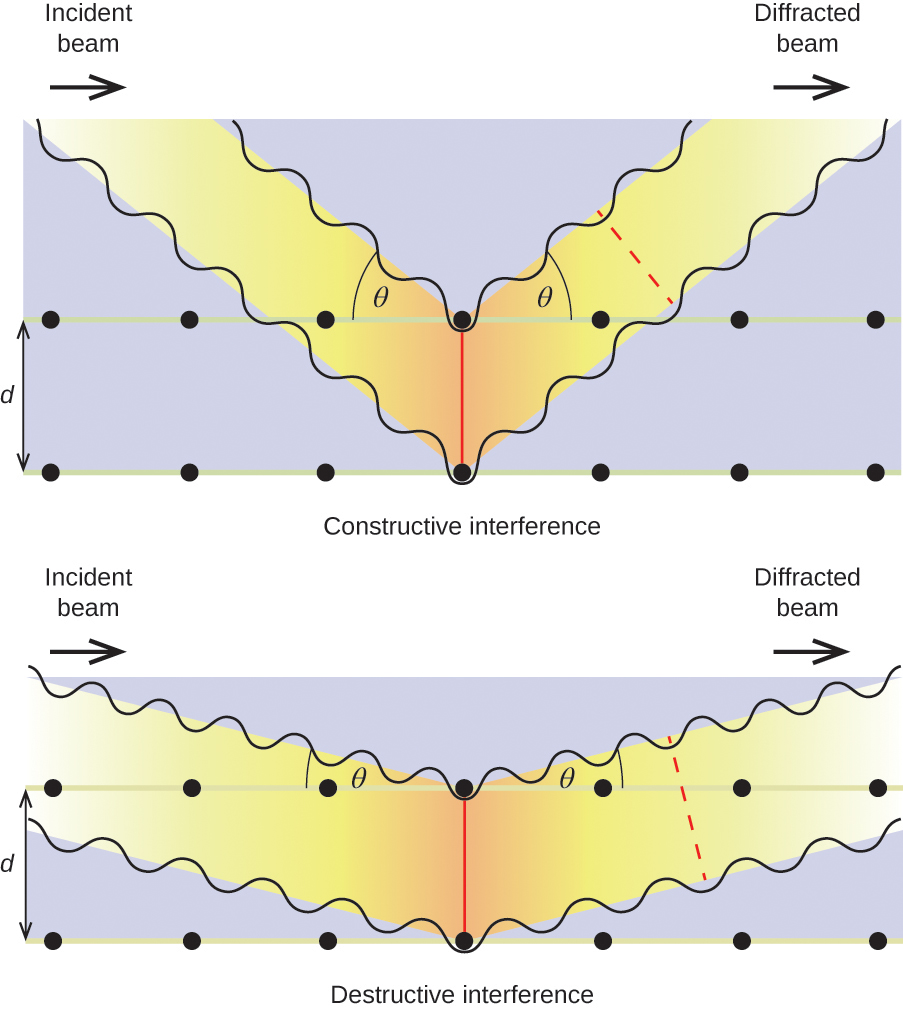
Figuur 19. De diffractie van röntgenstralen die door de atomen in een kristal worden verstrooid, maakt het mogelijk de afstand tussen de atomen te bepalen. Het bovenste beeld toont de constructieve interferentie tussen twee verstrooide golven en een resulterende verstrooide golf van hoge intensiteit. De onderste afbeelding toont de destructieve interferentie en een golf met een lage intensiteit die wordt afgeleid.

Een röntgendiffractometer, zoals die in figuur 20, kan worden gebruikt om de hoeken te meten waaronder röntgenstraling wordt gebroken bij interactie met een kristal zoals hierboven beschreven. Uit dergelijke metingen kan de Bragg-vergelijking worden gebruikt om afstanden tussen atomen te berekenen, zoals in het volgende voorbeeld wordt gedemonstreerd.

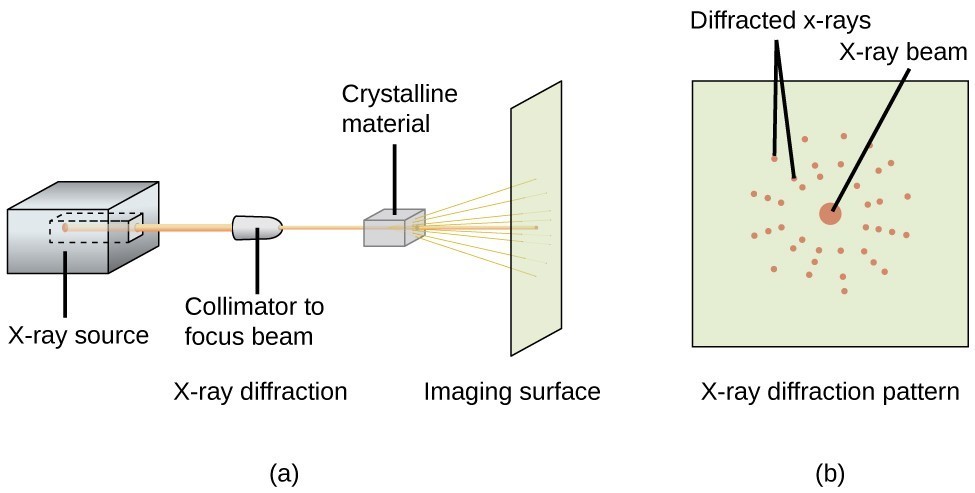
Figuur 20. In een diffractometer (a) treft een bundel röntgenstralen een kristallijn materiaal, waarbij een röntgendiffractiepatroon (b) wordt geproduceerd dat kan worden geanalyseerd om de kristalstructuur te bepalen.

Hier kunt u het transcript van “Celebrating Crystallography – An animated adventure” bekijken (opent in een nieuw venster).

Voorbeeld 6: Met behulp van de Bragg-vergelijking

In een diffractometer werd met röntgenstraling met een golflengte van 0,1315 nm een diffractiepatroon voor koper gemaakt. De eerste-ordediffractie (n = 1) vond plaats onder een hoek θ = 25,25°. Bepaal de afstand tussen de diffracterende vlakken in koper.

Toon oplossing

De afstand tussen de vlakken wordt gevonden door de Bragg-vergelijking, nλ = 2d sin θ, op te lossen voor d.

Dit levert op: d=:frac{n}lambda}{2:sin}frac{1}(0.1315 nm}rechts)}{2\sinlinks(25,25^{circ}rechts)}=0,154 nm}

Check Your Learning

Een kristal met een afstand tussen de vlakken gelijk aan 0,394 nm diffundeert röntgenstraling met een golflengte van 0,147 nm. Wat is de hoek voor de eerste-ordediffractie?

Oplossing tonen

10,8°

Portret van een chemicus: X-ray Crystallographer Rosalind Franklin

Figuur 21. Deze illustratie toont een röntgendiffractiebeeld dat lijkt op het beeld dat Franklin in haar onderzoek vond. (credit: National Institutes of Health)

De ontdekking van de structuur van DNA in 1953 door Francis Crick en James Watson is een van de grote prestaties in de geschiedenis van de wetenschap. Zij kregen de Nobelprijs voor fysiologie of geneeskunde in 1962, samen met Maurice Wilkins, die experimenteel bewijs leverde voor de structuur van DNA. De Britse chemicus Rosalind Franklin leverde een onschatbare bijdrage aan deze monumentale prestatie door haar werk bij het meten van röntgendiffractiebeelden van DNA. In het begin van haar carrière bleek Franklins onderzoek naar de structuur van kolen van nut te zijn voor de Britse oorlogsinspanningen. Nadat ze begin jaren 1950 haar aandacht had verlegd naar biologische systemen, ontdekten Franklin en doctoraatsstudent Raymond Gosling dat DNA uit twee vormen bestaat: een lange, dunne vezel die gevormd wordt wanneer hij nat is (type “B”) en een korte, brede vezel die gevormd wordt wanneer hij gedroogd is (type “A”). Haar röntgendiffractiebeelden van DNA (Figuur 21) leverden de cruciale informatie die Watson en Crick in staat stelden te bevestigen dat DNA een dubbele helix vormt, en de details van de grootte en structuur ervan vast te stellen.

Franklin verrichtte ook baanbrekend onderzoek naar virussen en het RNA dat hun genetische informatie bevat, en bracht nieuwe informatie aan het licht die de hoeveelheid kennis op dit gebied radicaal veranderde. Nadat ze eierstokkanker had gekregen, bleef Franklin doorwerken tot haar dood in 1958 op 37-jarige leeftijd. Een van de vele postume erkenningen van haar werk was dat de Chicago Medical School of Finch University of Health Sciences in 2004 haar naam veranderde in de Rosalind Franklin University of Medicine and Science, en een afbeelding van haar beroemde röntgendiffractie-afbeelding van DNA aannam als het officiële universiteitslogo.

Key Concepts and Summary

De structuren van kristallijne metalen en eenvoudige ionische verbindingen kunnen worden beschreven in termen van pakking van bollen. Metaalatomen kunnen zich oppakken in hexagonale dicht opeen gepakte structuren, kubische dicht opeen gepakte structuren, lichaamsgecentreerde structuren, en eenvoudige kubische structuren. De anionen in eenvoudige ionische structuren nemen gewoonlijk één van deze structuren aan, en de kationen bezetten de ruimten die tussen de anionen overblijven. Kleine kationen bezetten gewoonlijk tetrahedrale gaten in een dicht opeen gepakte rij anionen. Grotere kationen bezetten meestal octahedrale gaten. Nog grotere kationen kunnen kubische gaten bezetten in een eenvoudige kubische opstelling van anionen. De structuur van een vaste stof kan worden beschreven door de grootte en vorm van een eenheidscel en de inhoud van de cel aan te geven. Het type structuur en de afmetingen van de eenheidscel kunnen worden bepaald door röntgendiffractiemetingen.

Key Equations

• n{lambda }=2d{sin}theta

Try It

1. Beschrijf de kristalstructuur van ijzer, dat kristalliseert met twee equivalente metaalatomen in een kubische eenheidscel.
2. Beschrijf de kristalstructuur van Pt, dat met vier equivalente metaalatomen in een kubische eenheidscel kristalliseert.
3. Wat is het coördinatiegetal van een chroomatoom in de lichaamsgecentreerde kubische structuur van chroom?
4. Wat is het coördinatiegetal van een aluminiumatoom in de gezichtsgecentreerde kubische structuur van aluminium?
5. Kobaltmetaal kristalliseert in een hexagonale dicht opeen gepakte structuur. Wat is het coördinatiegetal van een kobaltatoom?
6. Nikkelmetaal kristalliseert in een kubische dichtst gepakte structuur. Wat is het coördinatiegetal van een nikkelatoom?
7. Wolfraam kristalliseert in een lichaam-gecentreerde kubische eenheidscel met een randlengte van 3,165 Å.
   1. Wat is de atomaire straal van wolfraam in deze structuur?
   2. Bereken de dichtheid van wolfraam.
8. Platina (atomaire straal = 1,38 Å) kristalliseert in een kubische dicht opeengepakte structuur. Bereken de randlengte van de face-centered cubic eenheidscel en de dichtheid van platina.
9. Barium kristalliseert in een body-centered cubic eenheidscel met een randlengte van 5.025 Å
   1. Wat is de atomaire straal van barium in deze structuur?
   2. Bereken de dichtheid van barium.
10. Aluminium (atomaire straal = 1,43 Å) kristalliseert in een kubische dicht opeengepakte structuur. Bereken de randlengte van de face-centered cubic eenheidscel en de dichtheid van aluminium.
11. De dichtheid van aluminium is 2,7 g/cm3; die van silicium is 2,3 g/cm3. Leg uit waarom Si de lagere dichtheid heeft, ook al heeft het zwaardere atomen.
12. De vrije ruimte in een metaal kan worden gevonden door het volume van de atomen in een eenheidscel af te trekken van het volume van de cel. Bereken het percentage vrije ruimte in elk van de drie kubische roosters als alle atomen in elk even groot zijn en hun naaste buren raken. Welke van deze structuren vertegenwoordigt de meest efficiënte verpakking? Dat wil zeggen, welke pakt in met de minste ongebruikte ruimte?
13. Cadmiumsulfide, soms door kunstenaars gebruikt als geel pigment, kristalliseert met cadmium, dat de helft van de tetrahedrale gaten inneemt in een dicht opeengepakte rij sulfide-ionen. Wat is de formule van cadmiumsulfide? Leg uw antwoord uit.
14. Een verbinding van cadmium, tin en fosfor wordt gebruikt bij de fabricage van sommige halfgeleiders. Het kristalliseert met cadmium bezet een vierde van de tetrahedrale gaten en tin bezet een vierde van de tetrahedrale gaten in een dicht opeengepakte array van fosfide-ionen. Wat is de formule van de verbinding? Leg uw antwoord uit.
15. Wat is de formule van het magnetische kobaltoxide, dat wordt gebruikt in opnametapes en kristalliseert met kobaltatomen die een achtste van de tetrahedrale gaten en de helft van de octahedrale gaten in een dicht opeengepakte array van oxide-ionen bezetten?
16. Een verbinding die zink, aluminium en zwavel bevat, kristalliseert met een dicht opeengepakte array van sulfide-ionen. Zinkionen bevinden zich in een achtste van de tetrahedrale gaten en aluminiumionen in de helft van de octahedrale gaten. Wat is de empirische formule van deze verbinding?
17. Een verbinding van thallium en jodium kristalliseert in een eenvoudige kubische array van jodide-ionen met thallium-ionen in alle kubische gaten. Wat is de formule van dit jodide? Leg uw antwoord uit.
18. Welk van de volgende elementen reageert met zwavel om een vaste stof te vormen waarin de zwavelatomen een dicht opeen gepakte array vormen met alle octahedrale gaten bezet: Li, Na, Be, Ca, of Al?
19. Wat is het massapercentage titaan in rutiel, een mineraal dat titaan en zuurstof bevat, als de structuur kan worden beschreven als een dicht opeengepakte array van oxide-ionen met titaanionen in de helft van de octaëdervormige gaten? Wat is het oxidatiegetal van titaan?
20. Verklar waarom de chemisch gelijksoortige alkalimetaalchloriden NaCl en CsCl verschillende structuren hebben, terwijl de chemisch verschillende NaCl en MnS dezelfde structuur hebben.
21. Toen mineralen uit het gesmolten magma werden gevormd, bezetten verschillende ionen dezelfde cites in de kristallen. Lithium komt vaak samen met magnesium in mineralen voor, ondanks het verschil in lading van hun ionen. Geef een verklaring.
22. Rubidiumjodide kristalliseert met een kubische eenheidscel die jodide-ionen bevat op de hoeken en een rubidiumion in het centrum. Wat is de formule van de verbinding?
23. Een van de verschillende mangaanoxiden kristalliseert met een kubische eenheidscel die mangaanionen bevat op de hoeken en in het centrum. De oxide-ionen bevinden zich in het midden van elke rand van de eenheidscel. Wat is de formule van de verbinding?
24. NaH kristalliseert met dezelfde kristalstructuur als NaCl. De randlengte van de kubische eenheidscel van NaH is 4,880 Å.
    1. Bereken de ionstraal van H-. (De ionstraal van Li+ is 0,0,95 Å.)
    2. Bereken de dichtheid van NaH.
25. Thallium(I)-jodide kristalliseert met dezelfde structuur als CsCl. De randlengte van de eenheidscel van TlI is 4,20 Å.
    1. Bereken de ionstraal van TI+. (De ionstraal van I- is 2,16 Å.)
    2. Bereken de dichtheid van TlI.
26. Een kubische eenheidscel bevat mangaanionen op de hoeken en fluoride-ionen in het midden van elke rand.
    1. Wat is de empirische formule van deze verbinding? Leg uw antwoord uit.
    2. Wat is het coördinatiegetal van het Mn3+ ion?
    3. Bereken de randlengte van de eenheidscel als de straal van een Mn3+ ion 0,65 A is.
    4. Bereken de dichtheid van de verbinding.
27. Wat is de afstand tussen kristalvlakken die röntgenstraling met een golflengte van 1,541 nm bij een hoek θ van 15,55° diffunderen (eerste-orde-reflectie)?
28. Een diffractometer die röntgenstraling met een golflengte van 0,2287 nm gebruikt, produceert een eerste-orde-diffractiepiek bij een kristalhoek θ = 16,21°. Bepaal de afstand tussen de diffracterende vlakken in dit kristal.
29. Een metaal met een afstand tussen de vlakken gelijk aan 0,4164 nm diffracteert röntgenstraling met een golflengte van 0,2879 nm. Wat is de diffractiehoek voor de eerste-orde-diffractiepiek?
30. Goud kristalliseert in een face-centered cubic eenheidscel. De tweede-orde-reflectie (n = 2) van röntgenstraling voor de vlakken die de boven- en onderkant van de eenheidscellen vormen, ligt bij θ = 22,20°. De golflengte van de röntgenstraling is 1,54 Å. Wat is de dichtheid van metallisch goud?
31. Als een elektron in een aangeslagen molybdeenatoom van de L- naar de K-schil valt, wordt er een röntgenstraling uitgezonden. Deze röntgenstraling wordt onder een hoek van 7,75° afgebogen door vlakken met een onderlinge afstand van 2,64 Å. Wat is het energieverschil tussen de K-schil en de L-schil in molybdeen, uitgaande van een eerste-orde diffractie?

Toon geselecteerde oplossingen

1. De structuur van deze lage-temperatuur-vorm van ijzer (beneden 910 °C) is lichaam-gecentreerd kubisch. Er is een achtste atoom op elk van de acht hoeken van de kubus en een atoom in het centrum van de kubus.

3. Coördinatiegetal verwijst naar het aantal naaste buren. Een chroomatoom ligt in het centrum van een lichaamsgecentreerde kubus en heeft acht naaste buren (op de hoeken van de kubus): vier in een vlak boven en vier in een vlak onder. Het coördinatiegetal is dus acht.

5. Hexagonale nauwe pakking gebeurt zodanig dat elk atoom 12 naaste buren heeft: 6 in zijn eigen laag en 3 in elke aangrenzende laag. Het coördinatiegetal is dus 12.

7. (a) In een lichaam-gecentreerde kubische eenheidscel zijn de metaalatomen in contact langs de binnendiagonaal van de kubus. De binnendiagonaal vormt een rechthoekige driehoek met de eenheidscelrand en de diagonaal van het vlak. Gebruik de stelling van Pythagoras om de lengte van de diagonaal, d, op het zijvlak van de kubus te bepalen in termen van de rand, e.

d2 = e2 + e2 = 2e2

d = \sqrt{2} e

De binnendiagonaal van de kubus is de lengte van vier atomaire stralen en kan opnieuw berekend worden met behulp van de stelling van Pythagoras en de diagonaal van het zijvlak en de rand.

begin{array}{rll}links(\text{diagonaal}rechts)^2&=&d^2+e^2 \\ &=&links(\sqrt{2} e}rechts)+e^2 \ &=& 2e^2+e^2 \ &=&3e^2 \text{diagonaal}&=&\sqrt{3}e=4r eind{array}

radius van wolfraam = \frac{text{diagonaal}}{4}=\frac{\sqrt{3}}{4}} links(3..165mathring{A}}rechts)=1.370mathring{A}};

(b) Gegeven de lichaamsgecentreerde kubische structuur, bevat elke eenheidscel twee atomen. Bereken met behulp van de eenheidscelrandlengte het eenheidscelvolume en het volume dat door elk atoom wordt ingenomen. Vermenigvuldig om het molaire volume te verkrijgen en deel de atoommassa door deze waarde om de dichtheid (e = randlengte) te verkrijgen:

V(cel) = e3 = (3,165 maal 10-8 cm)3 = 3,170 maal 10-23 cm3

V(atoom) = \frac{3,170 maal {10}^{-23}{10}^{cm}}^{3}}{2 atomen}}=1.585 maal {10}^{-23}{\text{cm}}^{3}{\text{atom}}^{-1}

V(mol) = 1,585 maal 10-23 cm3/atoom maal 6,022 maal 1023 atomen/mol

= 9.546 cm3/mol

dichtheid = \frac{183,85{g mol}}^{-1}}{9,546{text{cm}}^{3}{text{mol}}^{-1}} = 19,26 g/cm

9. (a) In een kubusgecentreerde lichaamseenheidscel zijn de metaalatomen in contact langs de diagonaal van de kubus. De diagonaal van de kubus vormt een rechthoekige driehoek met de eenheidscelrand en de diagonaal van een zijvlak. Gebruik de stelling van Pythagoras om de lengte van de diagonaal, d, op het zijvlak van de kubus te bepalen in termen van e.

d2 = e2 + e2 = 2e2

d = \sqrt{2} e

De diagonaal van de kubus is de lengte van vier atomaire stralen en kan berekend worden door opnieuw de stelling van Pythagoras te gebruiken:

(diagonaal)2 = (4r)2 = (2e)2 + e2 = 16r2 = 3e2

diagonaal = 4r = \sqrt{3\text{e}}

r = \frac{\sqrt{3}}{4}\text{e}= \frac{\sqrt{3}}{4} (5,025 Å) = 2,176 Å;

(b) Gegeven een lichaam-gecentreerde kubische structuur, bevat elke eenheidscel twee atomen. Gebruik de lengte van de eenheidscelrand om het volume van de eenheidscel te berekenen en het volume dat elk atoom inneemt. Vermenigvuldig om het molaire volume te verkrijgen en deel het gram atoomgewicht door deze waarde om de dichtheid (e = randlengte) te verkrijgen:

V (cel) = e3 = (5,025 \times 10-8 cm)3 = 1,26884 \times 10-22 cm3

V (atoom) = 1.26884 maal \frac{10}^{-22}{\text{cm}}^{3}{\text{atom}}^{2 atomen}} = 6,3442 maal 10-23 cm3

V (mol) = 6.3442 maal 10-23 cm3 maal 6,022 maal 1023 atomen/mol = 38,205 cm3

d(Ba) = \frac{137,33 g}{38,204 cm}^{3} = 3,595 g/cm3

11. Uit de kristalstructuur van Si blijkt dat het minder dicht opeengepakt is (coördinatiegetal 4) in de vaste stof dan Al (coördinatiegetal 12).

13. In een dicht opeengepakte matrix zijn er voor elk anion twee tetrahedrale gaten. Als slechts de helft van de tetrahedral gaten bezet zijn, zijn de aantallen anionen en kationen gelijk. De formule voor cadmiumsulfide is CdS.

15. In een dicht opeen gepakte rij van oxide-ionen zijn er voor elk oxide-ion één octahedraal gat en twee tetrahedrale gaten. Als de helft van de octahedrale gaten gevuld is, is er één Co-ion voor elke twee oxide-ionen. Als een achtste van de tetrahedral gaten is gevuld, is er een Co-ion voor elke vier oxide-ionen. Voor elke vier oxide-ionen zijn er twee Co-ionen in octahedrale gaten en één Co in een tetrahedraal gat; de formule is dus Co3O4.

17. In een eenvoudige kubische matrix kan slechts één kubisch gat worden bezet door een kation voor elk anion in de matrix. De verhouding van thallium tot jodide moet 1:1 zijn; daarom is de formule voor thallium TlI.

19. De verhouding van octahedrale gaten tot zuurstofanionen is 1:1 in een “closest-packed array”. Slechts de helft van de octaërale gaten is bezet. De verhouding titaan/zuurstof is dus 1:2 en de formule is TiO2. Het massapercentage Ti in de structuur is:

percent Ti = \frac{47,90}{47,90+{2(15,9994)}} maal \text{100%}={59,95%}

Het oxidatiegetal van titaan is +4 omdat er voor elk Ti ion twee O2- ionen zijn.

21. Beide ionen liggen dicht bij elkaar in grootte: Mg, 0,65; Li, 0,60. Door deze overeenkomst kunnen de twee vrij gemakkelijk worden uitgewisseld. Het verschil in lading wordt in het algemeen gecompenseerd door de verwisseling van Si4+ voor Al3+.

23. Het totale aantal Mn-ionen wordt bepaald door de bijdragen van de hoeken en het centrum bij elkaar op te tellen. Mn (hoeken): 8 maal \frac{1}{8}; Mn (centrum) = 1. Totale Mn bijdrage aan de eenheidscel = 2.

Voor O zijn er in totaal 12 randen in de kubus en elk ion in de rand draagt eenvierde bij aan de eenheidscel. Er zijn dus 12 maal 1 = 3 O atomen. De verhouding is Mn:O = 2:3, en de formule is Mn2O3.

27. De Bragg-vergelijking luidt: nλ = 2d sin θ

waarbij d de afstand tussen de vlakken is.

d = \frac{n{\lambda }}{2 sin}\theta }=\frac{1(1.541 A}{2 sin15.55^{\circ}}=:frac{1.541 sin{\text{A}}}{2(0.2681)} = 2.874 Å

29. \θ = sin-1(0,3457) = 20,2°

31. Gebruik de Bragg-vergelijking, waarin n = 1,

λ = 2dsinθ =2(2,64 Å)sin 7,75 = 0,712 Å

Dan is E={hc}{\lambda}={(6.626 maal {10}^{-34}\text{J s})(2,998 maal {10}^{8}{text{m s}^{-1})}{0,712 maal {10}^{-10}\text{m}} =2,79 maal {10}^{-15}\text{J}=1.74 maal {10}^{4}}

Glossary

lichaamsgecentreerde kubus (BCC) vaste stof: kristallijne structuur met een kubische eenheidscel met roosterpunten op de hoeken en in het midden van de cel

lichaamsgecentreerde kubische eenheidscel: eenvoudigste zich herhalende eenheid van een lichaamsgecentreerd kubisch kristal; het is een kubus met roosterpunten op elke hoek en in het midden van de kubus

Bragg-vergelijking: vergelijking die betrekking heeft op de hoeken waaronder röntgenstraling door de atomen in een kristal wordt gebroken

coordinatiegetal: aantal atomen dat het dichtst bij een bepaald atoom in een kristal of bij het centrale metaalatoom in een complex ligt

cubic closest packing (CCP): kristalstructuur waarin vlakken van dicht opeengepakte atomen of ionen zijn gestapeld als een reeks van drie alternerende lagen met verschillende relatieve oriëntaties (ABC)

diffractie: Omleiding van elektromagnetische straling die optreedt wanneer deze een fysieke barrière van geschikte afmetingen tegenkomt

face-centered cubic (FCC) solid: kristallijne structuur bestaande uit een kubische eenheidscel met roosterpunten op de hoeken en in het midden van elk face

face-centered cubic eenheidscel: eenvoudigste zich herhalende eenheid van een face-centered cubic kristal; het is een kubus met roosterpunten op elke hoek en in het midden van elk vlak

hexagonal closest packing (HCP): kristallijne structuur waarin dicht opeengepakte lagen atomen of ionen zijn gestapeld als een reeks van twee afwisselende lagen met verschillende relatieve oriëntaties (AB)

gat: (ook, spleet) ruimte tussen atomen binnen een kristal

isomorf: dezelfde kristalstructuur bezittend

octahedraal gat: open ruimte in een kristal in het centrum van zes deeltjes die zich op de hoeken van een octaëder bevinden

eenvoudige kubische eenheidscel: (ook, primitieve kubische eenheidscel) eenheidscel in de eenvoudige kubische structuur

eenvoudige kubische structuur: kristalstructuur met een kubische eenheidscel met alleen op de hoeken roosterpunten

ruimte rooster: alle punten binnen een kristal die identieke omgevingen hebben

tetrahedraal gat: tetrahedrale ruimte gevormd door vier atomen of ionen in een kristal

eenheidscel: kleinste deel van een ruimterooster dat in drie dimensies wordt herhaald om het gehele rooster te vormen

röntgenkristallografie: experimentele techniek voor het bepalen van afstanden tussen atomen in een kristal door het meten van de hoeken waaronder röntgenstralen worden gebroken wanneer ze door het kristal gaan