Wat heb je aan karaktertabellen?
Op dit punt is een goede vraag: wat is het nut van het leren over karaktertabellen? Het eenvoudige antwoord is dat de symmetrie en de bijbehorende karaktertabel van een molecuul kunnen worden gebruikt om vele aspecten van chemisch significante spectroscopieën en bindingen te interpreteren en te voorspellen. We zullen dit nu illustreren door ons te richten op de vibratiemodes van een molecuul.
In het laboratorium kunnen we nuttige experimentele gegevens verzamelen met behulp van infrarood- (IR) en Raman-spectroscopie. Deze gegevens kunnen worden vergeleken met het aantal actieve IR- en/of Raman-banden dat wordt voorspeld op grond van de toepassing van de groepentheorie en de juiste karaktertabel. De wiskunde (groepentheorie en matrixalgebra) achter deze behandeling dient als een solide theoretische basis. De hieronder beschreven manipulaties werken omdat alle symmetriebewerkingen van een molecuul een wiskundige groep vormen en aan de regels van de groep gehoorzamen. Zoals eerder opgemerkt hoeven we dit gebied van de wiskunde niet te beheersen om goed gebruik te kunnen maken van karaktertabellen.
Vrijheidsgraden en trillingen in Moleculen
Hier zullen we in eerste instantie de vrijheidsgraden voor een eenvoudig molecuul (water) bespreken. We zullen heel snel zien waarom het heel nuttig is om symmetrie te gebruiken bij het onderzoek van grotere moleculen.
Voor een molecuul met “N” atomen zijn er 3N vrijheidsgraden (vergeet niet dat we leven in een 3-dimensionale wereld van x, y, z coördinaten). Voor een niet-lineair molecuul kunnen 3 vrijheidsgraden worden toegekend aan translaties – beweging van een lichaam in zijn geheel (Tx, Ty, Tz) en 3 aan rotaties (Rx, Ry, Rz). De overige bewegingen van de atomen zijn verplaatsingen van de atomen ten opzichte van hun gemiddelde posities – het zwaartepunt verandert niet. Deze fundamentele trillingen worden “normale modi” genoemd. Een niet-lineair molecuul heeft dus 3N-6 normale modi. Voor water is het aantal normale toestanden 3 (3 x 3 – 6 = 3). Voor lineaire moleculen zijn er 3N-5 normale toestanden.
Voor water, dat natuurlijk intensief is bestudeerd, weten we dat de 3 trillingen als volgt zijn.
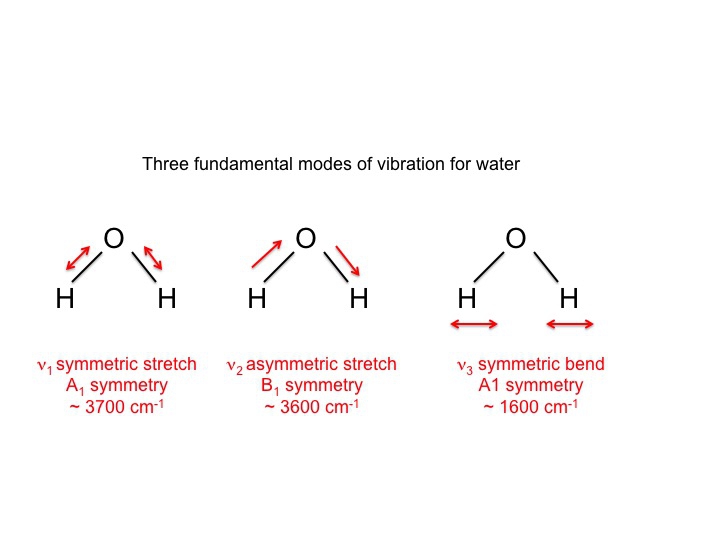
De symbolen die worden gebruikt om deze toestanden te beschrijven (A1, B1) zijn dezelfde Mulliken-symbolen die we zijn tegengekomen bij de bespreking van de karaktertabellen. Met andere woorden, de trillingen, die moleculaire eigenschappen zijn, kunnen worden beschreven door symmetriesoorten of onherleidbare representaties. In feite worden in veel literatuur over vibratiespectroscopie deze symbolen gebruikt als een stenografische manier om informatie door te geven.
Het zou vrij duidelijk moeten zijn dat het aantal trillingen snel toeneemt met zelfs maar een bescheiden toename van het aantal atomen in het molecuul. Het bepalen van de soorten trillingen door inspectie (zoals we deden voor water) wordt nu veel moeilijker. Neem bijvoorbeeld de volgende verbindingen:
H2O 3 atomen 3 trillingen
PH3 4 atomen 6 trillingen
CO22- 4 atomen 6 trillingen
XeF4 5 atomen 9 trillingen
B2H6 8 atomen 18 trillingen
Voor diboraan (B2H6) dat D2h symmetrie heeft, zou het een ontmoedigende taak zijn om de aard en de symmetriesoort van alle 18 trillingen door inspectie te achterhalen. Echter, gewapend met de karaktertabel voor D2h en kennis van symmetrie-eigenschappen is de taak van het bepalen van de symmetriesoort van alle trillingen rechttoe rechtaan.
Voor het geval van water zouden we de karaktertabel (C2v) kunnen presenteren met de 3 trillingen (ν1, v2, v3) opgesomd in de kolom van moleculaire eigenschappen, zoals hieronder getoond. (ν = Grieks symbool “nu”)

In het algemeen is deze aanpak echter onpraktisch. Neem bijvoorbeeld pyridine (C5H5N). De puntgroep is ook C2v, maar het molecuul heeft 11 atomen. Het aantal fundamentele trillingsmodes is 27 ( 3 x 11 – 6 = 27).
In dit geval zouden we een C2v-tekencodetabel moeten opstellen met de symmetrieën van alle 27 trillingen. Om deze reden worden trillingen normaliter niet in karaktertabellen opgenomen. In plaats daarvan is het aan de gebruiker (u) om het aantal en het type trillingen (zoals gedefinieerd door hun symmetrie-soort) te bepalen voor alle moleculen die men tegenkomt. Hoe we dit doen wordt hieronder beschreven.
Reducibele Representaties
Zoals eerder opgemerkt is een van de belangrijke eigenschappen van karaktertabellen dat de symmetrie operaties leden zijn van een wiskundige groep en dat er belangrijke relaties tussen hen bestaan. In het algemeen kan hetzelfde worden gezegd over de symmetriesoorten of irreducibele representaties van de moleculaire eigenschappen. De producten van het combineren van de tekens van onherleidbare representaties, hetzij door vermenigvuldiging, hetzij door optelling/aftrekking, gehoorzamen ook aan de regels van de groep. De nieuwe representaties zijn niet langer de eenvoudigst mogelijke en worden “herleidbare representaties” genoemd, omdat zij tot hun samenstellende delen kunnen worden “herleid”.
Bij voorbeeld, voor water kunnen de symmetrieën van de translaties (Tx, Ty, Tz) rechtstreeks uit de C2v karaktertabel worden afgeleid. Het zijn A1, B1, en B2. We kunnen alle drie deze vrijheidsgraden voorstellen door een voorstelling ΓT en we kunnen de uitdrukking hieronder schrijven. (Γ = Griekse hoofdletter “gamma”).
ΓT = A1 + B1 + B2
We weten dat A1, B1 en B2 slechts de stenografische notaties zijn voor de symmetriesoorten (onherleidbare representaties). We kunnen dus eenvoudig de tekens van ΓT opschrijven door de afzonderlijke tekens voor A1, B1 en B2 uit de C2v-karaktertabel bij elkaar op te tellen.
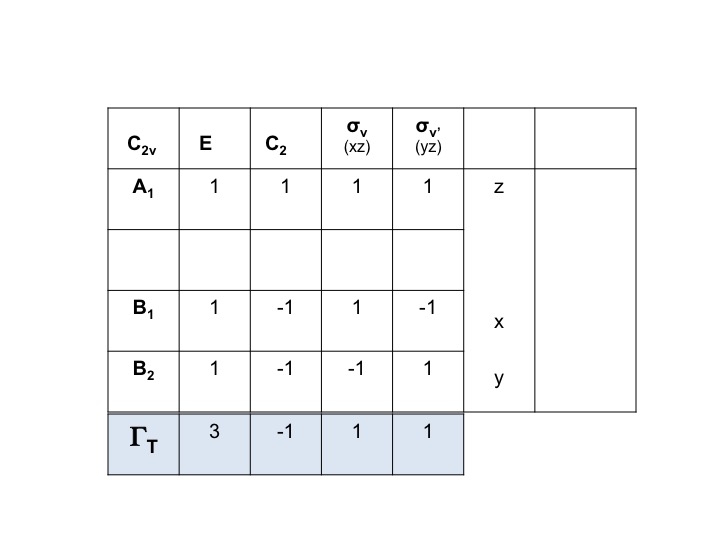
Tus ΓT = 3 -1 1 1.
Dit is een geldige herleidbare voorstelling en een lid van de C2v groep.
Op vergelijkbare wijze kunnen we de herleidbare voorstelling opschrijven voor alle drie de rotaties en alle trillingen.
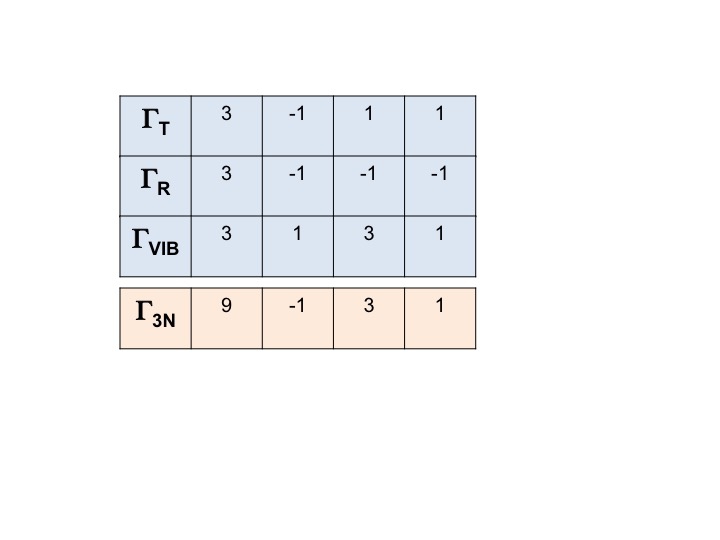
De voorstelling voor ALLE vrijheidsgraden voor het molecuul (3N) kan worden geschreven als
Γ3N = ΓT + ΓR + ΓVIB
en de herleidbare voorstelling ervoor wordt verkregen door eenvoudig de tekens voor ΓT, ΓR en ΓVIB bij elkaar op te tellen.
Γ3N = 9 -1 3 1
Noteer dit – het komt later nog aan de orde!
Hoewel de verzameling karakters 9 -1 3 1 een geldig lid is van de C2v groep, is het niet bijzonder nuttig bij de bespreking van moleculaire eigenschappen. Wat echt nodig is, is de taal van de steno symmetrie soorten (Mulliken symbolen, A1, B1 enz.). Met andere woorden, we willen Γ3N uitdrukken in termen van A1, B1 enz. Uit de hierboven behandelde informatie kan gemakkelijk door inspectie worden aangetoond dat:
Γ3N = 3A1 +A2 + 3B1 +2B2
Het goede nieuws is dat we deze taak voor andere, complexere moleculen niet door inspectie hoeven uit te voeren omdat:
1. We kunnen gemakkelijk Γ3N genereren als een herleidbare voorstelling voor een molecuul (als we zijn puntgroepsymmetrie kennen).
2. We kunnen de Γ3N herleidbare voorstelling gemakkelijk omzetten in de som van zijn symmetriesoorten (Mulliken-symbolen) met behulp van een “eenvoudige” formule die bekend staat als de reductieformule.
Algemene methode om Γ3N te verkrijgen
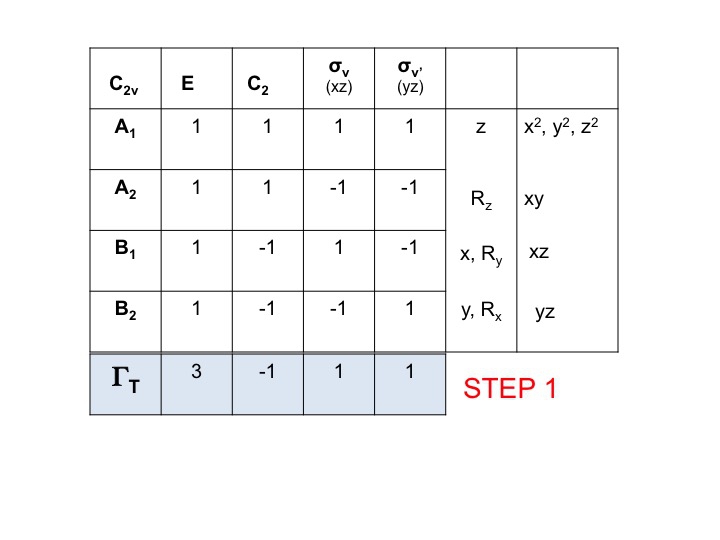
Stap 1
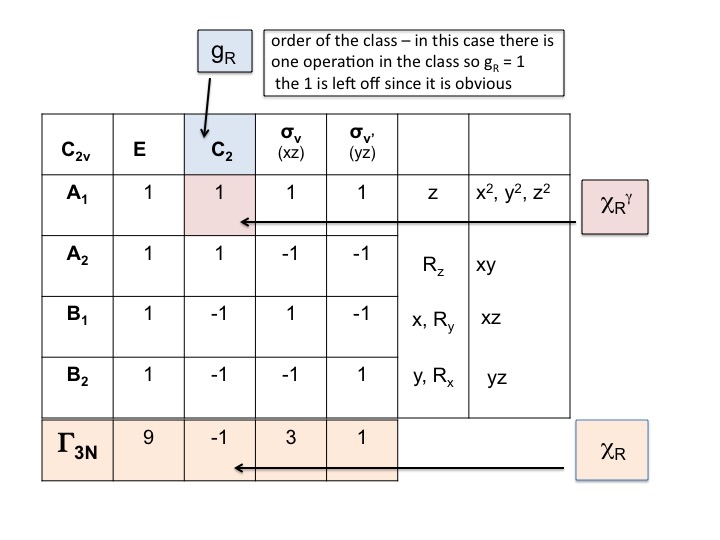
Neem de karaktertabel voor het molecuul en voeg onderaan een rij toe. In deze rij wordt de herleidbare voorstelling voor ΓT (of Γxyz) gegenereerd zoals we hierboven hebben gedaan, eenvoudigweg door voor elke bewerking de tekens toe te voegen die overeenkomen met de moleculaire eigenschappen voor x, y en z. Voor C2v hebben we al laten zien dat dit de tekens zijn die corresponderen met A1, B1 en B2.
Stap 2
Voeg onder ΓT nog een rij toe en noteer het aantal atomen dat bij elke symmetriebewerking NIET van plaats verandert. Dit is waar je je realiseert hoe nuttig een echte moleculaire modelreeks is. Hiervoor moet je ook weten waar de symmetrie-elementen zitten en hoe de symmetrie-bewerkingen het molecuul beïnvloeden. Natuurlijk weet je al hoe dit moet, omdat je Schönflies notatie hebt bestudeerd en weet hoe je de puntgroep van een molecuul moet toekennen. In de tekentabel staan ook alle symmetriebewerkingen per klasse op de bovenste rij.
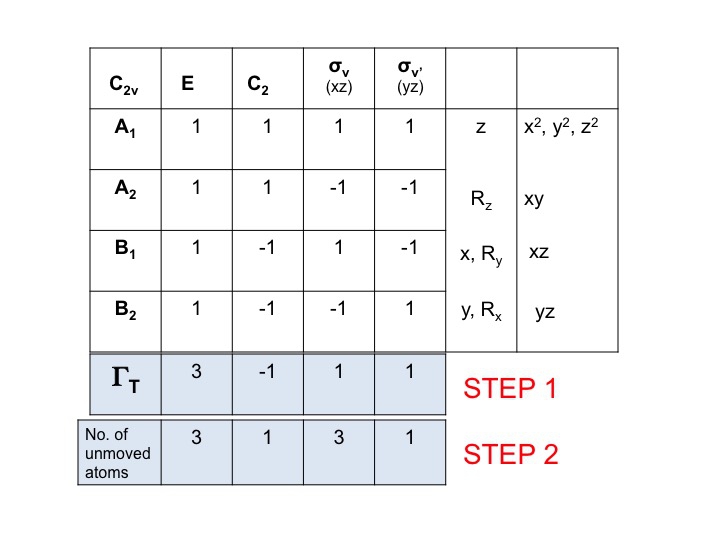
Zo zijn er voor water (3 atomen) onder E 3 onbewogen atomen, maar voor C2 bewegen beide H’s, maar omdat het O-atoom op de C2-as zit verandert het niet van plaats en dus noteren we 1 onder de C2-kolom. De nieuwe reeks getallen gegenereerd in stap 2 (3 1 3 1) is ook een herleidbare voorstelling in C2v en gehoorzaamt aan de regels van de groep.
Stap 3
In deze stap vermenigvuldigen we eenvoudig de tekens die in stap 1 en 2 zijn gegenereerd met elkaar. Het resultaat (derde rij) is de herleidbare voorstelling voor Γ3N (of ΓTOT). Zo eenvoudig is het.
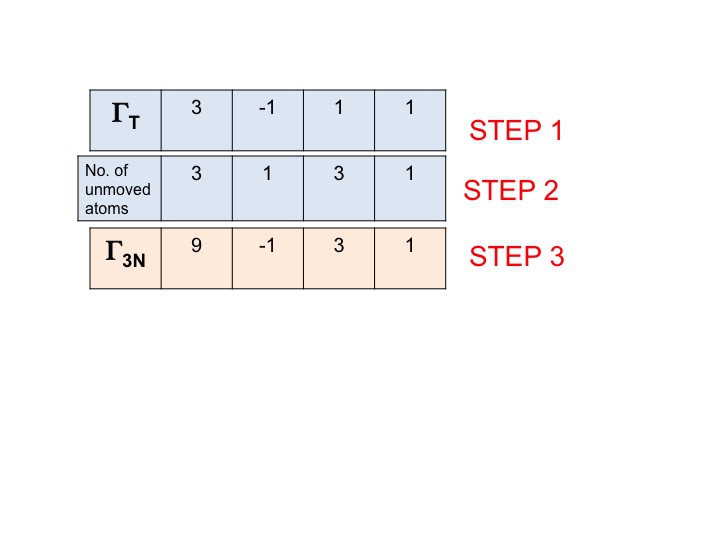
U zult opmerken dat de nieuwe herleidbare voorstelling (9 -1 1 3) identiek is aan de voorstelling voor Γ3N die we eerder door inspectie verkregen.
Reductie van de herleidbare representatie
Om ELKE herleidbare representatie om te zetten in de som van haar onherleidbare representaties (symmetriesoorten of Mulliken-symbolen) gebruiken we een reductieformule:

U kunt deze informatie gemakkelijk vinden in de karaktertabel:
Terug naar ons voorbeeld voor water: Puntgroep C2v, orde (g) = 4
De herleidbare representatie voor Γ3N = 9 -1 3 1
Het aantal keren dat A1 in deze representatie voorkomt is dus
aA1 = 1/4 { 1.1.9 + 1.1. (-1) + 1.1.3 +1.1.1} = 3
dus Γ3N bevat 3 A1 symmetrie species. De aantallen van de andere symmetriesoorten worden als volgt berekend:
aA2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1).3 + 1.(-1).1 } = 1 één A2 aanwezig
aB1 = 1/4 { 1.1.9 + 1.(-1).(-1) + 1.1.3 + 1.(-1).1} = 1. = 3 3 B1 aanwezig
aB2 = 1/4 {1.1.9 + 1.(-1)(-1) + 1.(-1).3 + 1.1.1} = 2 2 B2 aanwezig
We kunnen nu schrijven Γ3N = 3A1 + A2 + 3B1 + 2B2 (precies wat we kregen door “inspectie” hierboven. We kunnen nu de symmetriesoorten voor de translaties en rotaties aftrekken en dit geeft ons het aantal en de symmetriesoorten van de fundamentele trillingsmodes. ΓT en ΓR kunnen rechtstreeks uit de karaktertabel worden verkregen.
Γ3N = 3A1 + A2 + 3B1 + 2B2
ΓT = A1 + B1 + B2
ΓR = A2 + B1 + B2
ΓVIB = Γ3N – ΓT ΓT – ΓR = 2A1 +B1
Dus de drie normale trillingswijzen voor water hebben de symmetrieën A1, A1 en B1.
We hebben nu een algemene methode om alle fundamentele trillingsmodes van een molecuul te bepalen en deze uit te drukken in de stenotaal van de Mulliken-symbolen. Dit is een van de oefeningen waarop je in Examen 1 wordt getoetst. De beste manier om met deze methode vertrouwd te raken is zoveel mogelijk voorbeelden te oefenen als je kunt!
Volgende: Selectieregels