Un área de interés creciente para los científicos que exploran la importancia, el poder o la influencia entre entidades se llama Teoría de Grafos. Las raíces de la teoría de los grafos se remontan a 1736, cuando el matemático Carl Ehler presentó a Leonhard Euler el problema de los puentes de Konigsberg.
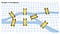
El problema de los puentes de Konigsberg se basa en la antigua ciudad alemana de Konigsberg, situada a ambos lados del río Pregel. En el centro, había dos grandes islas que estaban conectadas entre sí y con las orillas del río por siete puentes. Carl Ehler se obsesionó con encontrar una ruta para atravesar cada uno de los siete puentes sin pasar por ninguno de ellos más de una vez. Ehler se puso en contacto con Leonhard Euler, un matemático suizo. Euler confirmó la hipótesis de Ehler de que el problema no tenía solución, y la explicación de Euler dio lugar a un nuevo paradigma matemático llamado Geometría de la Posición.
El nuevo paradigma geométrico de Euler afirmaba que la ubicación de los puentes no importaba. El problema, en cambio, puede simplificarse convirtiendo cada puente en un punto (nodo) con líneas (aristas) para representar los enlaces entre ellos. Esta práctica de utilizar nodos y aristas se conoce ahora como Teoría de Grafos.
Puede leer más sobre el problema de los puentes de Konigsberg aquí.
Inicialmente, la Teoría de Grafos no tenía mucha utilidad en la resolución de problemas y no era muy apreciada por los matemáticos. Sin embargo, la moderna potencia de cálculo para procesar grandes permutaciones ha hecho que los principios de la Teoría de Grafos sean más prácticos. Este artículo le enseña a aplicar los principios de la Teoría de Grafos al análisis basado en Python.


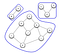
No todas las redes de un sistema de Grafos están interconectadas. Esta desconexión se produce cuando se forman los componentes. Como se muestra en el gráfico de abajo, un componente se forma sólo cuando cada nodo tiene un camino a otros nodos.
Teoría de grafos aplicada en Python
En Python, networkx se utiliza a menudo para la teoría de grafos aplicada también conocida como análisis de redes . El paquete tiene una funcionalidad útil para resumir rápidamente las características de un grafo. Usted puede revisar los pasos siguientes y seguir a lo largo de la creación de un gráfico y entender su composición.
Primero el código siguiente crea un objeto vacío gráfico P. Los siguientes pasos añaden nodos y describen las aristas.
Argumentos como <object>.nodes() o <object>.edges() son formas rápidas de ver todos los nodos y aristas del sistema de grafos.
print(P.nodes())print(P.edges())
Por último, nx.draw se utiliza para visualizar el grafo.
%matplotlib inline
import matplotlib.pyplot as plt
nx.draw(P, with_labels = True)
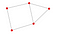
Ejercicios 1:
Ahora que se discuten los conceptos básicos de los grafos, los siguientes ejercicios son un buen método para practicar:
- ¿Cuántos nodos hay en el grafo anterior?
- ¿Cuántas aristas hay en el gráfico anterior?
- ¿Cuál es la geodésica de E y C?
- ¿Hay más de 1 componente en el gráfico?
Usando datos reales
El ejercicio siguiente utilizará datos de vuelos dentro de Estados Unidos en 2015. El conjunto de datos incluye los aeropuertos de origen y destino, además de los atributos que describen el vuelo, incluyendo el tiempo de vuelo y los retrasos (relacionados con el clima, la seguridad o la aerolínea).
Debido a que el conjunto de datos es grande, el ejercicio se concentrará en los vuelos que se originan en los aeropuertos del área de Los Ángeles (Los Ángeles (LAX), Burbank (BUR), el Condado de Orange (SNA) y el Condado de San Bernardino (ONT)). Además, nos centraremos en revisar los vuelos que se asemejan a mi horario de viaje de Deloitte – volando los domingos y regresando los jueves.
Dado que ya tenemos los datos de origen y destino, **** campos ORIGIN_AIRPORT y DESTINATION_AIRPORT servirán como campos de origen para los nodos y aristas – no hay necesidad de crear nodos o aristas como hicimos en el primer ejercicio. Una vez definidos los nodos, <object>.edges() proporcionará todas las relaciones de par entre ellos. Por último, nx.draw ayudará a producir un gráfico a las aristas.

FG.edges()

nx.draw(FG, with_labels = True)

En la salida anterior, los nodos están etiquetados con los códigos de los aeropuertos. Todas las aristas conducen a uno de los cuatro aeropuertos del área de Los Ángeles porque esos cuatro fueron los únicos seleccionados para este ejercicio. El aeropuerto internacional de Los Ángeles (LAX) es el más grande de los cuatro y el gráfico muestra claramente que muchas ciudades sólo son accesibles desde el LAX y no desde otros aeropuertos más pequeños. Esto pone de manifiesto la conectividad, o centralidad de grado, de LAX. En networkx, nx.algorithms.degree_centrality(<object>) ****se utiliza para encontrar la centralidad de cada nodo en el sistema de gráficos.
# Calculating the centrality of each of the airports
nx.algorithms.degree_centrality(FG)
Podemos ir más granular y utilizar un breve «bucle for» para producir aristas entre dos áreas de interés. Por ejemplo, el siguiente código se utiliza para encontrar todos los vuelos posibles desde el condado de San Bernardino (ONT) a Newark (EWR) ya sea el domingo o el jueves.
Entre las diversas opciones de vuelo entre el condado de San Bernardino y Newark, el nx.dijkstra_path se puede utilizar para encontrar la ruta euclidiana (o el camino más corto).
#Finding the dijkstra path
djk_path = nx.dijkstra_path(FG, source='ONT', target='EWR')
djk_path
Ejercicios 2:
- Producir el siguiente gráfico utilizando
nx.draw(). Nota: tu grafo puede no ser exactamente igual pero los caminos, aristas y nodos deben coincidir con el grafo de abajo. - Imprime todas las aristas.
- ¿Cuál es el camino más corto de L a F?

.