- Learning Outcomes
- 金属の構造
- 金属の単位胞
- 例1:金属の原子半径と密度の計算、その1
- Check Your Learning
- 例題2:金属の原子半径と密度の計算 その2
- その1
- その2
- Check Your Learning
- イオン結晶の構造
- 例3:四面体穴の占有率
- Check Your Learning
- 例4:イオン化合物の化学量論
- Check Your Learning
- イオン性化合物のユニットセル
- イオン半径の計算
- 例5:イオン半径の計算
- Check Your Learning
- X 線結晶学
- 例題6:ブラッグ式を使う
- Check Your Learning
- ある化学者の肖像: X線結晶学者ロザリンド・フランクリン
- Key Equations
- Try It
- Glossary
Learning Outcomes
- 結晶構造における原子とイオンの配列を説明できる
- 単位セルの寸法を用いてイオン半径を計算できる
- X-線の使用について説明する。結晶構造を決定するための回折測定
自然界に存在する固体および人工の固体の90%以上は結晶性である。 ほとんどの固体は、粒子が規則正しく配列された状態で形成される。なぜなら、粒子が最も効率的な方法でパックされると、粒子間の全体的な引力相互作用が最大になり、全分子間エネルギーが最小になるためである。 原子レベルでの規則正しい配列は、しばしば巨視的なレベルにも反映されます。 このモジュールでは、金属およびイオン性の結晶性固体の構造に関するいくつかの詳細を調べ、これらの構造がどのように実験的に決定されるかを学びます。
金属の構造
結晶性固体についての議論を、それぞれが1種類の原子しか含まないため比較的単純な元素金属を考えることから開始します。 純金属は、金属原子が繰り返しパターンに密接に詰め込まれた結晶性固体である。 一般的な金属の性質である可鍛性や延性は、同じ原子が規則正しく並んでいることが大きな要因となっています。 ある金属と別の金属の特性の違いは、原子の大きさや空間的な配置の違いによって部分的に決まります。
金属の単位胞
金属であろうとなかろうと、結晶性固体の構造は、その最も単純な繰り返し単位(単位胞と呼ばれる)を考えることによって、最もよく説明されるものです。 単位胞は、原子またはイオンの位置を表す格子点からなる。 そして、図1に示すように、構造全体はこの単位胞が3次元的に繰り返されたものである。 左側は立方体で、各角に格子点、側面が単位セルで描かれている。 右側は同じ立方体をグレーアウトしたフォントで複製し、類似の立方体の無限のネットワークを示している。
結晶の格子構造と単位セルの調査を、最も単純な構造と最も基本的な単位セルから始めましょう。 これをイメージするために、テニスボールのような同じ球体を大量に取り出して、容器の中に一様に並べることを想像してください。 最も単純な方法は、図2に示すように、ある層の球体が、その下の層の球体の真上にあるような層を作ることであろう。 このような配置を単純立方構造といい、その単位セルを単純立方単位セルまたは原始立方単位セルと呼ぶ。

図2. 金属原子がある層の球の直上または直下に別の層の球を配置した場合、その格子構造は単純立方体と呼ばれる。 球体が接触していることに注意。
単純立方構造では、球体はそれほど密に詰まっておらず、容器の体積の約52%しか「満たして」いない。 これは比較的非効率的な配置で、単純な立方体構造では 1 つの金属 (ポロニウム、Po) しか結晶化しない。 図3に示すように、このような配置の固体は、各原子がその層にある4つの最近接原子と、その上の層にある真上の原子と、その下の層にある真下の原子だけに接触する面(層)で構成されている。 結晶性固体中の各粒子が接触する他の粒子の数は、その配位数として知られている。 したがって、単純な立方体配列のポロニウム原子の場合、配位数は6である。 左側は10.44の立方体の無限の積み重ねが今度は白黒で描かれているのみである。 ある格子点とそれに隣接する立方体の辺の線が非常に強調されています。 右側には、同じ図面が、今度は格子点を赤で、そこからの放射線を1-6とラベル付けしてある。
単純立方格子では、図4に示すように、すべての方向に繰り返される単位格子は、8個の原子の中心で定義される立方体である。 この単位格子の隣り合う角の原子は互いに接触しているので、このセルの辺の長さは2原子半径、つまり1原子直径に等しくなる。 立方晶のユニットセルには、これらの原子のうち、その中にある部分だけが含まれている。 単純な立方体の単位セルの隅にある原子は、合計8つの単位セルによって含まれるので、その原子の8分の1だけが特定の単位セル内にあることになる。 そして、単純立方単位セルの8つの「角」にはそれぞれ原子が1つずつあるので、1つの単純立方単位セル内には8個の⾵が存在する。 左側は10.45からの立方体単位が現れ、球形の灰色の分子が各格子点の上に重なっている。”simple cubic lattice cell “とラベルが付けられている。 右側は “8角 “とラベル付けされた同じ立方体単位で、この立方体単位の中に現れるであろう分子の球体の部分のみを示している
図4。 単純な立方格子の単位胞は、その8つの角のそれぞれに8分の1の原子を含むので、合計1個の原子を含む。
例1:金属の原子半径と密度の計算、その1
アルファポロニウムの単位胞の辺長は336pmである。
- ポロニウム原子の半径を求めよ。
- アルファポロニウムの密度を求めよ。
Check Your Learning
ニッケルのユニットセルの辺長は 0.3524 nmである。 ニッケルの密度は8.90g/cm3です。 ニッケルは単純な立方体構造で結晶化するか。 説明せよ。
ほとんどの金属結晶は4種類の大きな単位細胞のうちの1つである。 ここでは、図5に示した単純立方体、体心立方体、面心立方体の3種類の立方体単位セルに注目する(実際には7種類の格子系があり、中には2種類以上の格子を持つものもあり、合計14種類の単位セルがあることに注意されたい。 より複雑な形状はこのモジュールの後半に譲る。)

図5. 金属の立方体ユニットセルは、(上の図は)格子点の位置、(下の図は)ユニットセル内に位置する金属原子を示す。
図6のように、すべての角と中央に原子を持つ立方体ユニットセルという配列で結晶化する金属もある。 これを体心立方(BCC)固体と呼ぶ。 BCCユニットセルの角の原子は互いに接触せず、中央の原子に接触する。 BCCユニットセルには、8つの角のそれぞれ8分の1の原子(角から8回目の \frac{1}{8}=1 atom)と中心から1つの原子の合計2つの原子がある。 この構造では、どの原子も上の層の4つの原子と下の層の4つの原子に接しています。 したがって、BCC構造の原子は配位数が8です。

図6.立方体の外側の分子と赤い分子の断片が削られ、灰色の分子と赤い分子全体だけが残っている。 体心立方構造では、特定の層にある原子は互いに接触しない。 各原子はその上の層の4つの原子とその下の層の4つの原子に触れる。
BCC配列の原子は単純な立方体構造よりもはるかに効率的に詰まっており、全体の体積の約68%を占めている。 BCC構造を持つ同型金属としては、室温でK、Ba、Cr、Mo、W、Feなどがある。 (
アルミニウム、銅、鉛など他の多くの金属は、図7に示すように、すべての角と各面の中心に原子がある立方体の単位胞を持つ配列で結晶化する。 このような配列を面心立方(FCC)固体と呼ぶ。 FCCのユニットセルには4つの原子があり、8つの角にそれぞれ8分の1の原子(8times \frac{1}{8}=1 atom from the corners)、6つの面にそれぞれ2分の1の原子(6times \frac{1}{2}=3 atom from the faces)である。 角の原子は立方体の面の対角線に沿って隣接する面の中心にある原子に接触している。 原子は同一の格子点にあるので、同一の環境である。

図7.立方体の外側にある灰色の分子を削り取り、灰色の分子の一部と(半分に割ったので)6個の赤い分子を残している。 面心立方固体は、その名の通り、単位セルの面の角と中心に原子がある。
FCC配列の原子は、体積の74%を占める原子ができるだけ密に詰まっている。 この構造は立方最密充填(CCP)とも呼ばれる。 CCPでは、六角形に配列した原子が3層繰り返されている。 各原子は、自分の層で6個、上の層で3個、下の層で3個の原子と接触している。 この配置では、各原子は12個の近傍原子に接しているため、配位数は12となる。 FCCとCCPの配置が等価であることはすぐにはわからないかもしれませんが、なぜ同じ構造であるのか、図8で説明します。 最初の画像では、
と書かれた青い球の層を側面から見たもので、図8. CCP配列は六角形に並んだ原子が3層(ABCABC…)繰り返されたものである。 CCP構造の原子は、その層の6個の原子と、上の層の3個の原子、下の層の3個の原子と接触するので、配位数は12個になります。 視点を変えてみると、CCP構造は、A層の原子が1つの角に、B層の原子が対角線上に(2つの角と面の中央に)、C層の原子が残りの角にある面を持つユニットセルであることがわかる。 これは面心立方配列と同じである。
より密な充填は原子間の全体的な魅力を最大化し、全分子間エネルギーを最小化するので、ほとんどの金属中の原子はこの方法で充填される。 単純な金属結晶構造では、2 種類の最密充填が見られる。 図9に示す六方最密充填(HCP)と、すでに述べたCCPである。 どちらも原子が六角形に配列された層が繰り返される構造である。 どちらのタイプも、第一層(A)の上に第二層(B)が配置され、第二層の各原子は第一層の3つの原子と接触している。 第3層の位置づけは2通りある。 HCPでは,第3層の原子は第1層の原子の直上にあり(すなわち,第3層もタイプA),タイプAとタイプBの密着型積層(すなわち,ABABAB⋯)が交互に積層されている。 CCPでは、第3層の原子が第1、2層の原子の上にない(つまり、第3層はタイプC)、タイプA、タイプB、タイプCの密着層が交互に積層されている(つまり、ABCABC⋯)。 全金属の約2/3が配位数12の最密充填配列で結晶化する。 HCP構造で結晶化する金属はCd, Co, Li, Mg, Na, Znなど、CCP構造で結晶化する金属はAg, Al, Ca, Cu, Ni, Pb, Ptなどです。
図9と表示されている。 どちらのタイプの最密充填でも、原子は可能な限りコンパクトに詰められている。 六方最密充填は2つの層(ABABAB…)が交互に重なっている。
例題2:金属の原子半径と密度の計算 その2
カルシウムは面心立方構造で結晶化する。 単位格子の辺の長さは558.8pmです。
- この構造のCaの原子半径は何ですか。
Check Your Learning
銀はFCC構造で結晶化する。 その単位セルの辺の長さは409pmです。
- この構造におけるAgの原子半径は何ですか。
- Agの密度を計算します。
一般に、単位セルは、図10に示すように、3軸(a、b、c)の長さとそれらの間の角度(α、β、γ)により定義されている。 軸は、空間格子の点間の長さとして定義される。 その結果、単位セルの軸は同じ環境の点を結ぶ。

図10. 単位セルは3つの軸(a、b、c)の長さと軸間の角度(α、β、γ)で定義される。
格子系は7種類あり、中には2種類以上あるものもあり、合計14種類の単位セルがあり、図11のような形をしています。

図11. 7種類の格子系と14種類の単位セルがあります。
イオン結晶の構造
イオン結晶は、通常大きさの異なる2種類以上のイオンで構成されています。 これらのイオンの結晶構造への充填は、同じ大きさの金属原子の充填よりも複雑です。
ほとんどの単原子イオンは荷電球として振る舞い、反対電荷のイオンに対する引力はどの方向にも同じです。 その結果、イオン化合物の安定な構造は、(1)ある電荷のイオンをできるだけ多くの反対電荷のイオンが取り囲む場合、(2)カチオンとアニオンが互いに接触している場合、になります。
というラベルが付けられている(図12)。
単純なイオン構造では、通常、陽イオンよりも大きい陰イオンが最密充填配列で配置されているのがわかる。 (前に見たように、同じ原子核に引き寄せられる電子が増えるとアニオンが大きくなり、同じ原子核に引き寄せられる電子が減るとカチオンは原子に比べて小さくなります)。 小さい陽イオンは、陰イオンの間に残る2種類の穴(または間隙)のいずれかを占めるのが一般的である。 小さい方の穴は、ある平面上の3つのアニオンと隣接する平面上の1つのアニオンの間にある。 この穴を囲む4つのアニオンは、四面体の角に配置されているので、この穴は四面体穴と呼ばれる。 一方、より大きな穴は、八面体の角にある6つの陰イオン(1つの層に3つ、隣の層に3つ)の中心にあり、これを八面体穴と呼ぶ。 図12はこの2種類の穴を示したものです。
イオン化合物のカチオンは、カチオンとアニオンの大きさによって、図13に示すように四面体の穴と八面体の穴を占有することがあります。 比較的小さな陽イオンは四面体の穴を占め、大きな陽イオンは八面体の穴を占める。 陽イオンが大きすぎて八面体の穴に入らない場合、陰イオンは単純な立方体配列のような、よりオープンな構造をとることがある。

図13. 陽イオンの大きさと化合物が占める穴の形は直接関係している。
陰イオンのHCPまたはCCP配列では、各陰イオンに対して2つの四面体の穴が存在する。 アニオンの最密充填配列で結晶化する化合物は、四面体穴に陽イオンがある場合、陽イオンと陰イオンの比率は最大2:1であり、すべての四面体穴がこの比率で充填されていることになる。 例えば、Li2O、Na2O、Li2S、Na2Sなどがある。 2:1未満の化合物も、イオンの大きさが合えば、四面体穴に陽イオンと陰イオンが最密充填された配列で結晶化することがある。
例3:四面体穴の占有率
硫化亜鉛は亜鉛の重要な工業原料で、塗料の白色顔料としても使用される。 硫化亜鉛の結晶は、硫化物イオンが最密充填された配列で四面体穴の半分を亜鉛イオンが占めています。 硫化亜鉛の式は?
Check Your Learning
セレン化リチウムは、四面体のすべての穴にリチウムイオンがあるセレン化物イオンが最密充填した配列と表現することができる。 セレン化リチウムの式は?
HCP構造でもCCP構造でも八面体の穴とアニオンの比は1:1である。 したがって、アニオンの最密充填配列の八面体ホールにカチオンを持つ化合物は、最大でカチオン:アニオンの比率が1:1になり得る。 例えば、NiO、MnS、NaCl、KHなどでは、八面体の穴はすべて埋まっている。
例4:イオン化合物の化学量論
サファイアは酸化アルミニウムである。 酸化アルミニウムは、酸化物イオンの最密充填配列の八面体の穴の2/3にアルミニウムイオンがある状態で結晶化する。 酸化アルミニウムの式は何か。
Check Your Learning
白い顔料の酸化チタンは、酸化物イオンが最密充填配列した八面体の穴の半分にチタンイオンが入って結晶化する。 酸化チタンの式は?
アニオンの単純な立方配列では、配列中の各アニオンに対してカチオンが占めることのできる立方体の穴が1つある。 CsClや同じ構造を持つ他の化合物では、すべての立方体の穴が占有されている。 SrH2、UO2、SrCl2、CaF2では立方体の穴の半分が占められる。
異なる種類のイオン性化合物は、そのイオンの相対サイズと化学量論(構造を決定する二つの主要特徴)が似ている場合、同じ構造で結晶化することがよくある。
イオン性化合物のユニットセル
多くのイオン性化合物は立方体のユニットセルで結晶化し、これらの化合物を使用してイオン構造の一般的な特徴を説明します。
イオン性化合物が1:1の比率で似た大きさのカチオンとアニオンからなる場合、一般的に単純な立方構造を形作ります。 塩化セシウム(CsCl)(図14に図示)はこの例で、Cs+とCl-の半径はそれぞれ174 pmと181 pmである。 これは、セシウムイオンを中心とした単純な立方体の単位セルを塩化物イオンが形成していると考えることもできるし、塩化物イオンを中心とした単位セルをセシウムイオンが形成していると考えることもできるし、Cs+イオンが形成する単純な立方体の単位セルとCl-イオンが形成する単位セルが重なり合っていると考えることもできる。 セシウムイオンと塩化物イオンは、単位セルの対角線上に接している。 単位セルあたりセシウムイオンと塩化物イオンが1つずつ存在し、塩化セシウムの式で求められるl:lの化学量論が成り立っている。 セルの中心には格子点がなく、セシウムイオンと塩化物イオンは同一ではないので、CsClはBCC構造ではないことに注意。
これまで格子点の位置は任意であると述べてきた。 このことは、格子点がセシウムイオンの中心に位置しているCsCl構造の別の記述によって説明される。 この記述では、セシウムイオンはセルの角の格子点に位置し、塩化物イオンはセルの中心に位置しています。
イオン性化合物が、大きさが大きく異なる陽イオンと陰イオンの比率が1:1の場合、図15に示すようなFCC単位胞で結晶化するのが一般的である。 塩化ナトリウム(NaCl)はこの例で、Na+とCl-の半径はそれぞれ102 pmと181 pmである。 これは、塩化物イオンがFCCセルを形成し、ナトリウムイオンがセル端とセル中央の八面体の穴に位置していると考えることができます。 ナトリウムイオンと塩化物イオンは、セルエッジに沿って互いに接しています。 この単位格子は4個のナトリウムイオンと4個の塩化物イオンを含み、NaClという式で求められる1:1の化学量論を与えています。
Figure 15. NaClのような陽イオンよりはるかに大きい陰イオンを持つイオン化合物は、通常FCC構造を形成する。
立方晶の硫化亜鉛である閃亜鉛鉱も図16に示すようにFCCユニットセルで結晶化する。 この構造はFCC格子の格子点上に硫化物イオンを含んでいる。 (硫化物イオンの配置は、塩化ナトリウムの塩化物イオンの配置と同じである)。 亜鉛イオンの半径は硫化物イオンの半径の40%程度しかないため、これらの小さなZn2+イオンは交互に並ぶ四面体の穴、すなわち四面体の穴の半分に位置しています。 ユニットセルには4個の亜鉛イオンと4個の硫化物イオンがあり、経験式ZnS.

図16。 ZnS、硫化亜鉛(またはブレンデ亜鉛)は、硫化物イオンが格子点にあり、はるかに小さい亜鉛イオンが構造内の四面体の穴の半分を占めるFCC単位セルを形成します。
図17に示すようなフッ化カルシウム単位セルもFCC単位セルであり、この場合は陽イオンが格子点上に位置する;同等のカルシウムイオンがFCC格子の格子点上に配置される。 カルシウムイオンのFCC配列の四面体サイトはすべてフッ化物イオンによって占有されている。 化学式CaF2で求められるカルシウム:フッ素の比率はl:2であり、1つのユニットセル内に4つのカルシウムイオンと8つのフッ素イオンが存在することになります。 図17をよく見ると、カルシウムイオンが立方体の穴の半分にあり、フッ化物イオンが単純な立方体に配列していることがわかる。 フッ化物イオンはすべて同じ環境ではないので、フッ化物イオンの点の空間格子で構造を説明することはできない。 フッ化物イオンに対する4つのカルシウムイオンの向きは異なる。

図17. フッ化カルシウム,CaF2は格子点にカルシウムイオン(緑),その間の四面体サイトをすべてフッ化物イオン(赤)が占めるFCC単位セルを形成している。
イオン半径の計算
イオン性化合物の単位セルの辺長とセル内のイオンの位置がわかれば、個々のイオンの形と接触について仮定すれば、化合物中のイオンのイオン半径を計算することができる。
例5:イオン半径の計算
LiCl(NaCl類似構造、FCC)の単位セルの辺の長さは0.図15のように、リチウムイオンが十分に小さく、塩化物イオンが接触していると仮定して、塩化物イオンのイオン半径を計算する
注:長さの単位オングストロームは、しばしば原子レベルの寸法を表すのに用いられ、10-10 mに相当する。
Check Your Learning
KCl(NaCl類似構造、FCC)の単位セルの辺長は6.28 Åであり、セル辺に沿ってアニオン-カチオンの接触を仮定して、カリウムイオンの半径を計算しなさい。 塩化物イオンの半径は1.82Åです。
ユニットセルの辺の長さから計算したイオン半径の値は、イオンが完全球状など多くの仮定によっており、これらはせいぜい近似であることを認識することが重要です。 したがって、このような計算値はそれ自体近似的なものであり、比較はあまり厳密にはできない。
X 線結晶学
結晶中の単位格子の大きさや原子の配列は、X 線結晶学と呼ばれる、結晶による X 線の回折の測定から決定することができる。 回折とは、電磁波が光の波長と同じ大きさの物理的な障壁にぶつかったときに、進行方向が変わることである。
単色X線が結晶に当たると、その光線は結晶内の原子によってあらゆる方向に散乱されます。 同じ方向に進む散乱波が互いにぶつかると干渉を起こし、結合波の極大値の離れ具合によって振幅(強度)が増大したり減少したりする(図18参照)。 最初のセクションでは、2つの正弦波が示され、一方は他方の上に描かれ、一方の曲線の頂点から次の曲線の頂点までのセクションは、
図18とラベル付けされている。
ある波長λのX線が、距離dだけ離れた隣接する結晶面の原子によって散乱されるとき、それらが結合する前に2つの波が移動した距離の差が波長の整数倍、nであるとき、建設的干渉を起こす可能性がある。 この条件は、回折ビームの角度θが波長と原子間距離に関係するとき満たされる。
n{lambda }=2dtext{sin}theta
この関係は、この現象を最初に説明したイギリスの物理学者W. H. Braggにちなんでブラッグ方程式と呼ばれる。 図19は、同じ2つの結晶面からの回折波の2つの例である。 左の図はブラッグ角で回折した波で、建設的干渉を起こし、右の図はブラッグ条件を満たさない別の角度で回折し、破壊的干渉を起こしたものである
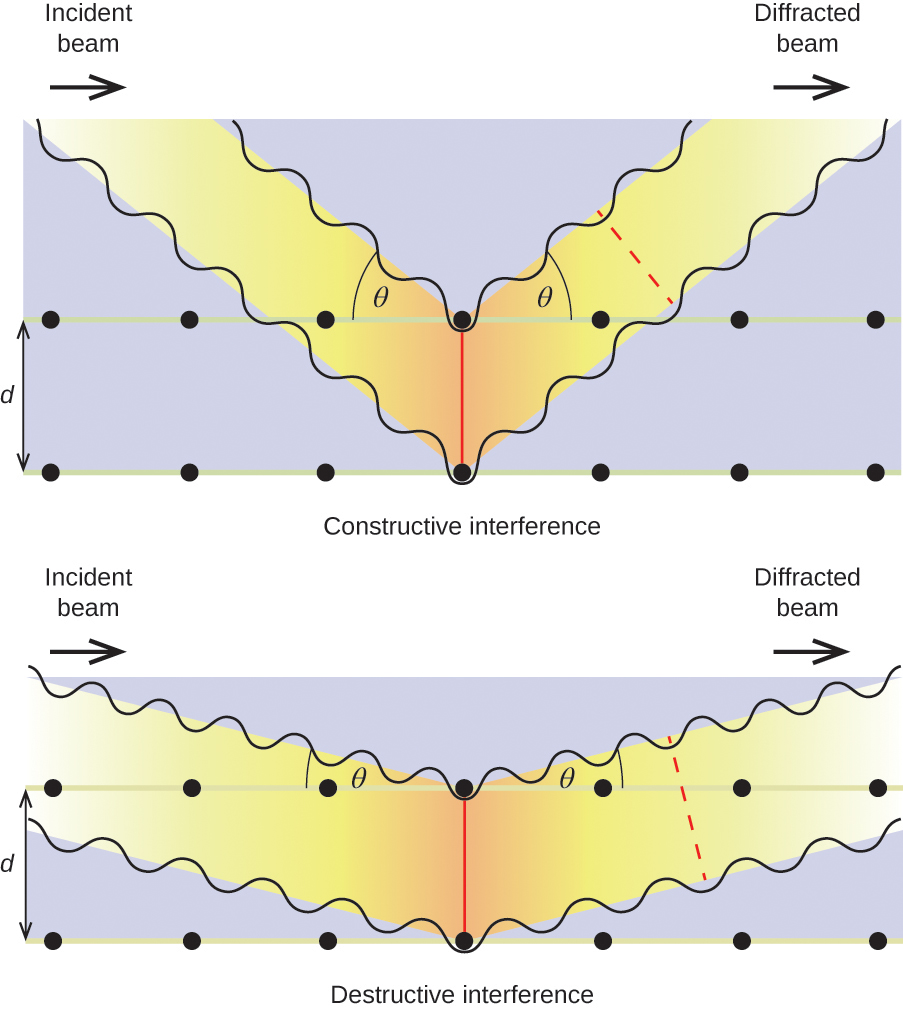
Figure 19と書かれている。 結晶内の原子によって散乱されたX線の回折は、原子間の距離を決定することを可能にする。 上の図は、2つの散乱波が建設的に干渉し、その結果、高い強度の回折波が発生する様子を示している。 下の図は、破壊的干渉と低強度の回折波です。
図20に示すようなX線回折計を使用して、上記のように結晶と相互作用したときにX線が回折する角度を測定することができる。 このような測定値から、ブラッグ方程式を使用して、以下の演習例で示すように、原子間の距離を計算することができる
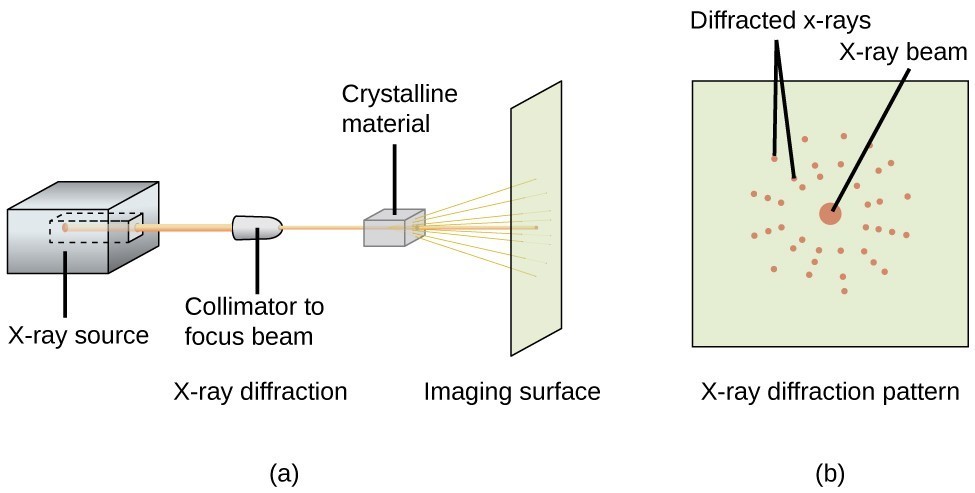
図20。 回折計(a)では、X線のビームが結晶材料に当たり、X線回折パターン(b)が得られ、これを解析して結晶構造を決定する。
「結晶学を祝う-アニメーションの冒険」の記録はこちらからご覧いただけます(新しいウィンドウで表示されます)。
例題6:ブラッグ式を使う
回折計で、波長0.1315nmのX線を用いて、銅の回折パターンを作製しました。 1次回折(n=1)は角度θ=25.25°で発生した。 銅の回折面の間隔を決定する。
Check Your Learning
面間が0.394nmの結晶は波長0.147nmでX線を回折します。 1次回折の角度は何度ですか?
ある化学者の肖像: X線結晶学者ロザリンド・フランクリン
図21.X線結晶学者ロザリンド・フランクリン
1953年、フランシス・クリックとジェームズ・ワトソンによるDNAの構造の発見は、科学史における偉大な業績の一つです。 彼らは、DNAの構造を実験的に証明したモーリス・ウィルキンスとともに、1962年にノーベル生理学・医学賞を受賞しています。 また、イギリスの化学者ロザリンド・フランクリンは、DNAのX線回折像を測定することで、この記念すべき業績に多大な貢献をした。 フランクリンは、そのキャリアの初期に、石炭の構造に関する研究で、イギリスの戦争に貢献した。 1950年代前半に生物学に目を向けると、博士課程の学生レイモンド・ゴスリングとともに、DNAが濡れているときにできる細長い繊維(B型)と乾燥してできる短くて幅の広い繊維(A型)の2つの形をしていることを発見した。 また、フランクリンは、ウイルスとその遺伝情報を含むRNAに関する先駆的な研究を行い、この分野の知識を根底から覆すような新しい情報を発見した。 卵巣がんを発症した後も、1958年に37歳で亡くなるまで研究を続けた。 その功績が認められ、シカゴのフィンチ健康科学大学医学部は2004年にロザリンド・フランクリン医学科学大学に改称し、彼女の有名なDNAのX線回折像を大学の公式ロゴに採用した。 金属原子は、六方最密充填構造、立方最密充填構造、体心構造、単純立方構造などに充填することができる。 単純なイオン構造では、アニオンはこれらの構造のいずれかをとるのが一般的で、アニオンの間に残った空間をカチオンが占める。 小さな陽イオンは通常、アニオンが最密充填された配列の四面体の穴を占有する。 大きな陽イオンは通常、八面体の穴を占める。 さらに大きな陽イオンは、単純な立方体配列の陰イオンの中にある立方体の穴を占めることができる。 固体の構造は、単位セルの大きさと形、およびセルの中身を示すことによって記述することができる。 構造の種類と単位胞の寸法はX線回折測定によって決定できる。
Key Equations
- n{lambda }=2dtext{sin}theta
Try It
- 立方単位胞に2つの等価金属原子を持つ結晶化した鉄の構造を説明しなさい。
- 立方体単位胞に4個の等価金属原子で結晶する白金の結晶構造を述べよ。
- クロムの体心立方構造におけるクロム原子の配位数は?
- アルミニウムの面心立方構造におけるアルミニウム原子の配位数は?
- コバルト金属は六方最密充填構造で結晶化する。 コバルト原子の配位数は?
- ニッケル金属は立方最密充填構造で結晶化します。
- タングステンは体心立方単位胞で結晶し、辺の長さは3.165Åです。
- この構造におけるタングステンの原子半径は何ですか。
- タングステンの密度を計算します。
プラチナ(原子半径=1.38Å)は立方最密充填構造で結晶化します。 面心立方単位胞の辺の長さと白金の密度を計算しなさい。
- この構造におけるバリウムの原子半径は?
- バリウムの密度を計算する。
- H-のイオン半径を計算しなさい。 (Li+のイオン半径は0.0.95Å)
- NaHの密度を計算する。
- TI+のイオン半径を計算します。 (I-のイオン半径は2.16Å。)
- TlIの密度を計算せよ。
- この物質の経験式は何であるか? 5613>
- Mn3+イオンの配位数は何ですか。
- Mn3+イオンの半径が0.65Aの場合、単位格子の辺長を計算しなさい。
- この化合物の密度を計算しなさい。
3 配位数とは、最近接の数をいう。 体心立方体の中心にあるクロム原子は、(立方体の角にある)8つの最近接原子を持ち、上の1平面に4つ、下の1平面に4つである。 六角形の最密充填は、各原子が12個の最近接に接するように行われます:自分の層で6個、隣接する各層で3個です。 したがって、配位数は12.
7 となる。 (a) 体心立方単位胞では、金属原子は立方体の内部の対角線に沿って接している。 内部の対角線は、ユニットセルの端と面の対角線とで直角三角形を形成している。 ピタゴラスの定理を使って、立方体の面の対角線の長さdを辺の長さeで求める。
d2 = e2 + e2 = 2e2
d = \sqrt{2} e
立方体の内側の対角線は原子半径4つ分の長さで、再びピタゴラスの定理を使って面対角と辺で計算することができる。
◇begin{array}{rll}left(\text{diagonal}}right)^2&=&d^2+e^2 ◇left(\sqrt{2} eright)+e^2 ◇2e^2=&3e^2 ◇e^2+e^2 ◇e^2=&&&{5>2e>
radius of tungsten = \frac{text{diagonal}{4}=⽯Sqrt{3}e}{4}left(3.165}=1.370};
(b) 体心立方構造で、各単位格子は2個の原子を含む。 単位セルの辺の長さを用いて、単位セルの体積と各原子が占める体積を計算する。 掛け算してモル体積を求め、この値で原子質量を割って密度(e=辺長)を求める:
V(cell) = e3 = (3.165 \times 10-8 cm)3 = 3.170 \times 10-23 cm3
V(atom) = \frac{3.170times {10}^{-23}{CM}}^{3}{text{2 atoms}}=1.0.585times {10}^{-23}{Text{cm}}^{3}{Text{atom}}^{-1}
V(mol) = 1.585 \times 10-23 cm3/atom \times 6.022 \times 1023 atoms/mol
= 9.585|V(分子)=1.546 cm3/mol
密度 = \frac{183.85{text{g mol}}^{-1}}{9.546{text{cm}}^{3}{text{mol}}^{-1}} = 19.26 g/cm
9. (a)体心立方単位胞において、金属原子は立方体の対角線に沿って接触している。 立方体の対角線は、ユニットセルの辺と面の対角線とで直角三角形を形成している。 ピタゴラスの定理を用いて、立方体の面の対角線の長さdをeの観点から求めよ。
d2 = e2 + e2 = 2e2
d = \sqrt{2} e
立方体の対角線は原子半径4つ分の長さで、再びピタゴラスの定理を使って計算することができる。
(diagonal)2 = (4r)2 = (2e)2 + e2 = 16r2 = 3e2
diagonal = 4r = \sqrt{3text{e}}
r = \frac{THREE}{4}text{e}=THREE}{3}}{4}
Diagonal = 4r = \frac{TREE}{3}} R = \frac{TREE}{3}}{3}{4} Diagonal = 489frac{TREE}{4}
(b) 体心立方構造で、各単位セルには2個の原子が含まれているものとする。 単位セルの辺の長さを用いて、単位セルの体積と各原子が占める体積を計算しなさい。 この値でグラム原子量を割って密度(e=辺の長さ)を求める。26884 ⑬frac{{10}^{-22}{{text{cm}}^{3}{text{atom}}^{text{-1}}}{2 atoms}} = 6.3442 ⑭times 10-23 cm3
V (mole) = 6.3442 ㎤ 10-23 cm3 ㎤ 6.022 ㎤ 1023 atoms/mol = 38.205 cm3
d(Ba) = \frac{137.33 g}{38.204 cm}^{3} = 3.595 g/cm3
11.Ba(Ba)=㎤ 10-23cm3<9133 Siの結晶構造から、Al(配位数12)よりも固体中の密度が低い(配位数4)ことがわかる
13. 最密充填配列では、各アニオンに対して2つの四面体穴が存在する。 四面体穴が半分しかない場合、アニオンとカチオンの数は等しくなる。 硫化カドミウムの式はCdS.
15 である。 酸化物イオンの最密充填配列では、各酸化物イオンに対して八面体正孔が1個、四面体正孔が2個存在する。 八面体穴の2分の1が埋まっていれば、酸化物イオン2個に対してCoイオンが1個存在することになる。 四面体の穴の8分の1が埋まっていれば、4つの酸化物イオンに対して1つのCoイオンが存在することになる。 酸化物イオン4個に対して、八面体の穴にはCoイオンが2個、四面体の穴にはCoが1個あるので、Co3O4.
17 という式になる。 単純な立方体配列では、配列中の各アニオンに対して1つの立方体ホールしかカチオンとして占有することができない。 タリウムとヨウ化物の比率は1:1でなければならないので、タリウムの式はTlI.
19となる。 最密充填配列では八面体正孔と酸素陰イオンの比は1:1である。 八面体正孔は2分の1しか占められていない。 したがって、チタンと酸素の比率は1:2となり、式はTiO2である。 構造中のTiの質量%は次の通りである:
percent Ti = \frac{47.90}{47.90+thext{2(15.9994)}}times \{100%}=thext{59.95%}
Ti1個に対してO2-イオン2個なのでチタンの酸化数は+4です。 両イオンとも大きさは近い。 Mgは0.65、Liは0.60です。 この類似性により、両者はむしろ容易に交換することができる。 電荷の差は、一般にSi4+とAl3+の入れ替えで補われる。 Mnイオンの総数は、コーナーとセンターからの寄与を加算して決定される。 Mn(コーナー):8㏄、Mn(センター)=1。 Mnの単位胞への寄与の合計=2.
Oの場合、立方体には合計12個の辺があり、辺の各イオンは単位胞に4分の1ずつ寄与する。 従って、O原子は12個㎤=3個となる。 その比率はMn:O=2:3で、式はMn2O3.
27となる。 ブラッグ方程式は次の通りである: nλ = 2d sin θ
where d is the spacing between planes.
d = \frac{n{lambda }}{text{2 sin}theta }=⑷frac{1(1. 1.541 A)}{2sin15.55^{Circ}}={1.541}Mathring{text}A}}{2(0.2681)}=2.874 Å
29.5Åを得た。 \θ=sin{θ}=θfrac{n{θlambda}}{2d}=θfrac{1)(0.2879}text{nm})}{2)(0.4164)}=3457なので、θ=sin-1(0.3457) = 20.2°
31になります。 ブラッグ方程式を用い、n=1、
λ=2dsinθ=2(2.64Å)sin 7.75=0.712Å
次にE=frac{hc}{lambda}=phrac{(6.626times {10}^{-34}} text{J s})(2.998times {10}^{8}{text{m s}}^{-1})}{0.712times {10}^{-10} text{m}} =2.79times {10}^{-15} text{J}=1.74times {10}^{4} text{eV}
Glossary
体心立方(BCC)固体:セルの角と中心に格子点を持つ立方体の単位格子を持つ結晶構造
体心立方単位格子の結晶構造。 体心立方結晶の最も単純な繰り返し単位で、各角と中心に格子点を持つ立方体である
Bragg equation: X線が結晶内の原子によって回折される角度に関する方程式
coordination number: 結晶中の任意の原子または錯体の中心金属原子に最も近い原子数
cubic closest packing (CCP); CCPは、結晶中の任意の原子に最も近い原子を含む。 結晶構造は、原子やイオンが密に詰まった面が、相対的な向きが異なる3つの層が交互に積み重なったもの(ABC)
diffraction: 回折。
回折:電磁波が適切な寸法の物理的障壁に遭遇したときに起こる電磁波の再配向
面心立方(FCC)固体:各面の角と中心に格子点を持つ立方体の単位セルからなる結晶構造
面心立方単位セル。 面心立方結晶の最も単純な繰り返し単位。各角と各面の中心に格子点を持つ立方体である
hexagonal closest packing (HCP): 原子またはイオンの密着した層が、異なる相対方位の2層交互のシリーズとして積層されている結晶構造(AB)
hole: 孔。 (間隙):結晶内の原子間の空間
isomorphous: 同じ結晶構造を持つ
octahedral hole: 八面体の角にある6つの粒子の中心にある結晶内の空間
simple cubic unit cell: 単純な立方体の単位セル。 (原始立方単位セルとも)単純立方構造の単位セル
simple cubic structure: 角にのみ格子点を持つ立方体単位セルの結晶構造
space lattice: 同一環境を持つ結晶内のすべての点
tetrahedral hole: 結晶内の空孔:
単位胞: 結晶中の4つの原子またはイオンによって形成される四面体の空間
X線結晶学: 結晶を通過するときにX線が回折する角度を測定し、結晶中の原子間の距離を決定する実験技術
結晶中の原子: 結晶中の3次元的に繰り返されて格子全体を形作る最小の部分
結晶中の原子間の距離: X線が格子全体を通るときに回折された角度を測定し、原子間の距離を決定する実験技術
単位胞


