キャラクターテーブルって何の役に立つのでしょうか。 簡単な答えは、分子の対称性と関連する特性表は、結合だけでなく、化学的に重要な分光学の多くの側面を解釈し、予測するために使用することができるということです。

実験室では、赤外線 (IR) やラマン分光法を使って有用な実験データを収集することができます。 このデータは、群論と正しい文字表の適用から予測されるIRやラマンの活性バンドの数と比較することができます。 この処理の背後にある数学（群論と行列代数）は、強固な理論的基盤として機能する。 分子のすべての対称操作は数学的な群を構成し、群の規則に従うので、以下に説明する操作はうまくいく。

分子の自由度と振動

ここでは、まず単純な分子（水）の自由度について説明する。 より大きな分子を調査する際に、なぜ対称性を採用することが非常に有益であるかがすぐにわかるでしょう。

「N」個の原子を持つ分子では、3N の自由度があります（私たちが x、y、z 座標の 3 次元の世界に住んでいることを覚えておいてください）。 非線形分子の場合、3つの自由度は並進、つまり体全体の動き（Tx, Ty, Tz）、3つは回転（Rx, Ry, Rz）に署名することができます。 残りの原子の運動は、原子の平均位置からの変位であり、重心は変化しない。 これらの基本振動は「通常モード」と呼ばれる。 従って、非線形分子は3N-6個の通常モードを持つことになる。 水の場合は、3×3-6＝3個である。

水に関しては、もちろん集中的に研究されているので、3つの振動は以下の通りであることが分かっている。 つまり、分子の性質である振動は、対称種や既約表現で記述できるのである。 実際、振動分光学に関する文献の多くは、情報を伝達するための略記法としてこれらの記号を用いています。

分子内の原子数がわずかに増加するだけで、振動の数が急激に増加することは明らかでしょう。 水について行ったように、振動の種類を目で見て判断することは、今ではかなり難しくなっています。 例えば、次のような化合物を考えてみよう。

H2O 3原子3振動

PH3 4原子6振動

CO22- –

H2O 3原子3振動

PH3 4原子6振動

H2O 3原子3振動

XeF4 5原子9振動

B2H6 8原子18振動

D2h対称のジボラン（B2H6）について、18振動全ての性質と対称性を調べるのは大変な作業であろう。

水の場合、分子特性の欄に3つの振動（ν1、v2、v3）をリストした特性表（C2v）を以下に示すように提示することができる。 (ν＝ギリシャ記号「ヌ」）

しかし一般にこの方法は非現実的である。 たとえばピリジン（C5H5N）。 点群もC2vであるが、分子には11個の原子がある。 基本振動モードの数は27（3×11-6＝27）である。

この場合、27個すべての振動の対称性を示すC2v特性表を作成しなければならないでしょう。 このような理由から、通常、振動はキャラクタテーブルに含まれない。 その代わりに、ユーザー（あなた）は、遭遇するあらゆる分子の振動の数と種類（その対称性によって定義される）を決定することができるのである。 その方法を以下に説明する。

Reducible Representations

前に述べたように、文字テーブルの重要な特性の1つは、対称演算が数学的グループのメンバーであり、それらの間に重要な関係が存在するということである。 一般に同じことが、分子の性質の対称種または既約表現についても言える。 既約表現の文字を乗算または加算・減算で組み合わせた積もまた、群の規則に従う。 新しい表現はもはや可能な限り単純なものではなく、その構成要素に「還元」できることから「還元可能表現」と呼ばれる。

たとえば、水の場合、並進の対称性 (Tx, Ty, Tz) は C2v 文字表から直接得ることができる。 それらはA1,B1,B2である。 これらの3つの自由度をすべて表現ΓTで表すと、以下のような式が書ける。 (Γ＝ギリシャ文字の大文字「ガンマ」）.

ΓT = A1 + B1 + B2

A1、B1、B2は単に対称種（既約表現）の省略表記であることが分かります。 したがって、C2vの文字表からA1、B1、B2の各文字を足してΓTの文字を書くだけです。

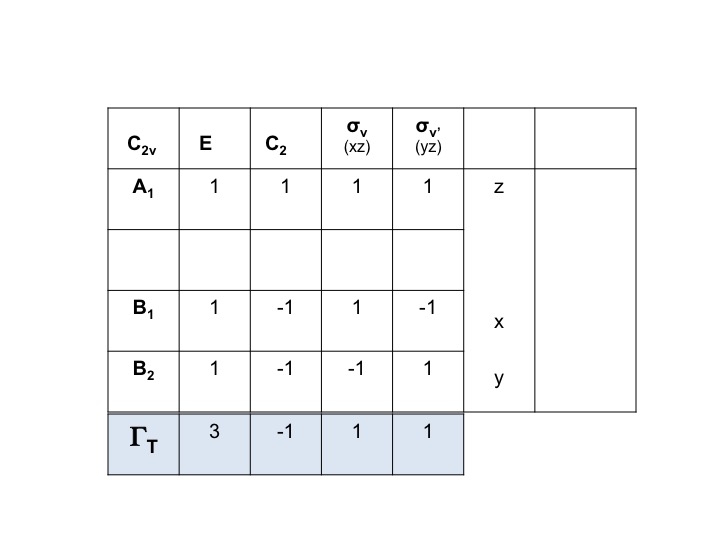
したがってΓT = 3 -1 1となります。

これは有効な還元可能表現で、C2v群のメンバーです。

同様の方法で、3つの回転とすべての振動の還元可能表現を書き下すことができます。

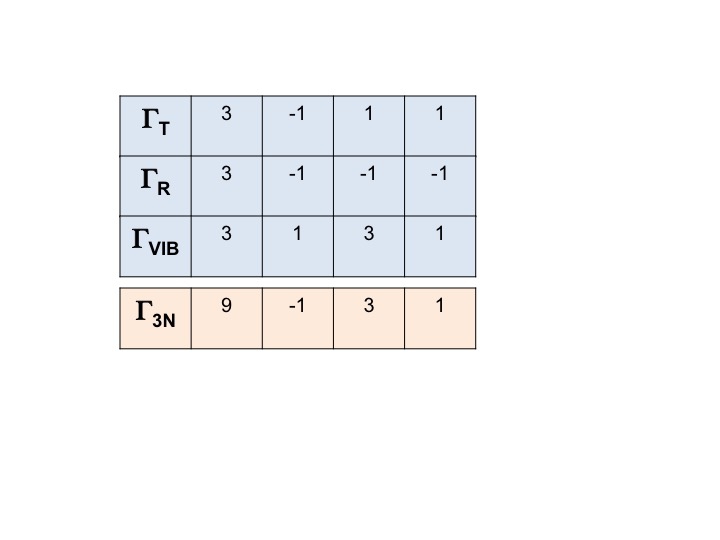
分子（3N）の全自由度の表現は

Γ3N = ΓT + ΓR + ΓVIB

と書き、これに対する還元可能表現は単にΓT、ΓRおよびΓVIBの文字の合計で得られます。

Γ3N = 9 -1 3 1

Make a note of this – it will come up later!

The set of characters 9 -1 3 1 is a valid member of the C2v group although it is not particularly useful when discussed of molecular properties. 本当に必要なのは、省略形の対称種（マリケン記号、A1、B1など）の言語です。 つまり、Γ3NをA1、B1などで表現したいのです。 6309>

Γ3N = 3A1 +A2 + 3B1 +2B2

良いニュースは、他のより複雑な分子については、我々は検査によってこのタスクを実行する必要がないことです：

1. 分子の還元可能表現としてΓ3Nを簡単に生成できる（その点群対称性がわかっていれば）

2. 還元式として知られる「簡単な」式を用いて、Γ3N還元可能表現をその対称種（マリケン記号）の和に簡単に変換することができる。

Γ3Nを求める一般的な方法

ステップ1

分子の文字表を取り、一番下に行を追加する。 この行に、x, y, z の分子特性に対応する各操作の文字を加えるだけで、上でやったようにΓT（またはΓxyz）の還元可能な表現を生成することができます。 C2vについては、これらがA1、B1、B2に対応する文字であることを既に示しました。

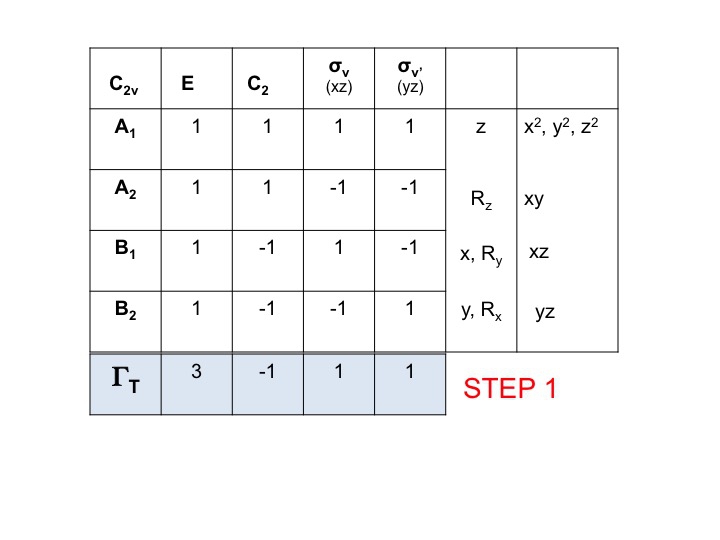
ステップ2 ΓTの下にもう1行追加して、各対称操作で位置を変えない原子の数を書き入れます。 ここで、実際の分子モデル・セットがいかに有用であるかがわかる。 このためには、対称要素がどこにあるのか、対称操作が分子にどのような影響を与えるのかを知っておく必要があります。 もちろん、あなたはSchönflies記法を勉強し、分子の点群の割り当て方を知っているので、すでにこの方法を知っています。

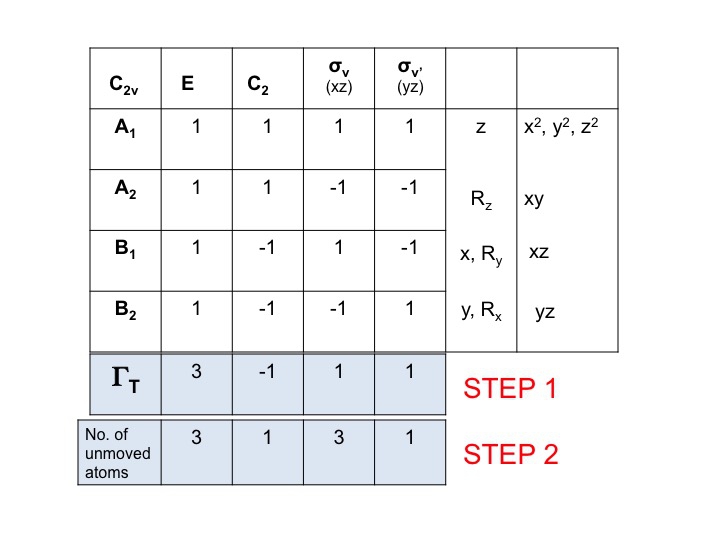
したがって、水（3原子）についてはEの下に3つの動かない原子がありますが、C2については両方のHが動きますが、O原子はC2軸に座っているのでその場所は変わらず、したがってC2列の下に1を記録することになります。 ステップ2で生成された新しい数字の集合（3 1 3 1）もC2vの還元可能表現であり、グループの規則に従う。

ステップ3

このステップでは、ステップ1および2で生成した文字を単に掛け合わせるだけである。 結果（3行目）は、Γ3N（またはΓTOT）の還元可能な表現です。

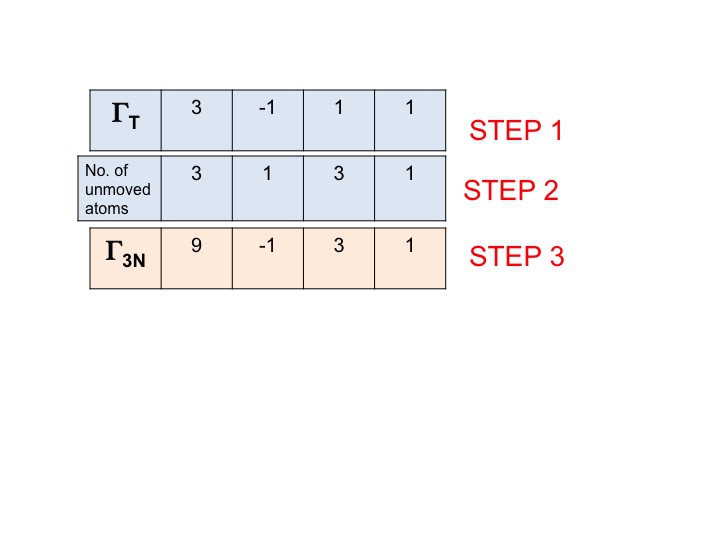
新しい還元可能表現 (9 -1 1 3) は、前に調べて得た Γ3N の表現と同じであることに気が付くでしょう。

還元可能表現の縮小

任意の還元可能表現をその還元できない表現（対称種やマリケン記号）の和に変換するには縮小公式を使います：

この情報は文字テーブルで簡単に見つけられます：

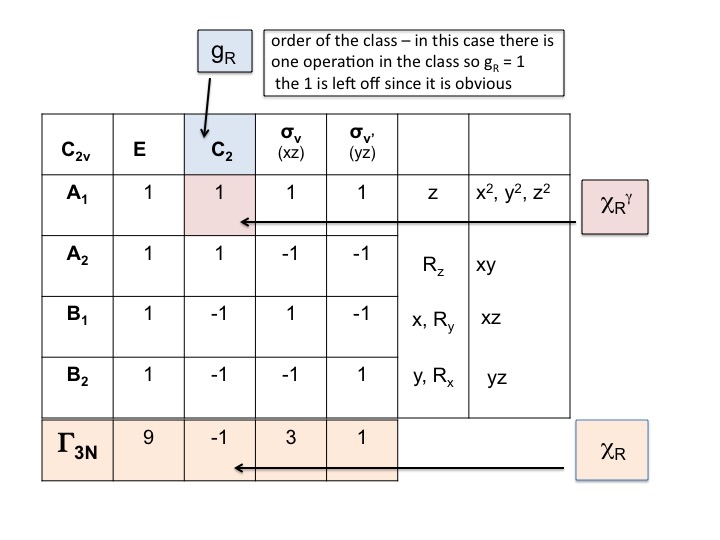
水の例に戻ってください。 点群C2v, 位数(g) = 4

Γ3N = 9 -1 3 1

この表現でのA1の出現回数は

aA1 = 1/4 { 1.1.9 + 1.1. (-1) + 1.1.3 +1.1.1} = 3

ですからΓ3Nは3つのA1対称種を含んでいます。 他の対称種の数は次のように計算されます：

aA2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1).3 + 1.(-1).1 } = 1 A2 存在

aB1 = 1/4 { 1.1.9 + 1.(-1). (-1) + 1.1.3 + 1. (-1).1} = 1 A1.1

aA2 = 1/2 { { 1.1.9 + 1.1. (-2).3 + 1. = 3 3 B1 present

aB2 = 1/4 {1.1.9 + 1.(-1)(-1) + 1.(-1).3 + 1.1.1} となります。 = 2 2 B2存在

これで、Γ3N = 3A1 + A2 + 3B1 + 2B2（上の「検査」で得たのと全く同じ。 ここで、並進と回転の対称種を引くと、基本振動モードの数と対称種が求まります。 ΓTとΓRは、文字表から直接求めることができる。

γ3n = 3a1 + a2 + 3b1 + 2b2

γt = a1 + b1 + b2

γr = a2 + b1 + b2

γvib = γ3n –

γvib = γ1 + b2

γt = a1 + b2 + 2b2

γt = a1 + b1 + b2 ΓT – ΓR = 2A1 +B1

従って、水の3つの通常振動モードは、対称性A1, A1、B1です。

これで、分子の基本振動モードをすべて決定し、それをマリケン記号という略語で表現する一般的な方法ができたわけである。 これは試験1で出題される演習の一つです。 この方法に自信を持つには、可能な限り多くの例を練習することです！

Next: 選択ルール