17世紀と特に18世紀の間に、気体の特性は、そのような気体の法則を使用するようになりました。 自然を理解したいという欲求と、自分たちが飛べる気球を作りたいという欲求の両方から、多くの科学者が気体のマクロな物性、すなわち圧力、体積、温度、気体量の関係を確立した（図1）。 その測定は、今日の基準からすると決して正確なものではなかったが、彼らは、これらの変数の組（圧力と温度、圧力と体積など）が、理想気体（実際の気体がある条件下で近似する仮想の構成要素）において成立する数学的関係を決定することができたのである。 この法則は、気体の気体量を関係付けるもので、低圧と中温では極めて正確である。 ここでは、個々の関係における重要な発展（教育的な理由から、歴史的な順序にはこだわらない）を検討し、それらを理想気体の法則にまとめていく。 1783年、（a）水素充填気球の初飛行、（b）有人熱気球の飛行、（c）有人水素充填気球の飛行が行われた。 (a)の水素充填気球が着陸したとき、怯えたゴネスの村人たちは投石器とナイフで破壊したと伝えられている。 後者の打ち上げは、パリで40万人の観衆が見たと伝えられている。

圧力と温度: ゲイ＝リュサックの法則

圧力計を取り付けた硬い容器にガスを入れ、ガスを逃がさないように容器を密閉することを想像してください。 容器を冷やすと中の気体も同様に冷えて、圧力が下がるのが観察されます。 容器が硬く密閉されているので、気体の体積とモル数は一定である。 球体を加熱すると、中の気体は高温になり（図2）、圧力が上昇する。 温度が気体の圧力に与える影響：ホットプレートがオフの時は、球体の中の気体の圧力は比較的低い。

このような温度と圧力の関係は、一定の体積に閉じ込められた気体のサンプルであれば、どこでも見られることである。 このような条件下での空気の試料の圧力-温度データの実験例を図3に示す。 温度と圧力は直線的な関係にあり、温度がケルビンスケールであれば、PとTは正比例し（これも気体の体積とモル数が一定であれば）、ケルビンスケールの温度がある係数だけ上昇すれば、気体の圧力は同じ係数だけ上昇することがわかる

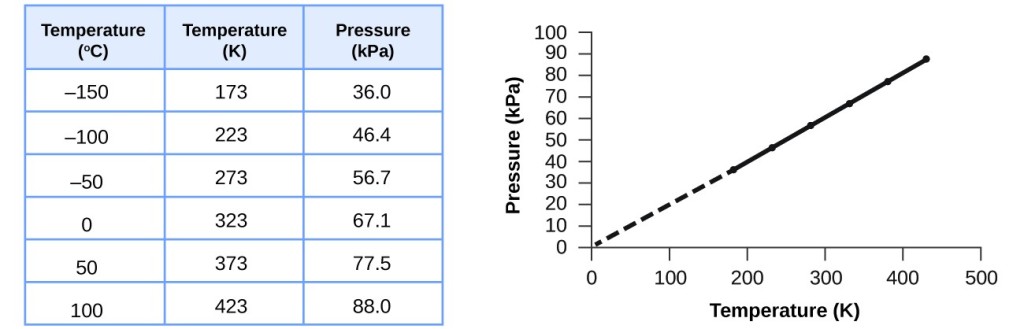
図3. 空気の体積と量が一定であれば、温度がケルビン単位であれば、圧力と温度は正比例する。 (これより低い温度では気体が凝縮してしまうため測定できない)。 この直線を低圧に外挿すると、-273℃で圧力0になる。これはケルビンスケールで0であり、絶対零度と呼ばれる最低温度である。

ギヨーム・アモントンは気体の圧力と温度の関係を初めて経験的に確立した（～1700）し、ジョセフ・ルイ＝リュサックがより正確にその関係を決定（～1800）した。 このことから、気体の圧力と温度の関係は、ゲイ＝リュサックの法則、あるいはアモンソンスの法則と呼ばれる。 どちらの法則でも、体積を一定にしたとき、一定量の気体の圧力はケルビン温度に正比例するとされている。 Mathemically, this can be written:

large Ppropto T

large P=text{constant}times T

large P=kenta T

where ∝ は「に比例する」、k はガスの同一性と量と体積に依存する比例定数である。

largefrac{{P}_{1}}{{T}_{1}}=themefrac{{P}_{2}}{{T}_{2}}

この式は定容の気体の圧力-温度計算で有用である。 気体の法則の計算では、温度はケルビンスケールでなければならないことに注意してください（ケルビンスケールで0、可能な限り低い温度を絶対零度と呼びます）。 (また、気体の温度が変わると圧力がどのように変化するかを記述するには、少なくとも3つの方法があることに注意してください。 値の表、グラフ、数式です。）

体積と温度。 シャルルの法則

風船に空気を入れて密閉すると、大気圧、たとえば1気圧のとき、風船には一定量の空気が入っています。 この風船を冷蔵庫に入れると、中の気体が冷えて風船は縮みます（ただし気体の量と圧力は一定）。

一定の圧力で閉じ込められた気体の体積に対する温度の影響の例は、一般に当てはまります。 温度が高くなると体積は増加し、低くなると減少する。 1気圧のメタンガスの1モルの体積-温度データを列挙し、図4にグラフ化した。 1気圧一定で1モルのメタンガスの場合、体積と温度は直線的な関係にある。 温度がケルビンの場合、体積と温度は正比例する。 外挿するとグラフの原点と交差し、絶対零度を表す。

一定圧力で一定量の気体の体積と温度の関係は、フランスの科学者、気球飛行の先駆者ジャック・アレクサンドル・セザール・シャルルの名をとってシャルルの法則と呼ばれている。 シャルルの法則とは、圧力を一定にしたとき、一定量の気体の体積はケルビン温度に正比例する、というものである。

Mathematically, this can be written as:

large Vpropto T

large V=text{constant}cdot T

large V=kenta cdot T

with k is a proportionality constant that depends on the amount and pressure of the gas.

large {frac{V}_{1}}{{T}_{1}}={frac{V}_{2}}{{T}_{2}}

体積と圧力：ボイルの法則

気密注射器に一部空気を入れると、一定温度、例えば25℃で一定量の空気が入っていることになります。 温度を一定に保ったままゆっくりとプランジャーを押し込むと、注射器内の気体はより小さな体積に圧縮されて圧力が上がり、プランジャーを引き抜くと体積は増えて圧力は下がります。 このように、一定量の気体を閉じ込めたときの圧力に体積が影響する例は、一般的に言えることです。 気体の体積を減らせば圧力は上がり、体積を増やせば圧力は下がります。 実際、体積がある割合で増加すると、圧力は同じ割合で減少し、その逆もまた然りである。 室温の空気の体積と圧力のデータを図5に示す。 気体は小さい体積を占めると高い圧力を出し、大きい体積を占めると低い圧力を出す(気体の量と温度は変化しないと仮定)。 PとVは反比例するので、1/P vs Vのグラフは直線になります。

P-T、V-Tの関係とは異なり、圧力と体積は正比例ではありません。 その代わり、PとVは反比例を示す。 圧力を上げると、気体の体積は減少する。 Mathemically this can be written:

Large Ppropto 1}Text{/}V}text{ or }P=k}cdot 1}Text{/}V}text{ or }{P}_{1}{V}_{1}={P}_{2}{V}_{2}

ただしkは定数とする。 図式的には、この関係は圧力(V)に対して圧力(V)の逆数(P)をプロットすると直線で示され、また圧力(V)に対して体積(V)の逆数(V)をプロットすると直線で示されます。 曲線グラフは変数の値が小さいときや大きいときに正確に読み取ることが難しく、実験データに理論式やパラメータを当てはめる際に使いにくくなる。 このような理由から、科学者はしばしばデータを「線形化」する方法を見つけようとする。 PとVをプロットすると双曲線になる（図6参照）。

一定温度での一定量の気体の体積と圧力の関係は、300年以上前にイギリスの自然哲学者ロバート・ボイルが初めて発表しました。 現在ではボイルの法則として知られている文章に要約されている。

Chemistry in Action: 呼吸とボイルの法則

あなたは一生、1分間に約20回、休みなく、多くの場合、意識することなく、何をしているのでしょうか？ 答えはもちろん、呼吸、すなわち呼吸です。 その仕組みはどうなっているのでしょうか。 それは、気体の法則が適用されるからです。 肺は、体に必要なガス（酸素）を取り込み、老廃物（二酸化炭素）を排出します。 肺はスポンジのような伸縮性のある組織でできていて、呼吸するときに膨張と収縮を繰り返します。 息を吸うとき、横隔膜と肋間筋（肋骨の間の筋肉）が収縮し、胸腔が広がって肺の容積が大きくなります。 容積が大きくなると、圧力が低下します（ボイルの法則）。 これにより、空気が肺の中に流れ込みます（高圧から低圧へ）。 息を吐き出すときは、この過程が逆転します。 横隔膜と肋骨の筋肉が緩み、胸腔が収縮して肺の容積が減少し、圧力が上昇して（再びボイルの法則）、空気が肺から流れ出します（高圧から低圧へ）。 その後、息を吸っては吐いてを繰り返し、このボイルの法則のサイクルを一生繰り返す（図7）

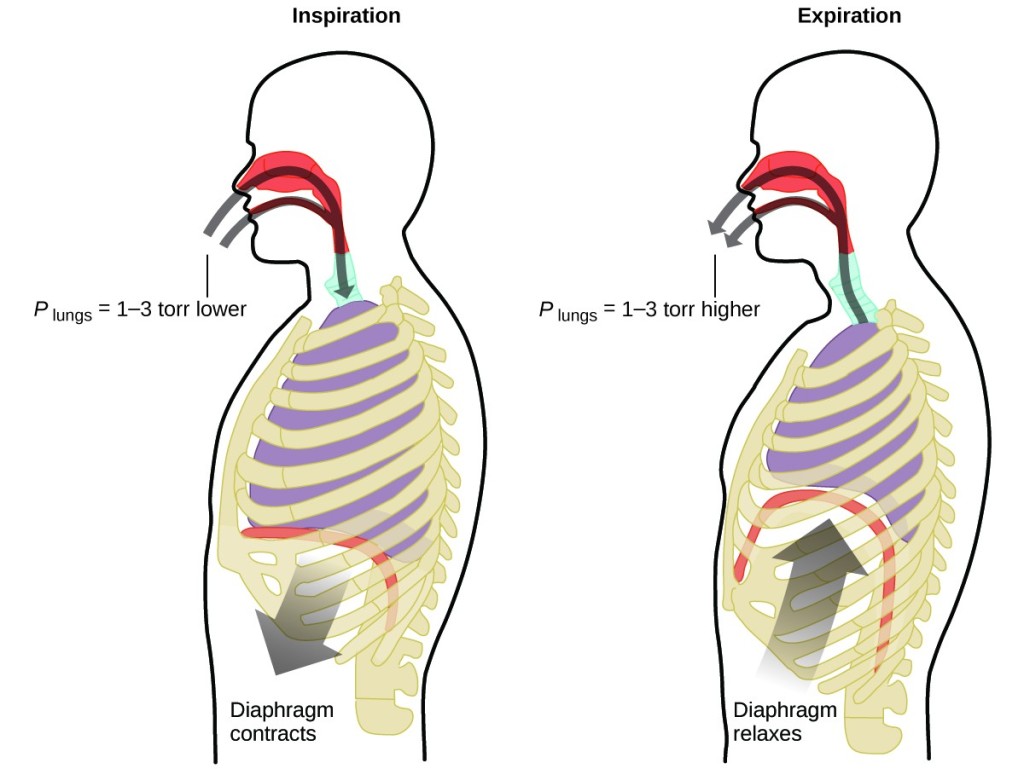
図7. 呼吸が起こるのは、肺の容積の膨張と収縮によって、肺と周囲の間に小さな圧力差が生じ、空気が肺に吸い込まれたり、肺から押し出されたりするからです。

気体のモルと体積。 アボガドロの法則

イタリアの科学者アメデオ・アボガドロは、1811年に気体の挙動を説明するために、温度と圧力が同じ条件で測定したすべての気体の等量は、同じ数の分子を含んでいるという仮説を提唱しました。 この関係は、やがて多くの実験結果によって裏付けられ、アボガドロの法則として表されるようになった。 閉じ込められた気体では、圧力と温度が一定であれば、体積(V)とモル数(n)は正比例する。

これを式にすると次のようになる。

largebegin{array}{cccc}V}propto n& \text{or}& V=k³³times n& \text{or}

他の変数の組についても、数学的関係を決定することが可能である。 P対n、n対Tのような。

このインタラクティブな PhET シミュレーション リンクを使用して、圧力、体積、温度、および気体の量の間の関係を調べます。 シミュレーションを使用して、（さまざまな気体の法則に関する前のセクションで説明したように）他のパラメータを一定に保ちながら、あるパラメータを変更すると他のパラメータにどのような影響が及ぶかを調べます。

アボガドロの法則：温度と圧力が一定のときの気体の体積は気体分子の数に比例する

ボイルの法則：温度が一定で与えられたモル数の気体の体積は測定した圧力に反比例する

シャルルの法則：温度と圧力が一定で与えられたモル数の気体の体積は圧力に反比例する

ボイルは、気体分子の数に比例する

ボイルの法則：温度が一定で与えられたモル数の気体が測定した圧力に反って、気体分子の数に比例して、気体分子の数が増える。 モル数の気体の体積は、圧力が一定ならケルビン温度に正比例する

Gay-Lussac’s law: 気体の体積は、圧力が一定ならケルビン温度に正比例する。 (気体のモル数が一定であれば、圧力はケルビン温度に正比例する

。