以下略です。.. ![]()
![]()
ピタゴラス3連とは,正の整数 ![]() ,
, ![]() ,
, ![]() の3つで,脚
の3つで,脚 ![]() と斜辺
と斜辺 ![]() とをもつ直角三角形が存在するようなものである. ピタゴラスの定理により、これは
とをもつ直角三角形が存在するようなものである. ピタゴラスの定理により、これは
| |
(1)
|
最小で最も有名なピタゴラス三重は ![]() である。 7670>
である。 7670> 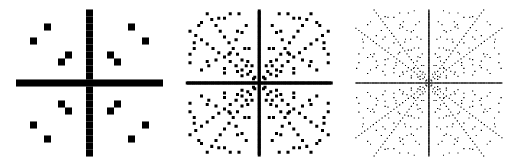
![]() がピタゴラス三角となる
がピタゴラス三角となる ![]() 面上の点のプロットは上に示すように、境界が次第に大きくなるように描かれています。
面上の点のプロットは上に示すように、境界が次第に大きくなるように描かれています。

同様に ![]() がピタゴラス3角形となる
がピタゴラス3角形となる ![]() 面の点のプロットも逐次大きくして上に示すようにする。
面の点のプロットも逐次大きくして上に示すようにする。

![]() と
と ![]() が相対素数のピタゴラス三重奏は、原初的なものから他の解が自明的に生成できるため、「縮小」三重奏だけを考えるのが一般的である。 上の図は原始三重構造を示したものであるが、原始三重構造に対応する放射状の線はこの図にはないことがすぐにわかる。 原初的な解は
が相対素数のピタゴラス三重奏は、原初的なものから他の解が自明的に生成できるため、「縮小」三重奏だけを考えるのが一般的である。 上の図は原始三重構造を示したものであるが、原始三重構造に対応する放射状の線はこの図にはないことがすぐにわかる。 原初的な解は![]() か
か![]() のどちらかが偶数で、もう一方が奇数でなければならない(Shanks 1993, p.141)、
のどちらかが偶数で、もう一方が奇数でなければならない(Shanks 1993, p.141)、![]() は常に奇数でなければならない。
は常に奇数でなければならない。
さらに、ピタゴラス3連の1辺は3で、4で、5で割り切れるが、(8, 15, 17), (7, 24, 25), (20, 21, 29) のように1辺が2つの場合もあり、 (11, 60, 61) のように3つすべてを持つ場合もある。
原始三重![]() があると、
があると、
|
(2)
|
|||
|
(3)
|
|||
|
(4)
|
where
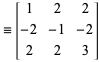 |
(5)
|
|
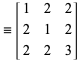 |
(6)
|
|
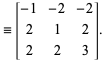 |
(7)
|
Hall (1970) と Roberts (1977) は ![]() is a primitive Pythagorean triple iff
is a primitive Pythagorean triple iff
|
(8)
|
ここで ![]() は行列
は行列 ![]() ,
, ![]() ,
, ![]() の有限積とする。 したがって、すべての原始ピタゴラス三重奏は無限配列
の有限積とする。 したがって、すべての原始ピタゴラス三重奏は無限配列
 |
(9)
|
ピタゴラスとバビロニア人は、(必ずしも原始的ではない)三角形の生成公式を
|
(10)
|
for ![]() , which generates set of distinct triple contains neither all primitive or all imprimitive triple (and where in special case
, which generates set of distinct triple contains neither all primitive or all imprimitive triple (and where in special case ![]() ,
, ![]() ).
).
初期ギリシャ人は
|
(11)
|
ここで ![]() と
と ![]() は比較的素で反対のパリティ (Shanks 1993, p.25) とした。 141)、これは(適切に
は比較的素で反対のパリティ (Shanks 1993, p.25) とした。 141)、これは(適切に![]() と
と![]() を並べた後に)正確に原始三重項を含む明確な三重項のセットを生成する。
を並べた後に)正確に原始三重項を含む明確な三重項のセットを生成する。
![]() をフィボナッチ数とする。 すると
をフィボナッチ数とする。 すると
|
(12)
|
は原始三重・非原始三重ともに網羅的ではないが、明確なピタゴラス三重を生成する (Dujella 1995)。 より一般的には、正の整数![]() ,
, ![]() から始めて、
から始めて、![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , ・・・を条件としてフィボナッチ的数列
, ・・・を条件としてフィボナッチ的数列![]() が構成できる。 は、異なるピタゴラスの三角形
が構成できる。 は、異なるピタゴラスの三角形
|
(13)
|
(Horadam 1961), where
|
(24)
|
(Beiler 1966, p. 116). なお、![]() は、
は、![]() が素数か2回素数である場合。
が素数か2回素数である場合。 ![]() , 2, …の最初の数列は0, 0, 1, 1, 1, 1, 2, 1, 4, 1, …である。 (OEIS A046079).
, 2, …の最初の数列は0, 0, 1, 1, 1, 1, 2, 1, 4, 1, …である。 (OEIS A046079).
ある数![]() が原始直角三角形の斜辺になる方法
が原始直角三角形の斜辺になる方法![]() の数を求めるには、その因数分解を
の数を求めるには、その因数分解を
|
(25)
|
ここで ![]() s は
s は ![]() 形式、
形式、![]() sは
sは ![]() 形式である。 このとき可能な原始直角三角形の数は
形式である。 このとき可能な原始直角三角形の数は
| |
(26)
|
例えば、以下のようになります。 ![]() since
since
|
(27)
|
|||
|
(28)
|
![]() ,2,…に対する
,2,…に対する![]() の値は0、0、0,1、0、0、0、1、0、0,1,…である。 (となります(大日本印刷 A024362)。 4497>4x+1の形の最初の数個の素数は、5、13、17、29、37、41、53、61、73、89、97、101、109、113、137、……である。 (OEIS A002144)であるから、1、2、4、8、16、…の原始直角三角形の斜辺となる最小の辺の長さは5、65、1105、32045、1185665、48612265、…である。 (です(OEIS A006278)。
の値は0、0、0,1、0、0、0、1、0、0,1,…である。 (となります(大日本印刷 A024362)。 4497>4x+1の形の最初の数個の素数は、5、13、17、29、37、41、53、61、73、89、97、101、109、113、137、……である。 (OEIS A002144)であるから、1、2、4、8、16、…の原始直角三角形の斜辺となる最小の辺の長さは5、65、1105、32045、1185665、48612265、…である。 (です(OEIS A006278)。
![]() を斜辺とする原始直角三角形または非原始直角三角形の可能な数は
を斜辺とする原始直角三角形または非原始直角三角形の可能な数は
|
(29)
|
|||
|
(30)
|
(Beiler 1966の誤記訂正)。 p. 117, which states that this formula gives the number of non-primitive solutions only), where ![]() is the sum of squares function.この式は非原始解の数を与えるとしている。 例えば、斜辺が65の整数の三角形は4つあり、
is the sum of squares function.この式は非原始解の数を与えるとしている。 例えば、斜辺が65の整数の三角形は4つあり、
|
(31)
|
![]() ,2,…の最初の数個は0,0,0,1,0,0,1,1,0,0,・・・です。 (OEIS A046080)。
,2,…の最初の数個は0,0,0,1,0,0,1,1,0,0,・・・です。 (OEIS A046080)。 ![]() 個の異なる三角形を持つ最小の斜辺は1, 5, 25, 125, 65, 3125, …である。 (OEIS A006339) である。 次の表は、
個の異なる三角形を持つ最小の斜辺は1, 5, 25, 125, 65, 3125, …である。 (OEIS A006339) である。 次の表は、![]() , 1, …, 5において、ちょうど
, 1, …, 5において、ちょうど![]() 個の異なる直交三角形が存在する斜辺を与える。
個の異なる直交三角形が存在する斜辺を与える。
| OEIS | 個の整数三角形が存在する斜辺 | |||
| 0 | A004144 | 1,2,3,4,6,7,8,9,11,12,14,16,18,……,1,2,4,6,8,9,12,16,18,……., | 2,2,3,4,……, | 1,2,3,4,……, |
| 1 | a084645 | 5, 10, 13, 15, 17, 20, 26, 29, 30, 34, 35, … | ||
| 2 | a084646 | 25、50、75、100、150、169、175、200、225、… …… | ||
| 3 | a084647 | |||
| 4 | a084648 | 65, 85, 130, 145, 170, 185, 195, 205, 221, 255, … | ||
| 5 | A084649 | 3125, 6250, 9375, 12500, 18750, 21875, 25000, … |
したがって、![]() が直角三角形の脚または斜辺になる方法の総数は
が直角三角形の脚または斜辺になる方法の総数は
| |
(32)
|
s=1,2,…の値は0,0,1,1,2,1,2,1,4,2,1,5,3,…であ る。 (となる(大日本印刷 A046081)。 2437>T=1<5097>、2、…のとき、<4585>個の一般直角三角形の辺となりうる最小の数<7343>は、3、5、16、12、15、125、24、40、…である。 (OEIS A006593; Beiler 1966, p.114)。
斜辺が100未満のピタゴラスの三角形は50個あり、![]() の大きい順に並べると、(3, 4, 5),(6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083、A046084、A009000)。
の大きい順に並べると、(3, 4, 5),(6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083、A046084、A009000)。
このうち、斜辺が100未満の原始3連は16個だけである。 (3, 4,5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65)、(16、63、65)、(48、55、73)、(36、77、85)、(13、84、85)、(39、80、89)、(65、72、97)(OEIS A046086、A046087、A020882)である。
斜辺が![]() の三角形の数を
の三角形の数を![]() 、斜辺が
、斜辺が![]() の三角形の数を
の三角形の数を![]() 、
、![]() 以下の原始三重項の数を
以下の原始三重項の数を![]() と表記する。 そして、10の累乗の値を以下の表にまとめる。
と表記する。 そして、10の累乗の値を以下の表にまとめる。
| OEIS | ||
| A101929 | 1, 50, 878, 12467, … | |
| A101930 | 2, 52, 881, 12471, ….… | |
| A101931 | 1, 16, 158, 1593, …。 |
Lehmer (1900) は斜辺が![]() より小さい原始解の数は
より小さい原始解の数は
|
(33)
|
(OEIS A086201).

最初のいくつかの原始ピタゴラストライアングルのインラディを増加 ![]() 順で並べて、1、2、3、6、5、4、10、5、・・で与えられます。 (OEIS A014498).
順で並べて、1、2、3、6、5、4、10、5、・・で与えられます。 (OEIS A014498).
面積の等しいピタゴラス三角形の三つ組を得る一般的な方法がある。 7670>
|
(34)
|
|||
|
(35)
|
|||
|
(36)
|
|||
|
(37)
|
|||
|
(38)
|
|||
|
(39)
|
次に、各三角形が生成する直角形(![]() ) は共通面積
) は共通面積
|
(40)
|
(Beiler 1966, pp.1). 126-127). この関数の唯一の極限は![]() で発生する。
で発生する。 ![]() に対して
に対して![]() なので、3つの非原始直角三角形が共有する最小面積は
なので、3つの非原始直角三角形が共有する最小面積は![]() で与えられ、その面積は840となり、3角形 (24, 70, 74), (40, 42, 58), (15, 112, 113) に対応する (Beiler 1966, p.126).
で与えられ、その面積は840となり、3角形 (24, 70, 74), (40, 42, 58), (15, 112, 113) に対応する (Beiler 1966, p.126).
面積が1桁の直角三角形には![]() (面積6)、
(面積6)、![]() (面積66666;Wells 1986, p. 89)
(面積66666;Wells 1986, p. 89)
1643年にFermatが、斜辺と足の合計が正方形のピタゴラスの三つ組を求める課題をメルセンヌに出した。 フェルマーはそのような最小の解を見つけた。
|
(41)
|
|||
|
(42)
|
|||
|
(43)
|
と
|
(44)
|
|||
|
(45)
|
関連する問題として、指定した整数![]() が有理辺の直角三角形の面積になるかどうかを判定する問題があります。 1、2、3、4は有理辺の直角三角形の面積ではないが、5は(3/2、20/3、41/6)であり、6(3、4、5)である。 この問題の解には楕円曲線
が有理辺の直角三角形の面積になるかどうかを判定する問題があります。 1、2、3、4は有理辺の直角三角形の面積ではないが、5は(3/2、20/3、41/6)であり、6(3、4、5)である。 この問題の解には楕円曲線
|
(46)
|
(46)に有理解があれば解(![]() ,
, ![]() ,
, ![]() )が存在します。 この場合
)が存在します。 この場合
|
(47)
|
|||
|
(48)
|
(Koblitz 1993)となる。 任意の![]() に対して解があるかどうかを判断する一般的な方法は知られていないが、1983年にJ. Tunnellが考案した手法により、ある値を除外することができる(Cipra 1996).
に対して解があるかどうかを判断する一般的な方法は知られていないが、1983年にJ. Tunnellが考案した手法により、ある値を除外することができる(Cipra 1996).
。