エンティティ間の重要性やパワー、影響力を探る科学者の関心が高まっている分野の1つがグラフ理論というものである。 グラフ理論のルーツは、1736 年に数学者カール・エーラーがレオンハルト・オイラーに「ケーニヒスベルクの橋」問題を紹介したときに始まります。 その中心部には2つの大きな島があり、互いに、また川岸とは7つの橋で結ばれていました。 カール・エーラーは、この7つの橋を2度以上渡らずに、それぞれの橋の中を歩くルートを見つけることに夢中になった。 そこでエーラーは、スイスの数学者オイラーに相談した。 オイラーは、この問題には解がないというエーラーの仮説を確認し、オイラーの説明は、「位置の幾何学」という新しい数学のパラダイムに影響を与えました。 その代わりに、それぞれの橋を点(ノード)とし、それらの間のリンクを表す線(エッジ)にすることで、問題を単純化することができるのである。 このノードとエッジを使用する方法は、現在ではグラフ理論として知られている。
Konigsberg の橋の問題については、こちらで詳しく説明している。 しかし、大規模な並べ換えを処理できる現代の計算能力により、グラフ理論の原理はより実用的なものとなっています。 この記事では、グラフ理論の原理を Python ベースの解析に応用する方法を学びます。


Graph システムにおけるすべてのネットワークは相互接続しているわけではないのです。 この断絶がコンポーネントを形成するときである。 下のグラフに示すように、コンポーネントはすべてのノードが他のノードへのパスを持っているときだけ形成されます。
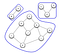
Applied Graph Theory in Python
Python において、ネットワーク解析ともよばれる応用グラフ理論には、しばしば networkx が使用されます。 このパッケージは、グラフの特徴を素早く要約するのに便利な機能を備えています。
まず、以下のコードでグラフの空白オブジェクトPを作成します。
<object>.nodes()や<object>.edges()などの引数は、グラフシステムのすべてのノードとエッジを表示する素早い方法です。
print(P.nodes())print(P.edges())
最後に、nx.drawはネットワークを視覚化するために使用されます。
%matplotlib inline
import matplotlib.pyplot as plt
nx.draw(P, with_labels = True)
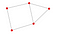
演習1:
さて、グラフの基本概念について述べたが、次の練習は良い方法だ:
- 上のグラフにはいくつノードがあるか?
- 上のグラフにある辺はいくつあるか?
- EとCの測地線は?
- グラフに1つ以上の成分があるか?
Using Real Data
以下の演習は2015年の米国内のフライトデータを使用します。 データセットには、出発地と目的地の空港に加え、飛行時間や遅延(天候、セキュリティ、航空会社関連)などのフライトを説明する属性が含まれています。
データセットが大きいため、演習ではロサンゼルス地域の空港(ロサンゼルス(LAX)、バーバンク(BUR)、オレンジ郡(SNA)、サンバーナーディノ郡(ONT))から出発するフライトに集中します。 さらに、日曜日を出発して木曜日に戻るという、デロイトの出張スケジュールに似たフライトを重点的に検討します。
出発地と目的地のデータがすでにあるため、***フィールド ORIGIN_AIRPORT と DESTINATION_AIRPORT はノードとエッジのソース フィールドとして機能し、最初の演習で行ったようにノードまたはエッジを作成する必要はありません。 ノードが定義されると、<object>.edges()はそれらの間のすべての対の関係を提供する。 最後に、nx.drawはエッジに対するグラフを生成するのに役立ちます。

FG.edges()

nx.draw(FG, with_labels = True)
上の出力において。 ノードは空港コードでラベル付けされている。 すべてのエッジは、ロサンゼルス地域の4つの空港のいずれかにつながっています。これは、この演習で選ばれたのがこの4つだけだったからです。 ロサンゼルス国際空港(LAX)は、4つの空港の中で最大の空港であり、グラフは、多くの都市がLAXにしかアクセスできず、他の小さな空港からはアクセスできないことを明確に示しています。 これは、LAXの連結性(度数中心性)を示している。 networkx では、グラフ システムの各ノードの中心度を求めるために、nx.algorithms.degree_centrality(<object>) **** が使用されます。
# Calculating the centrality of each of the airports
nx.algorithms.degree_centrality(FG)
さらに細かく、短い「for ループ」を使用して、関心のある 2 つの領域間のエッジを生成することが可能です。 たとえば、次のコードは、日曜日または木曜日のいずれかにサンバーナーディーノ郡 (ONT) からニューアーク (EWR) まで可能なすべてのフライトを見つけるために使用します。
San Bernardino County と Newark 間のいくつかのフライト オプションの中から、nx.dijkstra_path を使用してユークリッド パス (または最短経路) を見つけることができます。
#Finding the dijkstra path
djk_path = nx.dijkstra_path(FG, source='ONT', target='EWR')
djk_path
演習 2:
nx.draw()を用いて次のグラフを生成してください。 注意:あなたのネットワークは全く同じには見えないかもしれませんが、パス、エッジ、ノードは以下のネットワークと一致するはずです。- すべてのエッジをプリントアウトしてください。

からどのパスが最も短いですか?