Less…
Una tripla pitagorica è una tripla di numeri interi positivi 
, 
, e 
tale che esiste un triangolo rettangolo con gambe 
e ipotenusa 
. Per il teorema di Pitagora, questo equivale a trovare gli interi positivi 
, 
, e 
che soddisfano
 |
(1)
|
Il più piccolo e noto triplo pitagorico è 
. Il triangolo rettangolo che ha queste lunghezze laterali è talvolta chiamato triangolo 3, 4, 5.
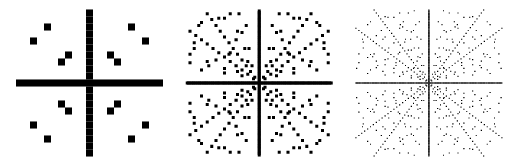
I tracciati dei punti nel piano 
tali che 
sia una tripla pitagorica sono mostrati sopra per limiti successivamente più grandi. Questi grafici includono valori negativi di 
e 
, e sono quindi simmetrici su entrambi gli assi x e y.
Similmente, i grafici dei punti nel piano 
tali che 
è una tripla pitagorica sono mostrati sopra per limiti successivamente maggiori.
Si usa considerare solo le triple pitagoriche primitive (dette anche “ridotte”) in cui 
e 
sono relativamente primi, poiché altre soluzioni possono essere generate banalmente da quelle primitive. Le triple primitive sono illustrate sopra, e si può vedere immediatamente che le linee radiali corrispondenti alle triple imprimitive nel grafico originale sono assenti in questa figura. Per le soluzioni primitive, una di 
o 
deve essere pari, e l’altra dispari (Shanks 1993, p. 141), con 
sempre dispari.
Inoltre, un lato di ogni tripla pitagorica è divisibile per 3, un altro per 4, e un altro per 5. Un lato può avere due di questi divisori, come in (8, 15, 17), (7, 24, 25), e (20, 21, 29), o anche tutti e tre, come in (11, 60, 61).
Data una tripla primitiva 
, tre nuove triple primitive si ottengono da
 |
 |
 |
(2)
|
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
dove
 |
 |
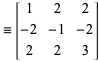(5)
|
 |
 |
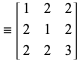(6)
|
 |
 |
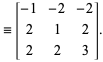(7)
|
Hall (1970) e Roberts (1977) dimostrano che 
è una tripla pitagorica primitiva iff
 |
(8)
|
dove 
è un prodotto finito delle matrici 
, 
, 
. Ne segue quindi che ogni tripla pitagorica primitiva deve essere un membro della matrice infinita
 |
(9)
|
Pythagoras e i Babilonesi diedero una formula per generare triple (non necessariamente primitive) come
 |
(10)
|
per 
, che genera un insieme di triple distinte che non contiene né tutte le primitive né tutte le imprimitive (e dove nel caso speciale 
, 
).
I primi greci davano
 |
(11)
|
dove 
e 
sono relativamente primi e di parità opposta (Shanks 1993, p. 141), che genera un insieme di triple distinte contenenti precisamente le triple primitive (dopo aver opportunamente ordinato 
e 
).
Lasciamo che 
sia un numero di Fibonacci. Allora
 |
(12)
|
genera distinte triple pitagoriche (Dujella 1995), sebbene non in modo esaustivo né per le triple primitive né per quelle imprimitive. Più in generale, partendo dagli interi positivi 
, 
, e costruendo la sequenza di Fibonacci 
con termini 
, 
, 
, 
, 
, … genera distinte triple pitagoriche
 |
(13)
|
(Horadam 1961), dove
 |
(24)
|
(Beiler 1966, p. 116). Si noti che 
se 
è primo o due volte primo. I primi numeri per 
, 2, … sono 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 4, 1, … (OEIS A046079).
Per trovare il numero di modi in cui 
un numero 
può essere l’ipotenusa di un triangolo rettangolo primitivo, scrivere la sua fattorizzazione come
 |
(25)
|
dove le 
s sono della forma 
e le 
sono della forma 
. Il numero di possibili triangoli rettangoli primitivi è quindi
 |
(26)
|
Per esempio, 
poiché
 |
 |
 |
(27)
|
 |
 |
 |
(28)
|
I valori di 
per 
, 2, … sono 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, … (OEIS A024362). I primi primati della forma 
sono 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, … (OEIS A002144), quindi le più piccole lunghezze dei lati che sono le ipotenuse di 1, 2, 4, 8, 16, … triangoli rettangoli primitivi sono 5, 65, 1105, 32045, 1185665, 48612265, … (OEIS A006278).
Il numero di possibili triangoli rettangoli primitivi o non primitivi aventi 
come ipotenusa è
 |
 |
 |
(29)
|
 |
 |
 |
(30)
|
(correzione del refuso di Beiler 1966, p. 117, che afferma che questa formula dà solo il numero di soluzioni non primitive), dove 
è la funzione somma dei quadrati. Per esempio, ci sono quattro distinti triangoli interi con ipotenusa 65, poiché
 |
(31)
|
I primi numeri per 
, 2, … sono 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, … (OEIS A046080). Le ipotene più piccole che hanno 
tripli distinti sono 1, 5, 25, 125, 65, 3125, … (OEIS A006339). La seguente tabella fornisce le ipotenuse per le quali esistono esattamente 
triangoli interi retti distinti per 
, 1, …, 5.
 |
OEIS | ipoteni per i quali esistono  distinti triangoli interi |
| 0 | A004144 | 1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, … |
| 1 | A084645 | 5, 10, 13, 15, 17, 20, 26, 29, 30, 34, 35, … |
| 2 | A084646 | 25, 50, 75, 100, 150, 169, 175, 200, 225, … |
| 3 | A084647 | 125, 250, 375, 500, 750, 875, 1000, 1125, 1375, … |
| 4 | A084648 | 65, 85, 130, 145, 170, 185, 195, 205, 221, 255, … |
| 5 | A084649 | 3125, 6250, 9375, 12500, 18750, 21875, 25000, … |
Quindi, il numero totale di modi in cui 
può essere sia una gamba che l’ipotenusa di un triangolo rettangolo è dato da
 |
(32)
|
I valori per 
, 2, … sono 0, 0, 1, 1, 2, 1, 1, 2, 2, 2, 2, 1, 4, 2, 1, 5, 3, … (OEIS A046081). I più piccoli numeri 
che possono essere i lati di 
triangoli rettangoli generali per 
, 2, … sono 3, 5, 16, 12, 15, 125, 24, 40, … (OEIS A006593; Beiler 1966, p. 114).
Ci sono 50 triple pitagoriche con ipotenusa inferiore a 100, le prime delle quali, ordinate per incremento 
, sono (3, 4, 5), (6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083, A046084 e A009000).
Di queste, solo 16 sono terzine primitive con ipotenusa inferiore a 100: (3, 4,5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65), (16, 63, 65), (48, 55, 73), (36, 77, 85), (13, 84, 85), (39, 80, 89), e (65, 72, 97) (OEIS A046086, A046087, e A020882).
Lasciamo che il numero di triple con ipotenusa 
sia denominato 
, il numero di triple con ipotenusa 
sia denominato 
, e il numero di triple primitive inferiori a 
sia denominato 
. Poi la seguente tabella riassume i valori per potenze di 10.
 |
OEIS |  ,  , … |
 |
A101929 | 1, 50, 878, 12467, … |
 |
A101930 | 2, 52, 881, 12471, … |
 |
A101931 | 1, 16, 158, 1593, … |
Lehmer (1900) dimostrò che il numero di soluzioni primitive con ipotenusa minore di 
soddisfa
 |
(33)
|
(OEIS A086201).
Gli inradii dei primi pochi triangoli pitagorici primitivi ordinati per incremento 
sono dati da 1, 2, 3, 3, 6, 5, 4, 10, 5, … (OEIS A014498).
C’è un metodo generale per ottenere terzine di triangoli pitagorici con aree uguali. Prendiamo i tre insiemi di generatori come
 |
 |
 |
(34)
|
 |
 |
 |
(35)
|
 |
 |
 |
(36)
|
 |
 |
 |
(37)
|
 |
 |
 |
(38)
|
 |
 |
 |
(39)
|
Quindi il triangolo rettangolo generato da ogni tripla (
) ha area comune
 |
(40)
|
(Beiler 1966, pp. 126-127). L’unico estremo di questa funzione si trova a 
. Poiché 
per 
, la più piccola area condivisa da tre triangoli rettangoli non primitivi è data da 
, che risulta in un’area di 840 e corrisponde alle terzine (24, 70, 74), (40, 42, 58) e (15, 112, 113) (Beiler 1966, p. 126).
Triangoli retti le cui aree consistono in una sola cifra includono 
(area di 6) e 
(area di 666666; Wells 1986, p. 89).
Nel 1643, Fermat sfidò Mersenne a trovare una terzina pitagorica la cui ipotenusa e somma delle gambe fossero quadrati. Fermat trovò la più piccola soluzione di questo tipo:
 |
 |
 |
(41)
|
 |
 |
 |
(42)
|
 |
 |
 |
(43)
|
con
 |
 |
 |
(44)
|
 |
 |
 |
(45)
|
Un problema correlato è determinare se un intero specificato 
può essere l’area di un triangolo rettangolo con lati razionali. 1, 2, 3 e 4 non sono le aree di nessun triangolo rettangolo con lati razionali, ma 5 lo è (3/2, 20/3, 41/6), così come 6 (3, 4, 5). La soluzione del problema coinvolge la curva ellittica
 |
(46)
|
Una soluzione (
, 
, 
) esiste se (46) ha una soluzione razionale, nel qual caso
 |
 |
 |
(47)
|
 |
 |
 |
(48)
|
(Koblitz 1993). Non esiste un metodo generale conosciuto per determinare se esiste una soluzione per 
arbitrari, ma una tecnica ideata da J. Tunnell nel 1983 permette di escludere certi valori (Cipra 1996).