Una crescente area di interesse per gli scienziati che esplorano l’importanza, il potere o l’influenza tra entità è chiamata Teoria dei Grafi. Le radici della teoria dei grafi iniziarono nel 1736 quando il matematico Carl Ehler presentò a Leonhard Euler il problema dei ponti di Konigsberg.
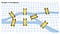
Il problema dei ponti di Konigsberg si basa sull’ex città tedesca di Konigsberg che si trova su entrambi i lati del fiume Pregel. Nel centro, c’erano due grandi isole che erano collegate tra loro e alle rive del fiume da sette ponti. Carl Ehler divenne ossessionato dal trovare un percorso per camminare attraverso ognuno dei sette ponti senza camminare su nessuno di essi più di una volta. Ehler contattò Leonhard Euler, un matematico svizzero. Euler confermò l’ipotesi di Ehler che il problema non aveva una soluzione, e la spiegazione di Euler informò un nuovo paradigma matematico chiamato Geometria della posizione.
Il nuovo paradigma geometrico di Euler affermava che la posizione dei ponti non aveva importanza. Il problema, invece, può essere semplificato trasformando ogni ponte in un punto (nodo) con linee (bordi) per rappresentare i collegamenti tra di loro. Questa pratica di usare nodi e spigoli è ora conosciuta come Teoria dei Grafi.
Puoi leggere di più sul problema dei ponti di Konigsberg qui.
Inizialmente, la Teoria dei Grafi non serviva a molto nella risoluzione dei problemi e non era molto considerata dai matematici. Tuttavia, la moderna potenza di calcolo per elaborare grandi permutazioni ha reso i principi della teoria dei grafi più pratici. Questo articolo ti insegna ad applicare i principi della Teoria dei Grafi all’analisi basata su Python.


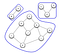
Non tutte le reti in un sistema Graph sono interconnesse. Questa disconnessione avviene quando si formano i componenti. Come mostrato nel grafico qui sotto, un componente è formato solo quando ogni nodo ha un percorso verso altri nodi.
Teoria dei grafi applicata in Python
In Python, networkx è spesso usato per la teoria dei grafi applicata, nota anche come analisi delle reti. Il pacchetto ha funzionalità utili per riassumere rapidamente le caratteristiche di un grafico. Potete rivedere i passi qui sotto e seguirli mentre creiamo un grafo e ne comprendiamo la composizione.
Prima il codice qui sotto crea un oggetto grafico vuoto P. I passi successivi aggiungono i nodi e descrivono i bordi.
Argomenti come <object>.nodes() o <object>.edges() sono modi rapidi per visualizzare tutti i nodi e i bordi del sistema di grafi.
print(P.nodes())print(P.edges())
Infine, nx.draw è usato per visualizzare la rete.
%matplotlib inline
import matplotlib.pyplot as plt
nx.draw(P, with_labels = True)
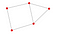
Esercizi 1:
Ora che i concetti di base dei grafi sono stati discussi, i seguenti esercizi sono un buon metodo per fare pratica:
- Quanti nodi ci sono nel grafico sopra?
- Quanti bordi ci sono nel grafico di sopra?
- Qual è la geodetica per E e C?
- Ci sono più di 1 componente nel grafico?
Utilizzando dati reali
L’esercizio seguente userà i dati per i voli negli Stati Uniti nel 2015. Il set di dati include gli aeroporti di origine e di destinazione, oltre agli attributi che descrivono il volo, tra cui la durata del volo e i ritardi (legati al tempo, alla sicurezza o alla compagnia aerea).
Perché il set di dati è grande, l’esercizio si concentrerà sui voli che hanno origine dagli aeroporti della zona di Los Angeles (Los Angeles (LAX), Burbank (BUR), Orange County (SNA), e San Bernardino County (ONT)). Inoltre, l’obiettivo sarà quello di esaminare i voli che assomigliano al mio programma di viaggio Deloitte – volando fuori la domenica e tornando il giovedì.
Siccome abbiamo già i dati di origine e destinazione, ****fields ORIGIN_AIRPORT e DESTINATION_AIRPORT serviranno come campi sorgente per nodi e bordi – non è necessario creare nodi o bordi come abbiamo fatto nel primo esercizio. Una volta che i nodi sono definiti, <object>.edges() fornirà tutte le relazioni di coppia tra loro. Infine, nx.draw aiuterà a produrre un grafico dei bordi.

FG.edges()

nx.draw(FG, with_labels = True)

Nell’output precedente, i nodi sono etichettati con i codici degli aeroporti. Tutti i bordi portano a uno dei quattro aeroporti dell’area di Los Angeles perché questi quattro erano gli unici selezionati per questo esercizio. Los Angeles International (LAX) è l’aeroporto più grande tra i quattro e il grafico mostra chiaramente che molte città sono accessibili solo da LAX e non da altri aeroporti più piccoli. Questo mostra la connessione, o grado di centralità, di LAX. In networkx, nx.algorithms.degree_centrality(<object>) ****è usato per trovare la centralità di ogni nodo nel sistema del grafico.
# Calculating the centrality of each of the airports
nx.algorithms.degree_centrality(FG)
Possiamo andare più in profondità e usare un breve ‘ciclo for’ per produrre bordi tra due aree di interesse. Per esempio, il seguente codice è usato per trovare tutti i possibili voli da San Bernardino County (ONT) a Newark (EWR) la domenica o il giovedì.
Tra le varie opzioni di volo tra San Bernardino County e Newark, il nx.dijkstra_path può essere usato per trovare il percorso euclideo (o il percorso più breve).
#Finding the dijkstra path
djk_path = nx.dijkstra_path(FG, source='ONT', target='EWR')
djk_path
Esercizi 2:
- Produci il seguente grafico usando
nx.draw(). Nota: la tua rete potrebbe non avere esattamente lo stesso aspetto, ma i percorsi, i bordi e i nodi dovrebbero corrispondere alla rete sottostante. - Stampa tutti i bordi.
- Qual è il percorso più breve da L a F?
