Più del 90% dei solidi naturali e artificiali sono cristallini.spiegare l’uso delle misure di diffrazione dei raggi X per determinare le strutture cristalline

Oltre il 90% dei solidi naturali e di quelli prodotti dall’uomo sono cristallini. La maggior parte dei solidi si formano con una disposizione regolare delle loro particelle perché le interazioni attrattive complessive tra le particelle sono massimizzate, e l’energia intermolecolare totale è minimizzata, quando le particelle si imballano nel modo più efficiente. La disposizione regolare a livello atomico si riflette spesso a livello macroscopico. In questo modulo, esploreremo alcuni dettagli sulle strutture dei solidi cristallini metallici e ionici, e impareremo come queste strutture sono determinate sperimentalmente.

Le strutture dei metalli

Inizieremo la nostra discussione sui solidi cristallini considerando i metalli elementari, che sono relativamente semplici perché ognuno contiene solo un tipo di atomo. Un metallo puro è un solido cristallino con atomi di metallo impacchettati strettamente insieme in un modello che si ripete. Alcune delle proprietà dei metalli in generale, come la loro malleabilità e duttilità, sono in gran parte dovute all’avere atomi identici disposti in uno schema regolare. Le diverse proprietà di un metallo rispetto ad un altro dipendono in parte dalle dimensioni dei loro atomi e dalle specifiche delle loro disposizioni spaziali. Esploreremo le somiglianze e le differenze di quattro delle più comuni geometrie cristalline dei metalli nelle sezioni che seguono.

Celle unitarie dei metalli

La struttura di un solido cristallino, sia esso un metallo o meno, è meglio descritta considerando la sua unità ripetuta più semplice, che viene chiamata cella unitaria. La cella unitaria consiste di punti di reticolo che rappresentano le posizioni degli atomi o degli ioni. L’intera struttura consiste quindi in questa cella unitaria che si ripete in tre dimensioni, come illustrato nella figura 1.

Figura 1. Una cella unitaria mostra le posizioni dei punti del reticolo che si ripetono in tutte le direzioni.

Cominciamo la nostra indagine sulla struttura del reticolo cristallino e sulle celle unitarie con la struttura più semplice e la cella unitaria più elementare. Per visualizzarla, immaginate di prendere un gran numero di sfere identiche, come le palle da tennis, e di disporle uniformemente in un contenitore. Il modo più semplice per farlo sarebbe quello di fare degli strati in cui le sfere in uno strato sono direttamente sopra quelle nello strato sottostante, come illustrato nella figura 2. Questa disposizione è chiamata struttura cubica semplice, e la cella unitaria è chiamata cella cubica semplice o cella cubica primitiva.

Figura 2. Quando gli atomi di metallo sono disposti con sfere in uno strato direttamente sopra o sotto sfere in un altro strato, la struttura del reticolo è chiamata cubica semplice. Si noti che le sfere sono in contatto.

In una struttura cubica semplice, le sfere non sono imballate così strettamente come potrebbero essere, e “riempiono” solo circa il 52% del volume del contenitore. Questa è una disposizione relativamente inefficiente, e solo un metallo (polonio, Po) cristallizza in una struttura cubica semplice. Come mostrato nella figura 3, un solido con questo tipo di disposizione consiste di piani (o strati) in cui ogni atomo contatta solo i quattro vicini più vicini nel suo strato; un atomo direttamente sopra di esso nello strato superiore; e un atomo direttamente sotto di esso nello strato inferiore. Il numero di altre particelle che ogni particella in un solido cristallino contatta è noto come il suo numero di coordinazione. Per un atomo di polonio in una semplice matrice cubica, il numero di coordinazione è quindi sei.

Figura 3. Un atomo in una struttura a reticolo cubico semplice entra in contatto con altri sei atomi, quindi ha un numero di coordinazione di sei.

In un reticolo cubico semplice, la cella unitaria che si ripete in tutte le direzioni è un cubo definito dai centri di otto atomi, come mostrato nella figura 4. Gli atomi agli angoli adiacenti di questa cella unitaria sono in contatto tra loro, quindi la lunghezza del bordo di questa cella è uguale a due raggi atomici, o un diametro atomico. Una cella unitaria cubica contiene solo le parti di questi atomi che si trovano al suo interno. Poiché un atomo in un angolo di una cella cubica semplice è contenuto da un totale di otto celle unitarie, solo un ottavo di quell’atomo è all’interno di una specifica cella unitaria. E poiché ogni cella cubica semplice ha un atomo in ognuno dei suoi otto “angoli”, c’è 8 volte \frac{1}{8}=1 atomo dentro una cella cubica semplice.

Figura 4. Una semplice cella unitaria del reticolo cubico contiene un ottavo di atomo in ognuno dei suoi otto angoli, quindi contiene un atomo in totale.

Esempio 1: Calcolo del raggio atomico e della densità per i metalli, parte 1

La lunghezza del bordo della cella unitaria del polonio alfa è 336 pm.

1. Determina il raggio di un atomo di polonio.
2. Determina la densità del polonio alfa.

Mostra la soluzione

Il polonio alfa cristallizza in una cella unitaria cubica semplice:

1. Due atomi di Po adiacenti sono in contatto tra loro, quindi la lunghezza del bordo di questa cella è uguale a due raggi atomici di Po: l=2r. Quindi, il raggio di Po è r===dfrac{l}}{2}===dfrac{336 pm}{2}={168 pm}.
2. La densità è data da \testo{densità}==dfrac{massa}{{testo{volume}}. La densità del polonio può essere trovata determinando la densità della sua cella unitaria (la massa contenuta in una cella unitaria divisa per il volume della cella unitaria). Poiché una cella unitaria Po contiene un ottavo di un atomo Po in ciascuno dei suoi otto angoli, una cella unitaria contiene un atomo Po.

La massa di una cella unitaria Po può essere trovata da:

Testo di una cella unitaria Po} †dfrac{1 atomo Po} †dfrac{1 mol Po} †6.022 volte {10}^{23} atomi di Po} {ddfrac{208.998{text{g}{1 mol Po}=3.47 volte {10}^{22}{text{g}

Il volume di una cella unitaria di Po può essere trovato da:

V={l}^{3}=(336 volte {10}^{-10}{text{cm})}^{3}=3.79 volte {10}^{-23}{{text{cm}}^{3}

(Si noti che la lunghezza del bordo è stata convertita da pm a cm per ottenere le solite unità di volume per la densità.)

Quindi, la densità di \text{Po}=\dfrac{3.471 volte {10}^{-22}{testo{g}{3,79 volte {10}^{-23}{testo{cm}}^{3}}={9,16 g/cm}^{3}

Controlla il tuo apprendimento

La lunghezza del bordo della cella unitaria del nichel è 0,3524 nm. La densità del Ni è 8,90 g/cm3. Il nichel cristallizza in una struttura cubica semplice? Spiega.

Mostra la soluzione

No. Se il Ni fosse cubico semplice, la sua densità sarebbe data da:

{1 atomo di Ni}times \dfrac{1 mol Ni}{6.022 volte {10}^{23} di atomi di Ni}} ¼ volte \dfrac{58.693{text{g}}=9.746 volte {10}^{-23} di Ni}
V={l}^{3}=(3.524 volte {10}^{-8}{text{cm})}^{3}=4.376 volte {10}^{-23}{{text{cm}}^{3}

Allora la densità del Ni sarebbe ==dfrac{9,746 volte {10}^{-23}{text{g}}{4,376 volte {10}^{-23}{{cm}^{3}}={2.23 g/cm}^{3}

Siccome la densità reale del Ni non è vicina a questa, il Ni non forma una struttura cubica semplice.

La maggior parte dei cristalli di metallo sono uno dei quattro principali tipi di cellule unitarie. Per ora, ci concentreremo sulle tre cellule cubiche: cubica semplice (che abbiamo già visto), cubica centrata sul corpo e cubica centrata sulla faccia, tutte illustrate nella figura 5. (Si noti che ci sono in realtà sette diversi sistemi di reticolo, alcuni dei quali hanno più di un tipo di reticolo, per un totale di 14 diversi tipi di cellule. Lasciamo le geometrie più complicate per più avanti in questo modulo.)

Figura 5. Le celle unitarie cubiche dei metalli mostrano (nelle figure superiori) le posizioni dei punti di reticolo e (nelle figure inferiori) gli atomi di metallo situati nella cella unitaria.

Alcuni metalli cristallizzano in una disposizione che ha una cella unitaria cubica con atomi in tutti gli angoli e un atomo al centro, come mostrato nella figura 6. Questo è chiamato un cubo centrato sul corpo. Questo è chiamato un solido cubico centrato sul corpo (BCC). Gli atomi negli angoli di una cella unitaria BCC non entrano in contatto tra loro, ma con l’atomo al centro. Una cella unitaria BCC contiene due atomi: un ottavo di un atomo in ognuno degli otto angoli (8 volte \frac{1}{8}=1 atomo dagli angoli) più un atomo dal centro. Ogni atomo in questa struttura tocca quattro atomi nello strato superiore e quattro atomi nello strato inferiore. Così, un atomo in una struttura BCC ha un numero di coordinazione di otto.

Figura 6. In una struttura cubica centrata sul corpo, gli atomi in uno specifico strato non si toccano tra loro. Ogni atomo tocca quattro atomi nello strato sovrastante e quattro atomi nello strato sottostante.

Gli atomi nelle disposizioni BCC sono molto più efficientemente imballati che in una struttura cubica semplice, occupando circa il 68% del volume totale. I metalli isomorfi con una struttura BCC includono K, Ba, Cr, Mo, W e Fe a temperatura ambiente. (Elementi o composti che cristallizzano con la stessa struttura sono detti isomorfi.)

Molti altri metalli, come alluminio, rame e piombo, cristallizzano in una disposizione che ha una cella unitaria cubica con atomi in tutti gli angoli e nei centri di ogni faccia, come illustrato nella figura 7. Questa disposizione è chiamata un solido cubico a facce centrate (FCC). Una cella unitaria FCC contiene quattro atomi: un ottavo di un atomo a ciascuno degli otto angoli (8 volte \frac{1}{8}=1 atomo dagli angoli) e la metà di un atomo su ciascuna delle sei facce (6 volte \frac{1}{2}=3 atomi dalle facce). Gli atomi agli angoli toccano gli atomi nei centri delle facce adiacenti lungo le diagonali delle facce del cubo. Poiché gli atomi sono su punti identici del reticolo, hanno ambienti identici.

Figura 7. Un solido cubico a facce centrate ha gli atomi agli angoli e, come dice il nome, ai centri delle facce delle sue celle unitarie.

Gli atomi in una disposizione FCC sono impacchettati il più strettamente possibile, con gli atomi che occupano il 74% del volume. Questa struttura è anche chiamata imballaggio cubico più vicino (CCP). In CCP, ci sono tre strati ripetuti di atomi disposti esagonalmente. Ogni atomo tocca sei atomi nel proprio strato, tre nello strato superiore e tre nello strato inferiore. In questa disposizione, ogni atomo tocca 12 vicini, e quindi ha un numero di coordinazione di 12. Il fatto che le disposizioni FCC e CCP siano equivalenti può non essere immediatamente ovvio, ma il motivo per cui sono effettivamente la stessa struttura è illustrato nella figura 8.

Figura 8. Una disposizione CCP consiste in tre strati ripetuti (ABCABC…) di atomi disposti esagonalmente. Gli atomi in una struttura CCP hanno un numero di coordinazione di 12 perché contattano sei atomi nel loro strato, più tre atomi nello strato superiore e tre atomi nello strato inferiore. Ruotando la nostra prospettiva, possiamo vedere che una struttura CCP ha una cella unitaria con una faccia che contiene un atomo dello strato A in un angolo, atomi dello strato B attraverso una diagonale (a due angoli e al centro della faccia), e un atomo dello strato C nell’angolo rimanente. Questo è lo stesso di una disposizione cubica a facce centrate.

Perché l’imballaggio più stretto massimizza le attrazioni complessive tra gli atomi e minimizza l’energia intermolecolare totale, gli atomi nella maggior parte dei metalli si imballano in questo modo. Troviamo due tipi di impacchettamento più stretto nelle strutture cristalline metalliche semplici: CCP, che abbiamo già incontrato, e l’impacchettamento più vicino esagonale (HCP) mostrato nella figura 9. Entrambi consistono in strati ripetuti di atomi disposti esagonalmente. In entrambi i tipi, un secondo strato (B) è posto sul primo strato (A) in modo che ogni atomo del secondo strato sia in contatto con tre atomi del primo strato. Il terzo strato è posizionato in uno dei due modi. In HCP, gli atomi nel terzo strato sono direttamente sopra gli atomi nel primo strato (cioè, il terzo strato è anche di tipo A), e l’impilamento consiste in strati alternati di tipo A e di tipo B a pacchi ravvicinati (cioè, ABABAB⋯). In CCP, gli atomi nel terzo strato non sono sopra gli atomi in nessuno dei primi due strati (cioè, il terzo strato è di tipo C), e l’impilamento consiste in strati alternati di tipo A, tipo B, e tipo C impacchettati strettamente (cioè, ABCABCABC⋯). Circa due terzi di tutti i metalli cristallizzano in matrici impacchettate più vicine con numeri di coordinazione di 12. I metalli che cristallizzano in una struttura HCP includono Cd, Co, Li, Mg, Na, e Zn, e i metalli che cristallizzano in una struttura CCP includono Ag, Al, Ca, Cu, Ni, Pb, e Pt.

Figura 9. In entrambi i tipi di imballaggio più vicino, gli atomi sono imballati nel modo più compatto possibile. Il closest packing esagonale consiste in due strati alternati (ABABAB…). L’impacchettamento più vicino cubico consiste di tre strati alternati (ABCABCABC…).

Esempio 2: Calcolo del raggio atomico e della densità per i metalli, parte 2

Il calcio cristallizza in una struttura cubica faccia-centrata. La lunghezza del bordo della sua cella unitaria è 558.8 pm.

1. Qual è il raggio atomico di Ca in questa struttura?
2. Calcolare la densità di Ca.

Mostrare la soluzione

Parte 1

In una struttura FCC, gli atomi di Ca sono in contatto tra loro attraverso la diagonale della faccia, quindi la lunghezza della diagonale è uguale a quattro raggi atomici di Ca (d = 4r). Due spigoli adiacenti e la diagonale della faccia formano un triangolo rettangolo, con la lunghezza di ogni lato uguale a 558,8 pm e la lunghezza dell’ipotenusa uguale a quattro raggi atomici di Ca:

{{text{a}}^{2}+{{text{a}}^{2}={{text{d}}^{2}{longrightarrow {(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}={(4r)}^{2}

Solving this gives r=\sqrt{\dfrac{{(558.8\text{pm})}^{2}+{(558.5{text{pm})}^{2}}{16}={197.6 pmg per un raggio di Ca}.

Parte 2

La densità è data da \text{densità}={dfrac{{massa}{testo{volume}. La densità del calcio può essere trovata determinando la densità della sua cella unitaria: per esempio, la massa contenuta in una cella unitaria divisa per il volume della cella unitaria. Una cella unitaria di Ca a facce centrate ha un ottavo di un atomo in ognuno degli otto angoli \sinistra (8 volte \dfrac{1}{8}=1 atomo di testo}destra) e metà di un atomo su ognuna delle sei facce \sinistra (6 volte \dfrac{1}{2}=3 atomi di testo}destra), per un totale di quattro atomi nella cella unitaria.

La massa della cella unitaria può essere trovata da:

{1 cella unitaria di Ca}}times dfrac{4 atomi di Ca}{1 cella unitaria di Ca}}times dfrac{1 mol Ca}{6.022 volte {10}^{23}{testo{atomi di Ca}{tempi dfrac{40,078{testo{g}{testo{1 mol Ca}}=2.662 volte {10}^{-22}{text{g}

Il volume di una cella unitaria di Ca può essere trovato da:

V={a}^{3}=(558.8 volte {10}^{-10}{text{cm})}^{3}=1.745 volte {10}^{-22}{{text{cm}}^{3}

(Si noti che la lunghezza del bordo è stata convertita da pm a cm per ottenere le solite unità di volume per la densità.)

Allora, la densità di \testo{Ca}==dfrac{2,662 volte {10}^{-22}{testo{g}}{1,745 volte {10}^{-22}{testo{cm}^{3}}={1.53 g/cm}^{3}

Controlla il tuo apprendimento

L’argento cristallizza in una struttura FCC. La lunghezza del bordo della sua cella unitaria è 409 pm.

1. Qual è il raggio atomico di Ag in questa struttura?
2. Calcolare la densità di Ag.

Mostra Soluzioni

1. 144 pm
2. 10.5 g/cm3

In generale, una cella unitaria è definita dalle lunghezze di tre assi (a, b, e c) e dagli angoli (α, β, e γ) tra loro, come illustrato nella figura 10. Gli assi sono definiti come le lunghezze tra i punti del reticolo spaziale. Di conseguenza, gli assi delle celle unitarie uniscono punti con ambienti identici.

Figura 10. Una cella unitaria è definita dalle lunghezze dei suoi tre assi (a, b, e c) e dagli angoli (α, β, e γ) tra gli assi.

Ci sono sette diversi sistemi reticolari, alcuni dei quali hanno più di un tipo di reticolo, per un totale di quattordici diverse celle unitarie, che hanno le forme mostrate nella Figura 11.

Figura 11. Ci sono sette diversi sistemi di reticolo e 14 diverse celle unitarie.

Le strutture dei cristalli ionici

I cristalli ionici consistono di due o più tipi diversi di ioni che solitamente hanno dimensioni diverse. L’impacchettamento di questi ioni in una struttura cristallina è più complesso dell’impacchettamento di atomi metallici della stessa dimensione.

La maggior parte degli ioni monoatomici si comportano come sfere cariche, e la loro attrazione per ioni di carica opposta è la stessa in ogni direzione. Di conseguenza, le strutture stabili dei composti ionici risultano (1) quando gli ioni di una carica sono circondati dal maggior numero possibile di ioni di carica opposta e (2) quando i cationi e gli anioni sono in contatto tra loro. Le strutture sono determinate da due fattori principali: le dimensioni relative degli ioni e il rapporto tra il numero di ioni positivi e negativi nel composto.

Figura 12. I cationi possono occupare due tipi di buchi tra gli anioni: buchi ottaedrici o tetraedrici.

Nelle strutture ioniche semplici, di solito troviamo gli anioni, che sono normalmente più grandi dei cationi, disposti in una matrice più vicina. (Come visto in precedenza, elettroni addizionali attratti dallo stesso nucleo rendono gli anioni più grandi e meno elettroni attratti dallo stesso nucleo rendono i cationi più piccoli rispetto agli atomi da cui sono formati). I cationi più piccoli occupano comunemente uno dei due tipi di buchi (o interstizi) che rimangono tra gli anioni. Il più piccolo dei buchi si trova tra tre anioni in un piano e un anione in un piano adiacente. I quattro anioni che circondano questo buco sono disposti agli angoli di un tetraedro, quindi il buco è chiamato buco tetraedrico. Il tipo più grande di buco si trova al centro di sei anioni (tre in uno strato e tre in uno strato adiacente) situati agli angoli di un ottaedro; questo è chiamato un buco ottaedrico. La figura 12 illustra entrambi questi tipi di fori.

A seconda delle dimensioni relative dei cationi e degli anioni, i cationi di un composto ionico possono occupare fori tetraedrici o ottaedrici, come illustrato nella figura 13. I cationi relativamente piccoli occupano i fori tetraedrici e i cationi più grandi occupano i fori ottaedrici. Se i cationi sono troppo grandi per entrare nei fori ottaedrici, gli anioni possono adottare una struttura più aperta, come una semplice matrice cubica. I cationi più grandi possono quindi occupare i fori cubici più grandi resi possibili dalla spaziatura più aperta.

Figura 13. Le dimensioni di un catione e la forma del foro occupato dal composto sono direttamente correlate.

Ci sono due fori tetraedrici per ogni anione in una serie di anioni HCP o CCP. Un composto che cristallizza in una matrice di anioni con i cationi nei fori tetraedrici può avere un rapporto massimo cationi:anioni di 2:1; tutti i fori tetraedrici sono riempiti in questo rapporto. Gli esempi includono Li2O, Na2O, Li2S e Na2S. I composti con un rapporto inferiore a 2:1 possono anche cristallizzare in una matrice impacchettata più vicina di anioni con cationi nei fori tetraedrici, se le dimensioni ioniche si adattano. In questi composti, tuttavia, alcuni dei fori tetraedrici rimangono liberi.

Il rapporto tra fori ottaedrici e anioni in una struttura HCP o CCP è 1:1. Così, i composti con i cationi nei fori ottaedrici in una serie di anioni più vicini possono avere un rapporto massimo cationi:anioni di 1:1. In NiO, MnS, NaCl e KH, per esempio, tutti i fori ottaedrici sono riempiti. Rapporti inferiori a 1:1 si osservano quando alcuni dei fori ottaedrici rimangono vuoti.

In una semplice matrice cubica di anioni, c’è un foro cubico che può essere occupato da un catione per ogni anione della matrice. In CsCl, e in altri composti con la stessa struttura, tutti i fori cubici sono occupati. La metà dei fori cubici sono occupati in SrH2, UO2, SrCl2, e CaF2.

Diversi tipi di composti ionici spesso cristallizzano nella stessa struttura quando le dimensioni relative dei loro ioni e le loro stechiometrie (le due principali caratteristiche che determinano la struttura) sono simili.

Celle unitarie dei composti ionici

Molti composti ionici cristallizzano con celle unitarie cubiche, e useremo questi composti per descrivere le caratteristiche generali delle strutture ioniche.

Quando un composto ionico è composto da cationi e anioni di dimensioni simili in un rapporto 1:1, forma tipicamente una struttura cubica semplice. Il cloruro di cesio, CsCl, (illustrato nella figura 14) è un esempio di questo, con Cs+ e Cl- che hanno raggi di 174 pm e 181 pm, rispettivamente. Possiamo pensare a questo come ioni cloruro che formano una cella unitaria cubica semplice, con uno ione cesio al centro; o come ioni cesio che formano una cella unitaria con uno ione cloruro al centro; o come celle unitarie cubiche semplici formate da ioni Cs+ sovrapposte a celle unitarie formate da ioni Cl-. Gli ioni cesio e gli ioni cloruro si toccano lungo le diagonali del corpo delle celle unitarie. Uno ione cesio e uno ione cloruro sono presenti per cella unitaria, dando la stechiometria l:l richiesta dalla formula per il cloruro di cesio. Si noti che non c’è un punto di reticolo nel centro della cella, e CsCl non è una struttura BCC perché uno ione cesio non è identico a uno ione cloruro.

Figura 14. I composti ionici con cationi e anioni di dimensioni simili, come CsCl, di solito formano una struttura cubica semplice. Possono essere descritti da celle unitarie con cationi agli angoli o anioni agli angoli.

Abbiamo detto che la posizione dei punti del reticolo è arbitraria. Questo è illustrato da una descrizione alternativa della struttura CsCl in cui i punti di reticolo sono situati nei centri degli ioni di cesio. In questa descrizione, gli ioni di cesio si trovano sui punti di reticolo agli angoli della cella, e lo ione cloruro si trova al centro della cella. Le due celle unitarie sono diverse, ma descrivono strutture identiche.

Quando un composto ionico è composto da un rapporto 1:1 di cationi e anioni che differiscono significativamente in dimensioni, tipicamente cristallizza con una cella unitaria FCC, come quella mostrata in figura 15. Il cloruro di sodio, NaCl, è un esempio di questo, con Na+ e Cl- che hanno raggi di 102 pm e 181 pm, rispettivamente. Possiamo pensare a questo come a ioni cloruro che formano una cella FCC, con ioni di sodio situati nei fori ottaedrici al centro dei bordi della cella e al centro della cella. Gli ioni di sodio e di cloruro si toccano lungo i bordi della cella. La cella unitaria contiene quattro ioni sodio e quattro ioni cloruro, dando la stechiometria 1:1 richiesta dalla formula, NaCl.

Figura 15. I composti ionici con anioni che sono molto più grandi dei cationi, come NaCl, di solito formano una struttura FCC. Possono essere descritti da celle unitarie FCC con i cationi nei fori ottaedrici.

La forma cubica del solfuro di zinco, la blenda di zinco, cristallizza anche in una cella unitaria FCC, come illustrato nella figura 16. Questa struttura contiene ioni di solfuro sui punti di un reticolo FCC. (La disposizione degli ioni di solfuro è identica alla disposizione degli ioni di cloruro nel cloruro di sodio). Il raggio di uno ione di zinco è solo circa il 40% del raggio di uno ione solfuro, quindi questi piccoli ioni Zn2+ si trovano in fori tetraedrici alternati, cioè in una metà dei fori tetraedrici. Ci sono quattro ioni di zinco e quattro ioni di solfuro nella cella unitaria, dando la formula empirica ZnS.

Figura 16. ZnS, solfuro di zinco (o zinco blenda) forma una cella unitaria FCC con ioni di solfuro nei punti del reticolo e ioni di zinco molto più piccoli che occupano metà dei fori tetraedrici della struttura.

Una cella unitaria di fluoruro di calcio, come quella mostrata nella figura 17, è anch’essa una cella unitaria FCC, ma in questo caso, i cationi si trovano sui punti del reticolo; ioni di calcio equivalenti si trovano sui punti di un reticolo FCC. Tutti i siti tetraedrici nella matrice FCC degli ioni calcio sono occupati da ioni fluoruro. Ci sono quattro ioni calcio e otto ioni fluoruro in una cella unitaria, dando un rapporto calcio:fluoro di l:2, come richiesto dalla formula chimica, CaF2. Un attento esame della figura 17 rivelerà una semplice matrice cubica di ioni di fluoruro con ioni di calcio in una metà dei fori cubici. La struttura non può essere descritta in termini di un reticolo spaziale di punti sugli ioni fluoruro perché gli ioni fluoruro non hanno tutti ambienti identici. L’orientamento dei quattro ioni di calcio sugli ioni di fluoruro è diverso.

Figura 17. Il fluoruro di calcio, CaF2, forma una cella unitaria FCC con ioni calcio (verde) nei punti del reticolo e ioni fluoruro (rosso) che occupano tutti i siti tetraedrici tra loro.

Calcolo dei raggi ionici

Se conosciamo la lunghezza del bordo di una cella unitaria di un composto ionico e la posizione degli ioni nella cella, possiamo calcolare i raggi ionici per gli ioni nel composto se facciamo ipotesi sulle forme ioniche individuali e sui contatti.

Esempio 5: Calcolo dei raggi ionici

La lunghezza del bordo della cella unitaria di LiCl (struttura simile al NaCl, FCC) è 0.514 nm o 5,14 Å. Supponendo che lo ione litio sia abbastanza piccolo in modo che gli ioni cloruro siano in contatto, come nella figura 15, calcola il raggio ionico per lo ione cloruro.

Nota: L’unità di lunghezza angstrom, Å, è spesso usata per rappresentare dimensioni su scala atomica ed è equivalente a 10-10 m.

Mostra la soluzione

Sulla faccia di una cella unitaria LiCl, gli ioni cloruro si contattano a vicenda attraverso la diagonale della faccia:

Disegnando un triangolo rettangolo sulla faccia della cella unitaria, vediamo che la lunghezza della diagonale è uguale a quattro raggi di cloruro (un raggio da ogni angolo di cloruro e un diametro – che equivale a due raggi – dallo ione cloruro nel centro della faccia), quindi d = 4r. Dal teorema di Pitagora, abbiamo:

{{testo{a}}^{2}+{testo{a}}^{2}={{testo{d}}^{2}

che produce:

{sinistra(0.514{ nm}{ destra)^{2}+sinistra(0.514\text{ nm}\right)^{2}={\left(4r\right)}^{2}=16{r}^{2}

Solving this gives:

r=\sqrt{\dfrac{{(0.514\text{nm})}^{2}+{(0.514\text{nm})}^{2}}{16}}=\text{0.182 nm} (1,82 Å) per un raggio di Cl-

Check Your Learning

La lunghezza del bordo della cella unitaria di KCl (struttura NaCl-like, FCC) è 6,28 Å. Assumendo un contatto anione-catione lungo il bordo della cella, calcola il raggio dello ione potassio. Il raggio dello ione cloruro è 1,82 Å.

Mostra la soluzione

Il raggio dello ione potassio è 1,33 Å.

È importante rendersi conto che i valori dei raggi ionici calcolati dalle lunghezze dei bordi delle celle unitarie dipendono da numerosi presupposti, come una forma sferica perfetta per gli ioni, che sono al massimo delle approssimazioni. Quindi, tali valori calcolati sono essi stessi approssimativi e i confronti non possono essere spinti troppo in là. Tuttavia, questo metodo si è dimostrato utile per calcolare i raggi ionici da misure sperimentali come le determinazioni cristallografiche a raggi X.

Cristallografia a raggi X

La dimensione della cella unitaria e la disposizione degli atomi in un cristallo può essere determinata dalle misure della diffrazione dei raggi X da parte del cristallo, chiamata cristallografia a raggi X. La diffrazione è il cambiamento nella direzione di viaggio sperimentato da un’onda elettromagnetica quando incontra una barriera fisica le cui dimensioni sono paragonabili a quelle della lunghezza d’onda della luce. I raggi X sono radiazioni elettromagnetiche con lunghezze d’onda lunghe circa quanto la distanza tra gli atomi vicini nei cristalli (dell’ordine di qualche Å).

Quando un fascio di raggi X monocromatici colpisce un cristallo, i suoi raggi vengono dispersi in tutte le direzioni dagli atomi all’interno del cristallo. Quando le onde disperse che viaggiano nella stessa direzione si incontrano l’una con l’altra, subiscono un’interferenza, un processo attraverso il quale le onde si combinano per produrre un aumento o una diminuzione dell’ampiezza (intensità) a seconda della misura in cui i massimi delle onde combinate sono separati (vedi Figura 18).

Figura 18. Le onde luminose che occupano lo stesso spazio subiscono interferenza, combinandosi per produrre onde di maggiore (a) o minore (b) intensità, a seconda della separazione dei loro massimi e minimi.

Quando i raggi X di una certa lunghezza d’onda, λ, sono diffusi da atomi in piani di cristallo adiacenti separati da una distanza, d, possono subire interferenza costruttiva quando la differenza tra le distanze percorse dalle due onde prima della loro combinazione è un fattore intero, n, della lunghezza d’onda. Questa condizione è soddisfatta quando l’angolo del fascio diffratto, θ, è legato alla lunghezza d’onda e alla distanza interatomica dall’equazione:

n{lambda }=2d{sin}{theta

Questa relazione è nota come equazione di Bragg in onore di W. H. Bragg, il fisico inglese che per primo spiegò questo fenomeno. La figura 19 illustra due esempi di onde diffratte dagli stessi due piani di cristallo. La figura a sinistra mostra le onde diffratte all’angolo di Bragg, con conseguente interferenza costruttiva, mentre quella a destra mostra la diffrazione e un angolo diverso che non soddisfa la condizione di Bragg, con conseguente interferenza distruttiva.

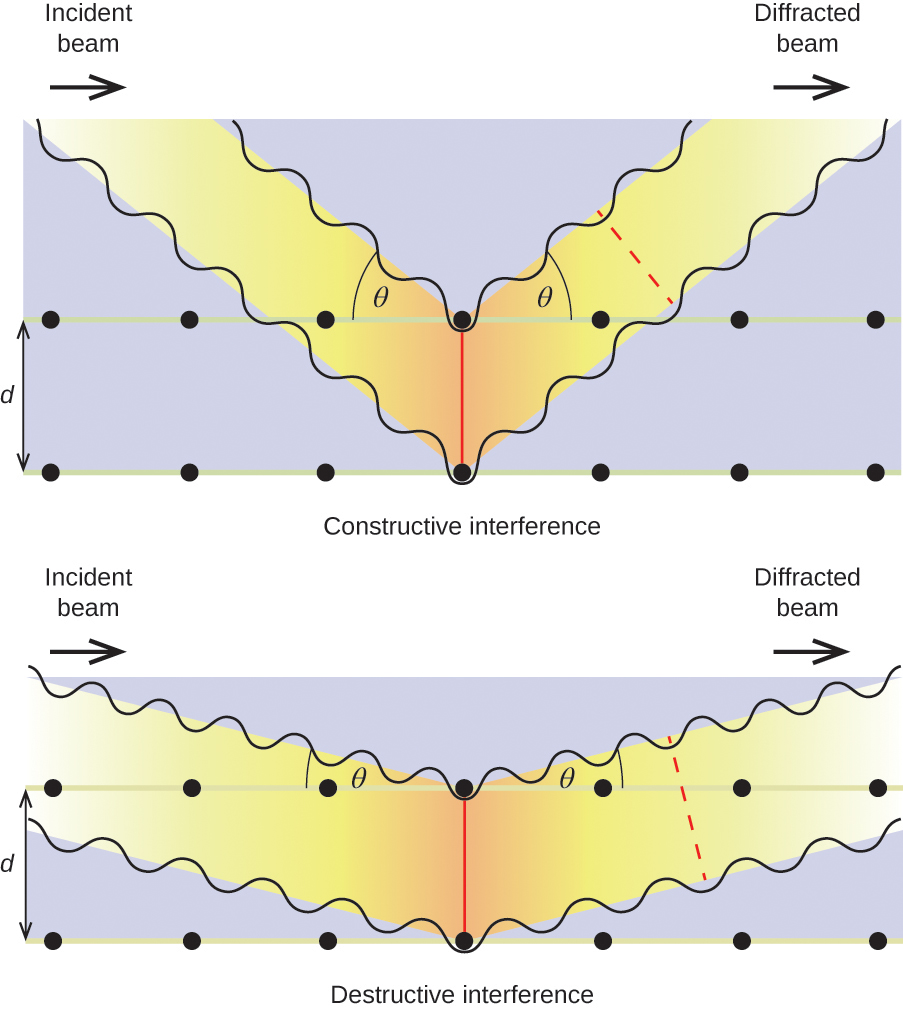
Figura 19. La diffrazione dei raggi X sparsi dagli atomi all’interno di un cristallo permette la determinazione della distanza tra gli atomi. L’immagine in alto mostra l’interferenza costruttiva tra due onde diffuse e un’onda diffratta risultante di alta intensità. L’immagine in basso mostra un’interferenza distruttiva e un’onda diffratta di bassa intensità.

Un diffrattometro a raggi X, come quello illustrato nella Figura 20, può essere usato per misurare gli angoli con cui i raggi X vengono diffratti quando interagiscono con un cristallo come descritto sopra. Da tali misurazioni, l’equazione di Bragg può essere usata per calcolare le distanze tra gli atomi, come dimostrato nel seguente esempio di esercizio.

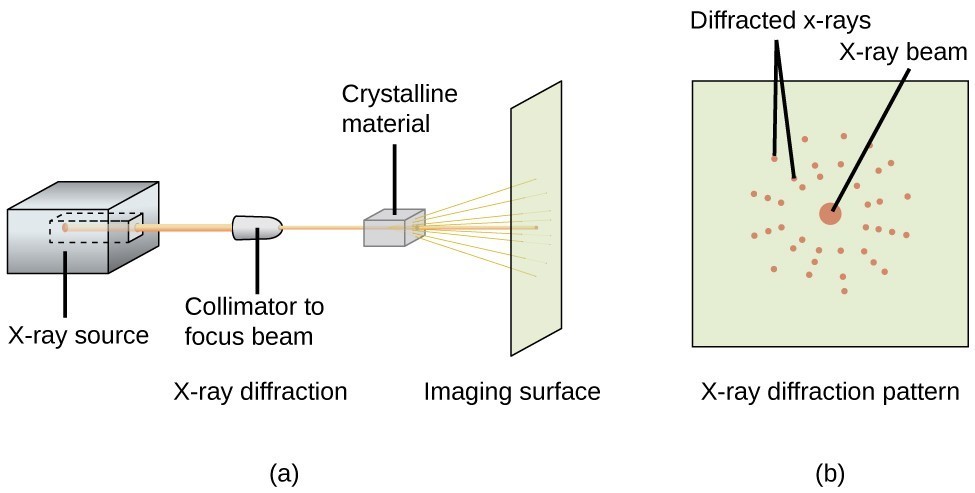
Figura 20. In un diffrattometro (a), un fascio di raggi X colpisce un materiale cristallino, producendo un modello di diffrazione dei raggi X (b) che può essere analizzato per determinare la struttura cristallina.

Puoi vedere la trascrizione di “Celebrating Crystallography – An animated adventure” qui (apre in una nuova finestra).

Ritratto di un chimico: Cristallografa a raggi X Rosalind Franklin

Figura 21. Questa illustrazione mostra un’immagine di diffrazione dei raggi X simile a quella trovata da Franklin nella sua ricerca. (credit: National Institutes of Health)

La scoperta della struttura del DNA nel 1953 da parte di Francis Crick e James Watson è uno dei grandi risultati nella storia della scienza. Hanno ricevuto il premio Nobel per la fisiologia o la medicina nel 1962, insieme a Maurice Wilkins, che ha fornito la prova sperimentale della struttura del DNA. La chimica britannica Rosalind Franklin ha dato un contributo inestimabile a questo monumentale risultato attraverso il suo lavoro di misurazione delle immagini di diffrazione dei raggi X del DNA. All’inizio della sua carriera, la ricerca della Franklin sulla struttura del carbone si rivelò utile allo sforzo bellico britannico. Dopo aver spostato la sua attenzione sui sistemi biologici all’inizio degli anni ’50, Franklin e lo studente di dottorato Raymond Gosling scoprirono che il DNA consiste di due forme: una fibra lunga e sottile che si forma quando è bagnata (tipo “B”) e una fibra corta e larga che si forma quando è essiccata (tipo “A”). Le sue immagini di diffrazione a raggi X del DNA (Figura 21) hanno fornito le informazioni cruciali che hanno permesso a Watson e Crick di confermare che il DNA forma una doppia elica, e di determinare i dettagli della sua dimensione e struttura.

Franklin ha anche condotto ricerche pionieristiche sui virus e sull’RNA che contiene le loro informazioni genetiche, scoprendo nuove informazioni che hanno cambiato radicalmente il corpo delle conoscenze nel campo. Dopo aver sviluppato un cancro alle ovaie, Franklin continuò a lavorare fino alla sua morte nel 1958 all’età di 37 anni. Tra i molti riconoscimenti postumi del suo lavoro, la Chicago Medical School della Finch University of Health Sciences ha cambiato il suo nome in Rosalind Franklin University of Medicine and Science nel 2004 e ha adottato un’immagine della sua famosa immagine della diffrazione a raggi X del DNA come logo ufficiale dell’università.

Glossario

cubo centrato (BCC) solido: struttura cristallina che ha una cella cubica con punti di reticolo agli angoli e al centro della cella

cella cubica centrata sul corpo: unità ripetitiva più semplice di un cristallo cubico a corpo centrato; è un cubo contenente punti di reticolo ad ogni angolo e al centro del cubo

equazione di Bragg: equazione che mette in relazione gli angoli con cui i raggi X vengono diffratti dagli atomi all’interno di un cristallo

numero di coordinazione: numero di atomi più vicini ad un dato atomo in un cristallo o all’atomo centrale del metallo in un complesso

cubic closest packing (CCP): struttura cristallina in cui piani di atomi o ioni strettamente impacchettati sono impilati come una serie di tre strati alternati di diversi orientamenti relativi (ABC)

diffrazione: reindirizzamento della radiazione elettromagnetica che avviene quando incontra una barriera fisica di dimensioni appropriate

solido cubico a facce centrate (FCC): struttura cristallina costituita da una cella cubica con punti di reticolo agli angoli e al centro di ogni faccia

cella cubica a facce centrate: unità ripetitiva più semplice di un cristallo cubico a facce centrate; è un cubo contenente punti di reticolo ad ogni angolo e al centro di ogni faccia

hexagonal closest packing (HCP): struttura cristallina in cui strati ravvicinati di atomi o ioni sono impilati come una serie di due strati alternati di differenti orientamenti relativi (AB)

hole: (anche, interstizio) spazio tra gli atomi all’interno di un cristallo

isomorfo: che possiede la stessa struttura cristallina

foro ottaedrico: spazio aperto in un cristallo al centro di sei particelle situate agli angoli di un ottaedro

cella cubica semplice: (anche, cella unitaria cubica primitiva) cella unitaria nella struttura cubica semplice

struttura cubica semplice: struttura cristallina con una cella unitaria cubica con punti di reticolo solo agli angoli

reticolo spaziale: tutti i punti in un cristallo che hanno ambienti identici

foro tetraedrico: spazio tetraedrico formato da quattro atomi o ioni in un cristallo

cella unitaria: la più piccola porzione di un reticolo spaziale che si ripete in tre dimensioni per formare l’intero reticolo

cristallografia a raggi X: tecnica sperimentale per determinare le distanze tra gli atomi in un cristallo misurando gli angoli di diffrazione dei raggi X quando attraversano il cristallo

.