Durante il XVII e soprattutto il XVIII secolo, spinti sia dal desiderio di capire la natura che dalla ricerca di costruire palloni in cui poter volare (Figura 1), alcuni scienziati stabilirono le relazioni tra le proprietà fisiche macroscopiche dei gas, cioè pressione, volume, temperatura e quantità di gas. Anche se le loro misurazioni non erano precise per gli standard odierni, furono in grado di determinare le relazioni matematiche tra le coppie di queste variabili (ad esempio, pressione e temperatura, pressione e volume) che valgono per un gas ideale, un costrutto ipotetico che i gas reali approssimano in certe condizioni. Alla fine, queste leggi individuali sono state combinate in un’unica equazione – la legge dei gas ideali – che mette in relazione le quantità di gas per i gas ed è abbastanza accurata per basse pressioni e temperature moderate. Considereremo gli sviluppi chiave nelle relazioni individuali (per ragioni pedagogiche non proprio in ordine storico), poi li metteremo insieme nella legge dei gas ideali.

Figura 1. Nel 1783, si sono verificati il primo (a) volo in pallone aerostatico pieno di idrogeno, (b) volo in mongolfiera con equipaggio, e (c) volo in pallone aerostatico pieno di idrogeno con equipaggio. Quando il pallone ad idrogeno raffigurato in (a) atterrò, gli abitanti spaventati di Gonesse lo distrussero con forconi e coltelli. Il lancio di quest’ultimo fu visto da 400.000 persone a Parigi.

Pressione e temperatura: Legge di Gay-Lussac

Immaginate di riempire di gas un contenitore rigido collegato a un manometro e poi di sigillare il contenitore in modo che il gas non possa uscire. Se il contenitore viene raffreddato, il gas all’interno diventa più freddo e si osserva che la sua pressione diminuisce. Poiché il contenitore è rigido e ben sigillato, sia il volume che il numero di moli di gas rimangono costanti. Se riscaldiamo la sfera, il gas all’interno diventa più caldo (figura 2) e la pressione aumenta.

Figura 2. L’effetto della temperatura sulla pressione del gas: Quando la piastra è spenta, la pressione del gas nella sfera è relativamente bassa. Man mano che il gas viene riscaldato, la pressione del gas nella sfera aumenta.

Questa relazione tra temperatura e pressione si osserva per qualsiasi campione di gas confinato in un volume costante. Un esempio di dati sperimentali pressione-temperatura è mostrato per un campione di aria in queste condizioni nella figura 3. Troviamo che la temperatura e la pressione sono linearmente correlate, e se la temperatura è sulla scala kelvin, allora P e T sono direttamente proporzionali (di nuovo, quando volume e moli di gas sono tenuti costanti); se la temperatura sulla scala kelvin aumenta di un certo fattore, la pressione del gas aumenta dello stesso fattore.

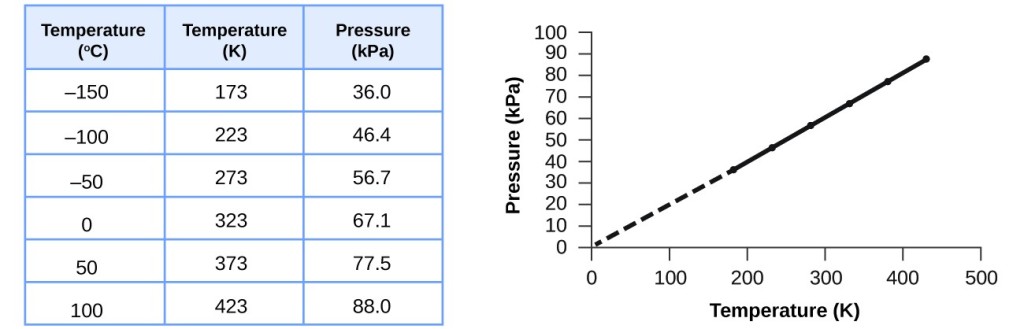
Figura 3. Per un volume e una quantità d’aria costanti, la pressione e la temperatura sono direttamente proporzionali, purché la temperatura sia in kelvin. (Le misure non possono essere fatte a temperature inferiori a causa della condensazione del gas). Quando questa linea viene estrapolata a pressioni più basse, raggiunge una pressione di 0 a -273 °C, che è 0 sulla scala kelvin e la più bassa temperatura possibile, chiamata zero assoluto.

Guillaume Amontons fu il primo a stabilire empiricamente la relazione tra la pressione e la temperatura di un gas (~1700), e Joseph Louis Gay-Lussac determinò la relazione più precisamente (~1800). Per questo motivo, la relazione P-T per i gas è conosciuta come legge di Gay-Lussac o legge di Amontons. Sotto entrambi i nomi, afferma che la pressione di una data quantità di gas è direttamente proporzionale alla sua temperatura sulla scala kelvin quando il volume è tenuto costante. Matematicamente, questo può essere scritto:

grande P=proto T

grande P=costante di testo

grande P=k=tempi T

dove ∝ significa “è proporzionale a”, e k è una costante di proporzionalità che dipende dall’identità, quantità e volume del gas.

grandiosofrac{P}_{1}}{T}_{1}}=frac{P}_{2}{T}_{2}

Questa equazione è utile per calcoli di pressione-temperatura per un gas confinato a volume costante. Si noti che le temperature devono essere sulla scala kelvin per qualsiasi calcolo della legge dei gas (0 sulla scala kelvin e la più bassa temperatura possibile è chiamata zero assoluto). (Notate anche che ci sono almeno tre modi per descrivere come la pressione di un gas cambia al variare della sua temperatura: Possiamo usare una tabella di valori, un grafico o un’equazione matematica.)

Volume e temperatura: Legge di Charles

Se riempiamo un palloncino con aria e lo sigilliamo, il palloncino contiene una quantità specifica di aria alla pressione atmosferica, diciamo 1 atm. Se mettiamo il palloncino in un frigorifero, il gas all’interno si raffredda e il palloncino si restringe (anche se sia la quantità di gas che la pressione rimangono costanti). Se rendiamo il palloncino molto freddo, si restringe molto, e si espande di nuovo quando si riscalda.

Questi esempi dell’effetto della temperatura sul volume di una data quantità di un gas confinato a pressione costante sono veri in generale: Il volume aumenta all’aumentare della temperatura e diminuisce al diminuire della temperatura. I dati di volume-temperatura per un campione di 1 mole di gas metano a 1 atm sono elencati e rappresentati graficamente nella figura 4.

Figura 4. Il volume e la temperatura sono linearmente correlati per 1 mole di gas metano ad una pressione costante di 1 atm. Se la temperatura è in kelvin, volume e temperatura sono direttamente proporzionali. La linea si ferma a 111 K perché il metano si liquefa a questa temperatura; se estrapolata, interseca l’origine del grafico, che rappresenta una temperatura di zero assoluto.

La relazione tra il volume e la temperatura di una data quantità di gas a pressione costante è nota come legge di Charles in riconoscimento dello scienziato francese e pioniere del volo in mongolfiera Jacques Alexandre César Charles. La legge di Charles afferma che il volume di una data quantità di gas è direttamente proporzionale alla sua temperatura sulla scala kelvin quando la pressione è tenuta costante.

Matematicamente, questo può essere scritto come:

grande V\proto T

grande V=costante V=k\cdot T

grande V=k\cdot T

con k una costante di proporzionalità che dipende dalla quantità e dalla pressione del gas.

grandioso=frac{V}_{1}}{T}_{1}}=frac{V}_{2}{T}_{2}}

Volume e pressione: legge di Boyle

Se riempiamo parzialmente una siringa ermetica con aria, la siringa contiene una quantità specifica di aria a temperatura costante, diciamo 25 °C. Se spingiamo lentamente lo stantuffo mantenendo la temperatura costante, il gas nella siringa viene compresso in un volume minore e la sua pressione aumenta; se tiriamo fuori lo stantuffo, il volume aumenta e la pressione diminuisce. Questo esempio dell’effetto del volume sulla pressione di una data quantità di un gas confinato è vero in generale. Diminuendo il volume di un gas contenuto aumenterà la sua pressione, e aumentando il suo volume diminuirà la sua pressione. Infatti, se il volume aumenta di un certo fattore, la pressione diminuisce dello stesso fattore, e viceversa. I dati di volume-pressione per un campione di aria a temperatura ambiente sono rappresentati graficamente nella figura 5.

Figura 5. Quando un gas occupa un volume minore, esercita una pressione maggiore; quando occupa un volume maggiore, esercita una pressione minore (assumendo che la quantità di gas e la temperatura non cambino). Poiché P e V sono inversamente proporzionali, un grafico di 1/P contro V è lineare.

A differenza delle relazioni P-T e V-T, pressione e volume non sono direttamente proporzionali tra loro. Invece, P e V mostrano una proporzionalità inversa: Aumentando la pressione si ha una diminuzione del volume del gas. Matematicamente questo può essere scritto:

grande P\proto 1\testo{/}V\testo{ o }P=k\cdot 1\testo{/}V\testo{ o }P\cdot V=k\testo{ o {P}_{1}{V}_{1}={P}_{2}{V}_{2}

con k come costante. Graficamente, questa relazione è mostrata dalla linea retta che risulta quando si traccia l’inverso della pressione \large\left(\frac{1}{P}destra) contro il volume (V), o l’inverso del volume \large\left(\frac{1}{V}destra) contro la pressione (V). I grafici con linee curve sono difficili da leggere accuratamente a valori bassi o alti delle variabili, e sono più difficili da usare per adattare equazioni teoriche e parametri ai dati sperimentali. Per queste ragioni, gli scienziati spesso cercano di trovare un modo per “linearizzare” i loro dati. Se tracciamo P contro V, otteniamo un’iperbole (vedi figura 6).

La relazione tra il volume e la pressione di una data quantità di gas a temperatura costante fu pubblicata per la prima volta dal filosofo naturale inglese Robert Boyle oltre 300 anni fa. È riassunta nell’affermazione ora nota come legge di Boyle: Il volume di una data quantità di gas a temperatura costante è inversamente proporzionale alla pressione sotto la quale è misurato.

La chimica in azione: La respirazione e la legge di Boyle

Cosa fai circa 20 volte al minuto per tutta la vita, senza pausa, e spesso senza nemmeno esserne consapevole? La risposta, naturalmente, è la respirazione. Come funziona? Si scopre che qui si applicano le leggi dei gas. I tuoi polmoni assorbono il gas di cui il tuo corpo ha bisogno (ossigeno) e si liberano del gas di scarto (anidride carbonica). I polmoni sono fatti di tessuto spugnoso ed elastico che si espande e si contrae mentre respiri. Quando inspiri, il diaframma e i muscoli intercostali (i muscoli tra le costole) si contraggono, espandendo la cavità toracica e aumentando il volume dei polmoni. L’aumento di volume porta ad una diminuzione della pressione (legge di Boyle). Questo fa sì che l’aria fluisca nei polmoni (da alta pressione a bassa pressione). Quando espiri, il processo si inverte: Il diaframma e i muscoli delle costole si rilassano, la cavità toracica si contrae e il volume dei polmoni diminuisce, causando un aumento della pressione (di nuovo la legge di Boyle), e l’aria esce dai polmoni (da alta pressione a bassa pressione). Poi inspiri ed espiri ancora, e ancora, ripetendo questo ciclo della legge di Boyle per il resto della tua vita (Figura 7).

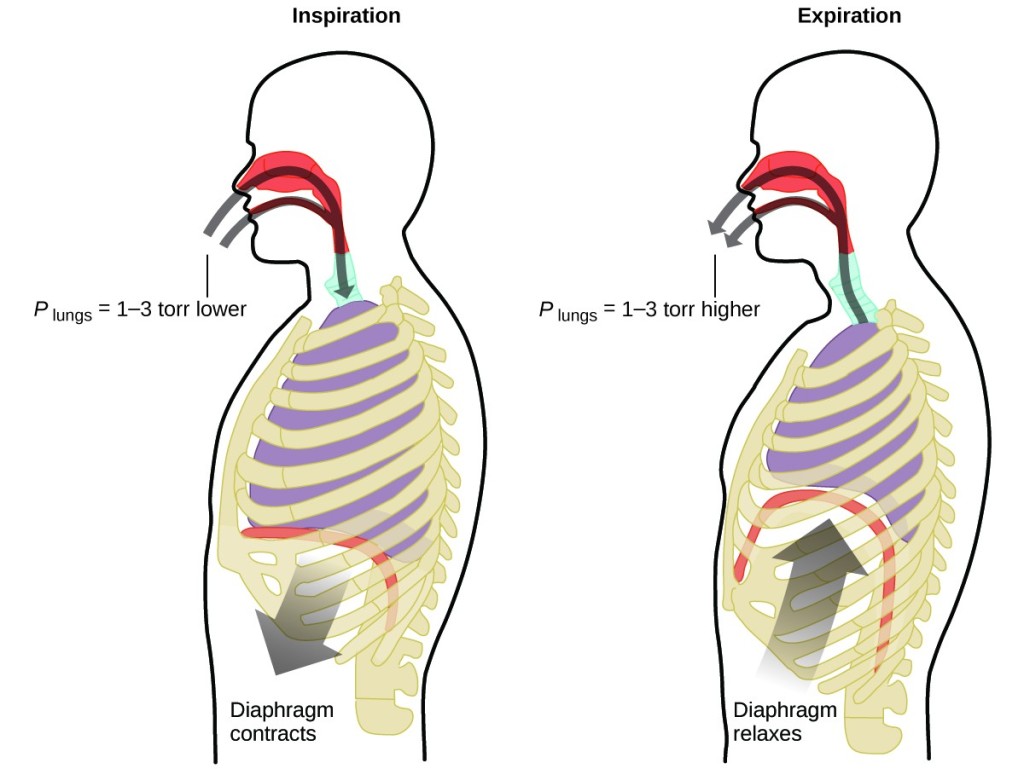
Figura 7. La respirazione avviene perché l’espansione e la contrazione del volume dei polmoni crea piccole differenze di pressione tra i polmoni e l’ambiente circostante, facendo sì che l’aria venga aspirata e spinta fuori dai polmoni.

Moli di gas e volume: Legge di Avogadro

Lo scienziato italiano Amedeo Avogadro avanzò un’ipotesi nel 1811 per spiegare il comportamento dei gas, affermando che volumi uguali di tutti i gas, misurati nelle stesse condizioni di temperatura e pressione, contengono lo stesso numero di molecole. Nel corso del tempo, questa relazione è stata supportata da molte osservazioni sperimentali come espresso dalla legge di Avogadro: Per un gas confinato, il volume (V) e il numero di moli (n) sono direttamente proporzionali se la pressione e la temperatura rimangono entrambe costanti.

In forma di equazione, questo è scritto come:

grandioso{begin{array}{ccccc}V\proto n& \testo{o}& V=k\times n& \testo{o}& \frac{V}{V}{1}}{n}_{1}}=\frac{V}_{2}}{n}_{2}}end{array}

Rapporti matematici possono essere determinati anche per le altre coppie di variabili, come P contro n, e n contro T.

Glossario

Zero assoluto: temperatura alla quale il volume di un gas sarebbe zero secondo la legge di Charles.

Legge di Avogadro: il volume di un gas a temperatura e pressione costante è proporzionale al numero di molecole di gas

Legge di Boyle: il volume di un dato numero di moli di gas a temperatura costante è inversamente proporzionale alla pressione sotto la quale è misurato

Legge di Charles: il volume di un dato numero di moli di gas è direttamente proporzionale alla sua temperatura kelvin quando la pressione è tenuta costante

legge di Gay-Lussac: (anche, legge di Amontons) la pressione di un dato numero di moli di gas è direttamente proporzionale alla sua temperatura kelvin quando il volume è tenuto costante

.