A che cosa servono le tabelle dei caratteri?

A questo punto una buona domanda è: a che serve imparare le tabelle dei caratteri? La risposta semplice è che la simmetria e la tabella dei caratteri associata di una molecola possono essere usate per interpretare e prevedere molti aspetti delle spettroscopie chimicamente significative, così come il legame. Lo illustreremo ora concentrandoci sui modi vibrazionali di una molecola.

In laboratorio possiamo raccogliere dati sperimentali utili usando la spettroscopia infrarossa (IR) e Raman. Questi dati possono essere confrontati con il numero di bande attive IR e/o Raman previste dall’applicazione della teoria dei gruppi e della tabella dei caratteri corretta. La matematica (teoria dei gruppi e algebra delle matrici) dietro questo trattamento serve come solida base teorica. Le manipolazioni descritte di seguito funzionano perché tutte le operazioni di simmetria di una molecola comprendono un gruppo matematico e obbediscono alle regole del gruppo. Come notato in precedenza, non dobbiamo padroneggiare quest’area della matematica per fare buon uso delle tabelle dei caratteri.

Gradi di libertà e vibrazioni nelle molecole

Qui discuteremo inizialmente i gradi di libertà per una molecola semplice (l’acqua). Vedremo molto rapidamente perché è molto utile impiegare la simmetria quando si studiano molecole più grandi.

Per una molecola con “N” atomi ci sono 3N gradi di libertà (ricordate che viviamo in un mondo tridimensionale di coordinate x, y, z). Per una molecola non lineare, 3 gradi di libertà possono essere firmati alle traslazioni – movimento di un corpo nel suo insieme (Tx, Ty, Tz) e 3 alle rotazioni (Rx, Ry, Rz). I restanti movimenti degli atomi sono spostamenti degli atomi dalle loro posizioni medie – il centro di gravità non cambia. Queste vibrazioni fondamentali sono chiamate “modi normali”. Così, una molecola non lineare ha 3N-6 modi normali. Per l’acqua il numero di modi normali è 3 (3 x 3 – 6 = 3). Per le molecole lineari ci sono 3N-5 modi normali.

Per l’acqua, che naturalmente è stata studiata intensamente, sappiamo che le 3 vibrazioni sono le seguenti.

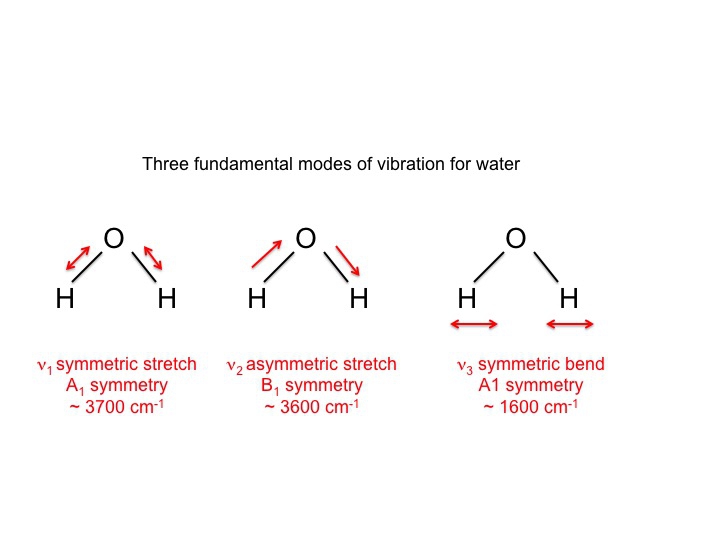
I simboli usati per descrivere questi modi (A1, B1) sono gli stessi simboli Mulliken che abbiamo incontrato nella nostra discussione sulle tabelle dei caratteri. In altre parole, le vibrazioni, che sono proprietà molecolari, possono essere descritte da specie di simmetria o rappresentazioni irriducibili. Infatti gran parte della letteratura che riguarda la spettroscopia vibrazionale usa questi simboli come un modo sintetico di comunicare le informazioni.

Dovrebbe essere abbastanza ovvio che il numero di vibrazioni aumenta rapidamente con aumenti anche modesti del numero di atomi nella molecola. Determinare i tipi di vibrazioni per ispezione (come abbiamo fatto per l’acqua) diventa ora molto più difficile. Per esempio, consideriamo i seguenti composti:

H2O 3 atomi 3 vibrazioni

PH3 4 atomi 6 vibrazioni

CO22- 4 atomi 6 vibrazioni

XeF4 5 atomi 9 vibrazioni

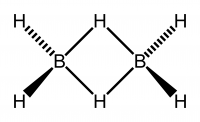
B2H6 8 atomi 18 vibrazioni

Per il diborano (B2H6) che ha simmetria D2h capire la natura e le specie di simmetria di tutte le 18 vibrazioni tramite ispezione sarebbe un compito arduo. Tuttavia, armati della tabella dei caratteri per D2h e della conoscenza delle proprietà di simmetria, il compito di determinare la specie di simmetria di tutte le vibrazioni è immediato.

Per il caso dell’acqua potremmo presentare la tabella dei caratteri (C2v) con le 3 vibrazioni (ν1, v2, v3) elencate nella colonna delle proprietà molecolari come mostrato sotto. (ν = simbolo greco “nu”)

Tuttavia, in generale questo approccio è poco pratico. Prendiamo ad esempio la piridina (C5H5N). Il gruppo fondamentale è anche C2v ma la molecola ha 11 atomi. Il numero di modi fondamentali di vibrazione è 27 ( 3 x 11 – 6 = 27).

In questo caso dovremmo redigere una tabella dei caratteri C2v che mostra le simmetrie di tutte le 27 vibrazioni. Per questo motivo le vibrazioni non sono normalmente incluse nelle tabelle dei caratteri. Spetta invece all’utente (voi) determinare il numero e il tipo di vibrazioni (come definito dalle loro specie di simmetria) per ogni molecola che si incontra. Il modo in cui lo facciamo è descritto di seguito.

Rappresentazioni riducibili

Come notato in precedenza, una delle importanti proprietà delle tabelle di caratteri è che le operazioni di simmetria sono membri di un gruppo matematico ed esistono importanti relazioni tra loro. In generale, lo stesso si può dire delle specie di simmetria o rappresentazioni irriducibili delle proprietà molecolari. I prodotti della combinazione dei caratteri delle rappresentazioni irriducibili, sia per moltiplicazione che per addizione/sottrazione, obbediscono anch’essi alle regole del gruppo. Le nuove rappresentazioni non sono più le più semplici possibili e sono chiamate “rappresentazioni riducibili” perché possono essere “ridotte” alle loro parti componenti.

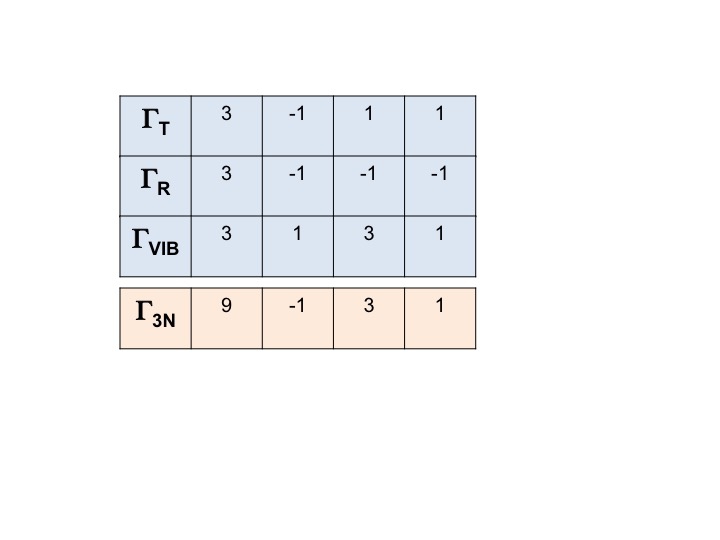
Ad esempio, per l’acqua le simmetrie delle traslazioni (Tx, Ty, Tz) possono essere ricavate direttamente dalla tabella dei caratteri C2v. Sono A1, B1 e B2. Possiamo rappresentare tutti e tre questi gradi di libertà con una rappresentazione ΓT e possiamo scrivere l’espressione sottostante. (Γ = lettera greca maiuscola “gamma”).

ΓT = A1 + B1 + B2

Sappiamo che A1, B1 e B2 sono semplicemente le notazioni stenografiche per le specie di simmetria (rappresentazioni irriducibili). Possiamo quindi semplicemente scrivere i caratteri di ΓT aggiungendo i singoli caratteri per A1, B1 e B2 dalla tabella dei caratteri C2v.

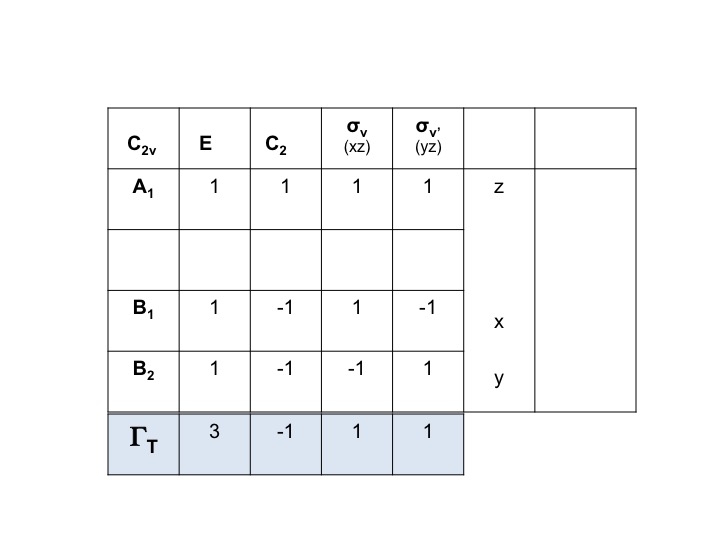
Quindi ΓT = 3 -1 1 1.

Questa è una rappresentazione riducibile valida e un membro del gruppo C2v.

In modo simile possiamo scrivere la rappresentazione riducibile per tutte e tre le rotazioni e tutte le vibrazioni.

La rappresentazione per TUTTI i gradi di libertà della molecola (3N) può essere scritta come

Γ3N = ΓT + ΓR + ΓVIB

e la rappresentazione riducibile per essa si ottiene semplicemente sommando i caratteri di ΓT, ΓR e ΓVIB.

Γ3N = 9 -1 3 1

Prendi nota di questo – verrà fuori più tardi!

Anche se l’insieme dei caratteri 9 -1 3 1 è un membro valido del gruppo C2v non è particolarmente utile quando si parla di proprietà molecolari. Ciò che è veramente necessario è il linguaggio delle specie di simmetria stenografiche (simboli di Mulliken, A1, B1 ecc.). In altre parole vogliamo esprimere Γ3N in termini di A1, B1 ecc. Dalle informazioni di cui sopra può essere facilmente dimostrato per ispezione che:

Γ3N = 3A1 +A2 + 3B1 +2B2

La buona notizia è che per altre molecole più complesse non dobbiamo eseguire questo compito per ispezione perché:

1. Possiamo facilmente generare Γ3N come rappresentazione riducibile per una molecola (se conosciamo il suo gruppo di simmetria puntiforme).

2. Possiamo facilmente convertire la rappresentazione riducibile Γ3N nella somma delle sue specie di simmetria (simboli Mulliken) usando una formula “semplice” conosciuta come formula di riduzione.

Metodo generale per ottenere Γ3N

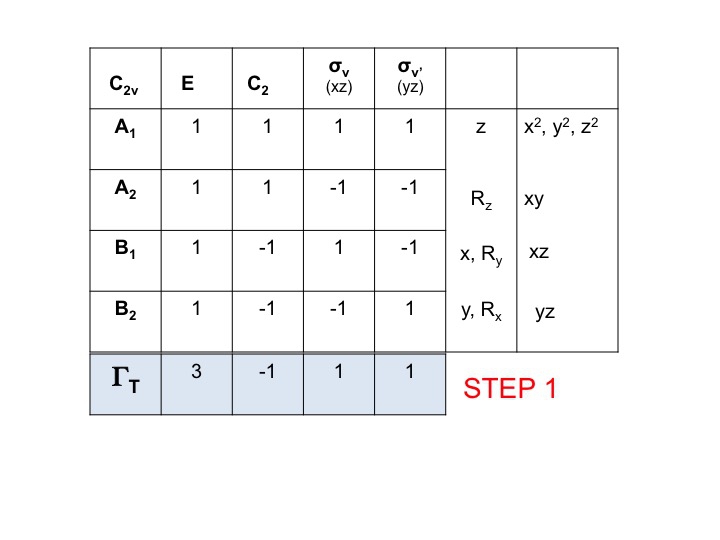
Passo 1

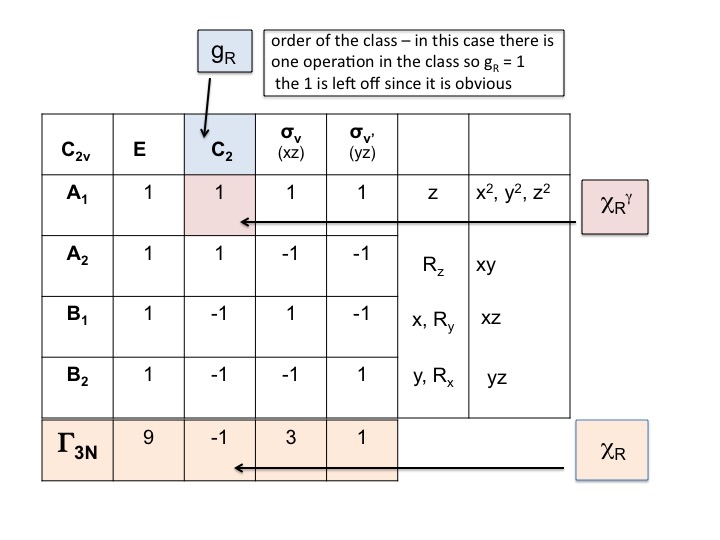
Prendere la tabella dei caratteri della molecola e aggiungere una riga in basso. In questa riga genera la rappresentazione riducibile per ΓT (o Γxyz) come abbiamo fatto sopra, semplicemente aggiungendo i caratteri per ogni operazione che corrispondono alle proprietà molecolari per x, y e z. Per C2v abbiamo già mostrato che questi sono i caratteri corrispondenti a A1, B1 e B2.

Passo 2

Aggiungi un’altra riga sotto ΓT e scrivi il numero di atomi che NON CAMBIANO la loro posizione durante ogni operazione di simmetria. Questo è il momento in cui ti rendi conto di quanto sia utile un set di modelli molecolari reali. Per fare questo avrete anche bisogno di sapere dove sono gli elementi di simmetria e come le operazioni di simmetria influenzano la molecola. Naturalmente, sapete già come fare questo perché avete studiato la notazione di Schönflies e sapete come assegnare il gruppo di punti di una molecola. La tabella dei caratteri ha anche tutte le operazioni di simmetria elencate per classe lungo la riga superiore.

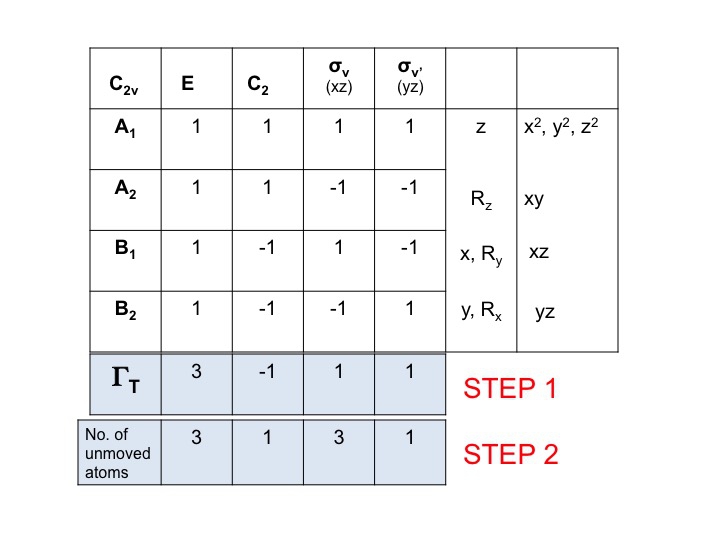
Così per l’acqua (3 atomi) sotto E ci sono 3 atomi non spostati, ma per C2 entrambe le H si muovono ma poiché l’atomo O si trova sull’asse C2 non cambia la sua posizione e quindi registriamo 1 sotto la colonna C2. Il nuovo insieme di numeri generato nel passo 2 (3 1 3 1) è anche una rappresentazione riducibile in C2v e obbedisce alle regole del gruppo.

Passo 3

In questo passo semplicemente moltiplichiamo insieme i caratteri che sono stati generati nei passi 1 e 2. Il risultato (terza riga) è la rappresentazione riducibile per Γ3N (o ΓTOT). È così semplice.

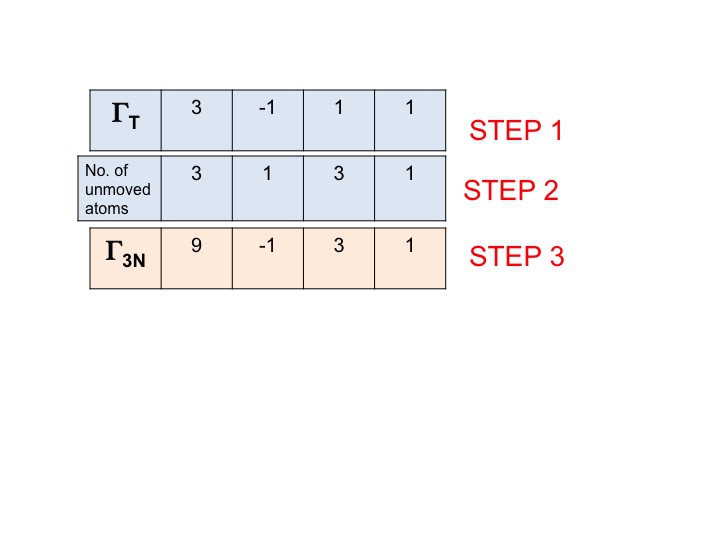
Si noterà che la nuova rappresentazione riducibile (9 -1 1 3) è identica alla rappresentazione per Γ3N che abbiamo ottenuto precedentemente per ispezione.

Riduzione della rappresentazione riducibile

Per convertire QUALSIASI rappresentazione riducibile nella somma delle sue rappresentazioni irriducibili (specie di simmetria o simboli di Mulliken) usiamo una formula di riduzione:

Puoi trovare facilmente questa informazione nella tabella dei caratteri:

Torna al nostro esempio dell’acqua: Gruppo puntiforme C2v, ordine (g) = 4

La rappresentazione riducibile per Γ3N = 9 -1 3 1

Il numero di volte che A1 appare in questa rappresentazione è quindi

aA1 = 1/4 { 1.1.9 + 1.1. (-1) + 1.1.3 +1.1.1} = 3

quindi Γ3N contiene 3 specie di simmetria A1. I numeri delle altre specie di simmetria sono calcolati come segue:

aA2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1).3 + 1.(-1).1 } = 1 una A2 presente

aB1 = 1/4 { 1.1.9 + 1.(-1).(-1) + 1.1.3 + 1.(-1).1} = 3 3 B1 presente

aB2 = 1/4 {1.1.9 + 1.(-1)(-1) + 1.(-1).3 + 1.1.1} = 2 2 B2 presente

Possiamo ora scrivere Γ3N = 3A1 + A2 + 3B1 + 2B2 (esattamente quello che abbiamo ottenuto per “ispezione” sopra. Possiamo ora sottrarre le specie di simmetria per le traslazioni e le rotazioni e questo ci darà il numero e le specie di simmetria dei modi fondamentali di vibrazione. ΓT e ΓR possono essere ottenuti direttamente dalla tabella dei caratteri.

Γ3N = 3A1 + A2 + 3B1 + 2B2

ΓT = A1 + B1 + B2

ΓR = A2 + B1 + B2

ΓVIB = Γ3N – ΓT – ΓR = 2A1 +B1

Quindi i tre modi normali di vibrazione dell’acqua hanno le simmetrie A1, A1 e B1.

Abbiamo ora un metodo generale per determinare tutti i modi di vibrazione fondamentali di una molecola ed esprimere questi modi nel linguaggio stenografico dei simboli di Mulliken. Questo è uno degli esercizi su cui sarete esaminati nell’esame 1. Il modo migliore per prendere confidenza con questo metodo è fare pratica con quanti più esempi possibili!

Prossimo: Regole di selezione

.