Less…
A Pitagorasz hármasa a 
, 
és 
pozitív egész számok olyan hármasa, hogy létezik egy derékszögű háromszög, amelynek lábai 
és hipotenúzája 
. A Pitagorasz-tétel alapján ez egyenértékű azzal, hogy olyan pozitív egész számokat 
, 
és 
találunk, amelyek kielégítik a
 |
(1)
|
A legkisebb és legismertebb Pitagorasz-hármas 
. Az ilyen oldalhosszúságú derékszögű háromszöget néha 3,4,5 háromszögnek nevezik.
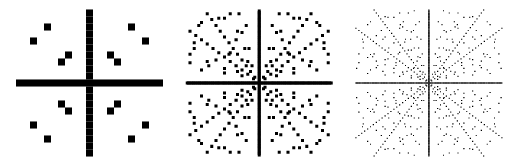
A 
-sík olyan pontjainak ábrázolása, hogy 
egy Pitagorasz-háromszög, a fentiekben egymás után következő nagyobb határok esetén látható. Ezek az ábrák tartalmazzák 
és 
negatív értékeit, és ezért mind az x-, mind az y-tengelyre szimmetrikusak.
Hasonlóképpen, a 
-síkon lévő olyan pontok ábrái, hogy 
egy Pitagorasz-hármas, egymás után nagyobb korlátok esetén láthatóak fent.
Szokás csak olyan primitív Pitagorasz-hármasokat (más néven “redukált “hármasokat) vizsgálni, amelyekben 
és 
viszonylag prímek, mivel a primitívekből triviálisan előállíthatók más megoldások. A primitív hármasokat fentebb ábrázoltuk, és azonnal látható, hogy az eredeti ábrán szereplő imprimitív hármasoknak megfelelő sugárirányú vonalak hiányoznak ezen az ábrán. A primitív megoldásoknál a 
vagy 
közül az egyiknek párosnak, a másiknak pedig páratlannak kell lennie (Shanks 1993, 141. o.), a 
mindig páratlan.
Ezeken kívül minden Pitagorasz-hármas egyik oldala osztható 3-mal, egy másik 4-gyel, egy harmadik pedig 5-tel. Az egyik oldalnak lehet két ilyen osztója, mint a (8, 15, 17), (7, 24, 25) és (20, 21, 29), vagy akár mindhárom, mint a (11, 60, 61).
Adva egy 
primitív hármasból
 |
 |
 |
(2)
|
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
hol
 |
 |
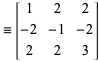(5)
|
 |
 |
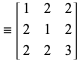(6)
|
 |
 |
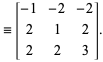(7)
|
Hall (1970) és Roberts (1977) bizonyítják, hogy 
egy primitív püthagoreus hármas, ha
 |
(8)
|
ahol 
a 
, 
, 
mátrixok véges szorzata. Ebből következik, hogy minden primitív Pitagorasz-hármasnak a végtelen tömb
 |
(9)
|
Pythagorasz és a babiloniak a következő képletet adták meg a (nem feltétlenül primitív) hármasok előállítására:
 |
(10)
|
for 
, amely olyan különböző hármasok halmazát generálja, amely nem tartalmaz sem minden primitív, sem minden imprimitív hármasokat (és ahol a speciális esetben 
, 
).
A korai görögök adták
 |
(11)
|
ahol 
és 
viszonylag prímek és ellentétes paritásúak (Shanks 1993, p. 141), ami olyan különböző hármasok halmazát generálja, amely pontosan a primitív hármasokat tartalmazza (a 
és 
megfelelő rendezése után).
Legyen 
egy Fibonacci-szám. Akkor
 |
(12)
|
különböző Pitagorasz-hármasokat generál (Dujella 1995), bár nem kimerítően sem primitív, sem imprimitív hármasokra. Általánosabban, a 
, 
pozitív egész számokból kiindulva és a 
Fibonacci-szerű sorozatot 
, 
, 
, 
, 
, … generál különböző Pitagorasz-hármasokat
 |
(13)
|
(Horadam 1961), ahol
 |
(24)
|
(Beiler 1966, p. 116). Megjegyezzük, hogy 
, ha 
prím vagy kétszer prím. Az első néhány szám 
, 2, … esetén 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 4, 1, …. (OEIS A046079).
Az 
azon módok számának megtalálásához, amelyekkel egy 
szám lehet egy primitív derékszögű háromszög hipotenuzája, írjuk fel a faktorizációját a következőképpen:
 |
(25)
|
ahol a 
s az 
, a 
s pedig az 
alakú. A lehetséges primitív derékszögű háromszögek száma tehát
 |
(26)
|
Például, 
hiszen
 |
 |
 |
(27)
|
 |
 |
 |
(28)
|
A 
értékei 
, 2, … esetén 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, …. (OEIS A024362). Az első néhány 
alakú prímszám az 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, … (OEIS A002144), tehát az 1, 2, 4, 8, 16, … primitív derékszögű háromszögek hipoténuszaihoz tartozó legkisebb oldalhosszúságok: 5, 65, 1105, 32045, 1185665, 48612265, …. (OEIS A006278).
A lehetséges primitív vagy nem primitív derékszögű háromszögek száma, amelyeknek 
a hipotenúzája
 |
 |
 |
(29)
|
 |
 |
 |
(30)
|
(Beiler 1966 elírásának javítása, p. 117, amely szerint ez a képlet csak a nem-primitív megoldások számát adja meg), ahol 
a négyzetek összege függvény. Például négy különböző egész számú háromszög van 65 hipotenuzával, mivel
 |
(31)
|
Az első számok 
, 2, … esetén 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, …. (OEIS A046080). A legkisebb hipoténuszok, amelyeknek 
különböző hármasa van, az 1, 5, 25, 125, 65, 3125, … (OEIS A006339). A következő táblázat azokat a hipoténuszokat adja meg, amelyekhez pontosan 
különböző derékszögű háromszögek léteznek 
, 1, …, 5 esetén.
 |
OEIS | hipoténuszok, amelyekhez  különböző egész számú háromszögek |
| 0 | A004144 | 1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, … |
| 1 | A084645 | 5, 10, 13, 15, 17, 20, 26, 29, 30, 34, 35, … |
| 2 | A084646 | 25, 50, 75, 100, 150, 169, 175, 200, 225, … |
| 2 | A084646 | 25, 50, 75, 100, 150, 169, 175, 200, 225, ……. |
| 3 | A084647 | 125, 250, 375, 500, 750, 875, 1000, 1125, 1375, … |
| 4 | A084648 | 65, 85, 130, 145, 170, 185, 195, 205, 221, 255, … |
| 5 | A084649 | 3125, 6250, 9375, 12500, 18750, 21875, 25000, … |
Ezért azoknak a módoknak az összessége, amelyekkel 
egy derékszögű háromszögnek akár lába, akár hipotenúzája lehet, a következő:
 |
(32)
|
Az 
, 2, … értékek 0, 0, 1, 1, 1, 2, 1, 1, 2, 2, 2, 2, 1, 4, 2, 1, 5, 3, …. (OEIS A046081). A 
legkisebb számok 
, 2, … esetén 
általános derékszögű háromszög oldalai lehetnek: 3, 5, 16, 12, 15, 125, 24, 40, …. (OEIS A006593; Beiler 1966, 114. o.).
Létezik 50 olyan Pitagorasz-hármas, amelynek hipotenzusa 100-nál kisebb, ezek közül az első néhány, növekvő 
szerint rendezve: (3, 4, 5), (6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083, A046084 és A009000).
Ezek közül csak 16 olyan primitív hármas, amelynek hipotenúzája 100-nál kisebb: (3, 4,5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65), (16, 63, 65), (48, 55, 73), (36, 77, 85), (13, 84, 85), (39, 80, 89) és (65, 72, 97) (OEIS A046086, A046087 és A020882).
A 
hipotenzusú hármasok számát jelöljük 
, a 
hipotenzusú hármasok számát jelöljük 
, és a 
-nál kisebb primitív hármasok számát jelöljük 
. Ezután a következő táblázat foglalja össze a 10-es hatványokra vonatkozó értékeket.
 |
OEIS |  ,  , … |
 |
A101929 | 1, 50, 878, 12467, … |
 |
A101930 | 2, 52, 881, 12471, ….. |
 |
A101931 | 1, 16, 158, 1593, … |
Lehmer (1900) bebizonyította, hogy a 
-nél kisebb hipotenuzájú primitív megoldások száma kielégíti
 |
(33)
|
(OEIS A086201).
Az első néhány primitív Pitagorasz-háromszög inradiusai növekvő 
sorrendben a következők: 1, 2, 3, 3, 3, 6, 5, 4, 10, 5, …. (OEIS A014498).
Az egyenlő területű püthagoraszi háromszögek hármasainak előállítására van egy általános módszer. Vegyük a három generátorhalmazt
 |
 |
 |
(34)
|
||
 |
 |
r^2- | |
r^2-s^2 |
(35)
|
 |
 |
 |
(36)
|
||
 |
 |
 |
(37)
|
||
 |
 |
 |
(38)
|
||
 |
 |
 |
(39)
|
Az egyes hármasok által generált derékszögű háromszög (
) közös területe
 |
(40)
|
(Beiler 1966, pp. 126-127). Ennek a függvénynek az egyetlen szélsőértéke a 
pontban fordul elő. Mivel 
esetén 
, a három nem primitív derékszögű háromszög által osztott legkisebb területet 
adja, ami 840-es területet eredményez, és megfelel a (24, 70, 74), (40, 42, 58) és (15, 112, 113) hármasoknak (Beiler 1966, 126. o.).
Az olyan derékszögű háromszögek, amelyek területe egyetlen számjegyből áll, közé tartozik a 
(területe 6) és a 
(területe 666666; Wells 1986, 89. o.).
1643-ban Fermat kihívta Mersenne-t, hogy találjon egy olyan Pitagorasz-hármast, amelynek hipotenúzája és a lábak összege négyzet. Fermat megtalálta a legkisebb ilyen megoldást:
 |
 |
 |
(41)
|
 |
 |
 |
(42)
|
 |
 |
 |
(43)
|
with
 |
 |
 |
(44)
|
 |
 |
 |
(45)
|
Egy kapcsolódó feladat annak meghatározása, hogy egy adott egész szám 
lehet-e egy racionális oldalú derékszögű háromszög területe. Az 1, 2, 3 és 4 egyetlen racionális oldalú derékszögű háromszög területe sem, de az 5 (3/2, 20/3, 41/6), valamint a 6 (3, 4, 5). A feladat megoldása az elliptikus görbét
 |
(46)
|
A megoldás (
, 
, 
) akkor létezik, ha (46)-nak van racionális megoldása, amely esetben
 |
 |
 |
(47)
|
 |
 |
 |
(48)
|
(Koblitz 1993). Nem ismert általános módszer annak meghatározására, hogy van-e megoldás tetszőleges 
esetén, de egy J. Tunnell által 1983-ban kidolgozott technika lehetővé teszi bizonyos értékek kizárását (Cipra 1996).